Book I. Additions. Ch. VI.

The Projection of the Plain-Scale.

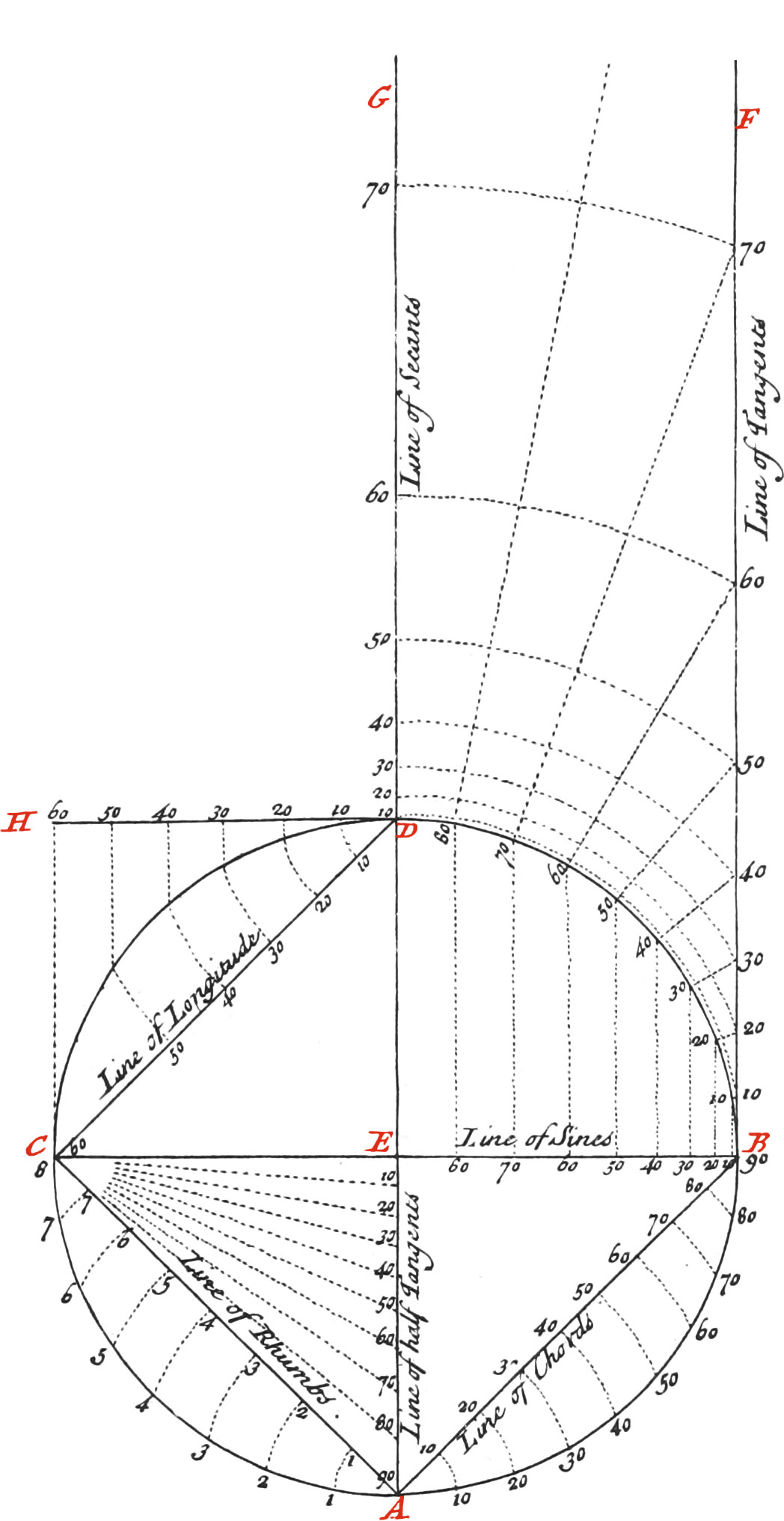
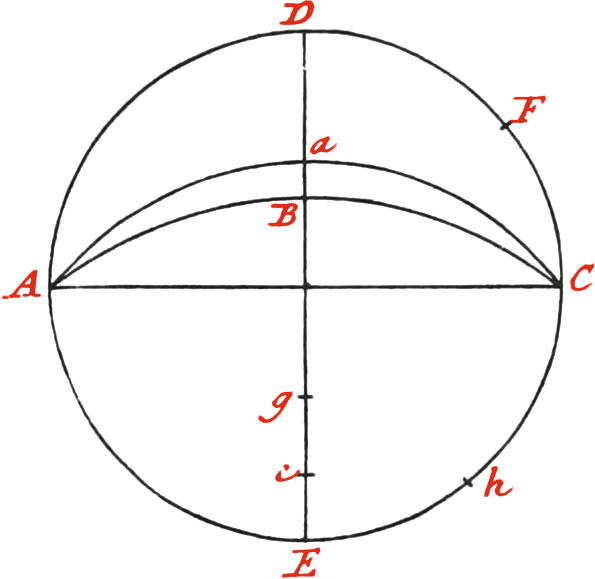
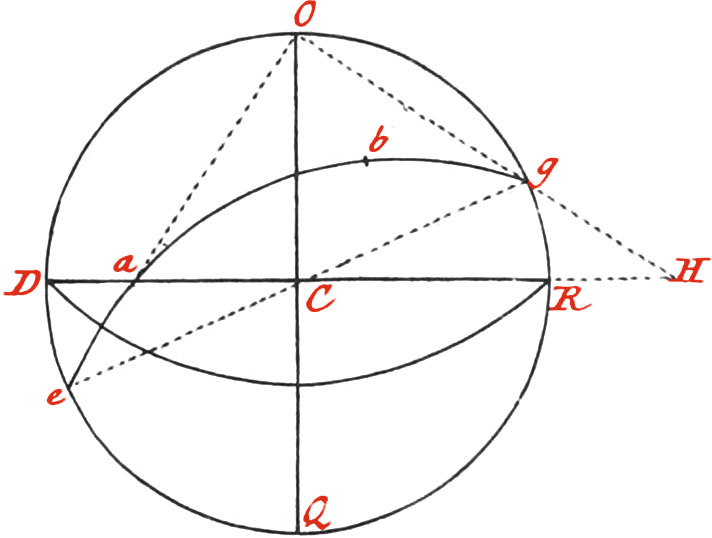
First, draw a Circle ABDC, which cross at right Angles with the Diameters AD, CB; then continue out AD to G, and upon the Point B, raise BF perpendicular to CB. Now draw the Chord AB, and divide the Quadrant AB into 9 equal Tarts, setting the Figures 10, 20, 30, &c. to 90 to them; each of which 9 Parts again subdivide into 10 more equal Parts, and then the Quadrant will be divided into 90 Degrees. Now setting one Foot of your Compasses in the Point A, transfer the said Divisions to the Chord Line AB, and set thereto the Figures 10, 20, 30, &c. and the Line of Chords AB, will be divided, and then may be put upon your Scale, represented in Fig. 6. Now to project the Sines, divide the Arc BD into 90 Degrees, as before you did AB; from every of which Degrees, let fall Perpendiculars on the Semidiameter EB; which Perpendiculars will divide EB into a Line of Sines, to which you must set 10, 20, 30, &c. beginning from the Center, and then you may transfer the Line of Sines to your Scale.

Again, to project the Line of Tangents; from the Center E, and thro’ every Division of the Arc BD, draw right Lines cutting BF, which will divide it into a Line of Tangents, setting thereto the Numbers 10, 20, 30, &c. which you must transfer to your Scale.

To project the Line of Secants, transfer the Distances E 10, E 20, E 30, &c. that is, the Distance from E to 10, 20, 30, &c. on the Tangent Line, upon the Line EG, and setting thereto the Numbers 10, 20, 30, &c. the Line EG will be divided into a Line of Secants, which must be transferred on the Scale.

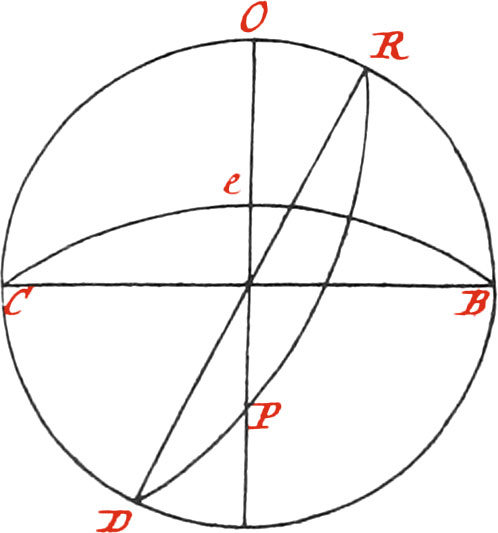
To project the Semi-tangents; draw Lines from the Point C, thro’ every Degree of the Quadrant AB, and they will divide the Diameter AE into a Line of Semi-tangents: but because the Semi-tangents, or Plane-Scales of a Foot in Length, run to 160 Degrees, continue out the Line AE, and draw Lines from the Point C, thro’ the Degrees of the Quadrant CA, cutting the said continued Portion of AE, and you will have a Line of Half-tangents to 160 Degrees, or further, if you please.

Note, The Semi-tangent of any Arc, is but the Tangent of half that Arc, as will easily appear from it’s manner of Projection, and Prop. 20. Lib. 3. Eucl. where it is proved, that an Angle at the Center, is double to one at the Circumference.

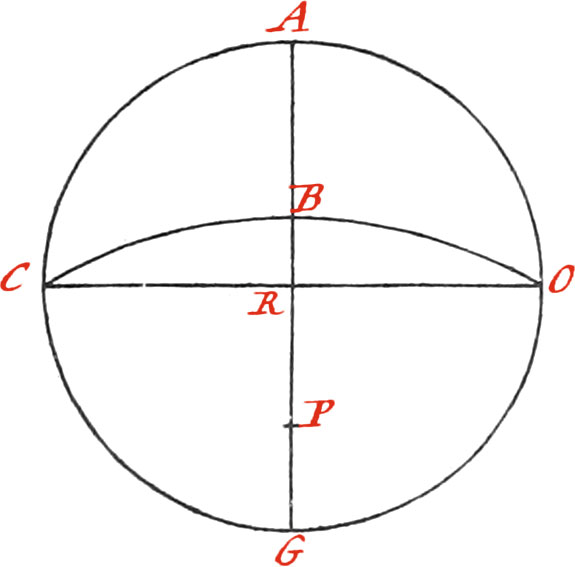
Moreover, to draw the Rhumb-Line; from every 8th part of the Quadrant AC, setting one Foot of your Compasses in A, describe Arcs cutting the Chord AC, which will divide AC into a Line of whole Rhumbs, and in the same Manner may the Subdivisions of half and quarter Rhumbs be made.

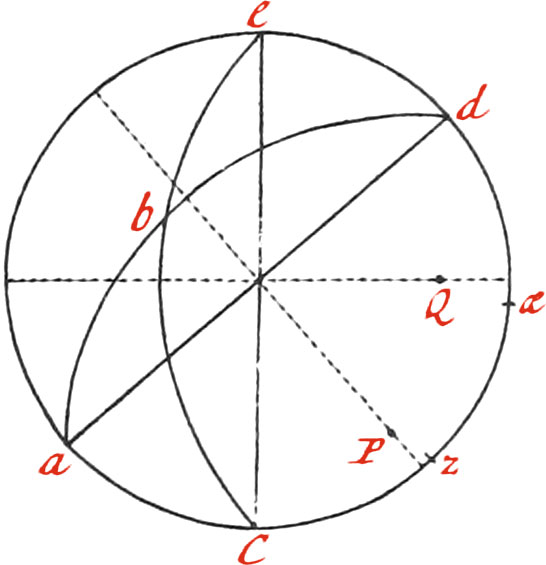
Lastly, to project the Line of Longitude; draw the Line HD, equal and parallel to the Radius CE, which divide into 60 equal Parts (because 60 Miles make a Degree of Longitude under the Equator), every 10 of which Number set Figures to. Now from every of those Parts, let fall Perpendiculars to CE, cutting the Arc CD; and having drawn the Chord CD, with one Foot of your Compasses in D, transfer the Distances from D, to each of the Points in the Arc CD, on the Chord CD, and set thereto the Numbers 10, 20, &c. and the Line of Longitude will be divided.

The Reason of this Construction is, that As Radius is to the Sine Complement of any Latitude, So is the Length of a Degree of Longitude under the Equator; which is 60 Miles, to the Length of a Degree of Longitude in that Latitude.

These being all the Lines commonly put upon the Rulers, called Plain-Scales, excepting equal Parts; therefore I shall proceed to shew their manner of using in Trigonometry, and Spherical Geometry.

But, by the way, note, That Plain-Scales are commonly of these two Lengths, viz. some one foot long, and others, which are put into Cases of Instruments, but half a foot in Length; and on one Side is a Diagonal Scale: they are generally made of Box, and sometimes of Brass or Ivory.

Use I. To make an Angle in the Point A, at the End of the Line AB, of any Number of Degrees, suppose 40.

Take in your Compasses 60 Degrees from the Line of Chords, and letting one Foot in, the Point A, describe the Arc CB; then take 40 Degrees, which is the Number proposed, from the same Line of Chords, and lay them off on the Arc from B to E; draw the Line AE, and the Angle BAE will be 40 Degrees, as is manifest from the Construction of the Line of Chords, and Prop. 15. Lib. 4. Eucl. which shews that the Semidiameter of any Circle, is equal to the Side of a Hexagon inscribed in the same Circle; that is, to the Chord of 60 Degrees.

Use II. The Angle EAB being given, to find the Quantity of Degrees it contains.

Take in your Compasses 60 Degrees from the Line of Chords, and describe the Arc BC; Fig. 7. then take the Extent from B to E in the Compasses; which Extent apply on the Line of Chords, and the Quantity of the Angle will be shewn. This Use, which is only the Reverse of the former, may be likewise done by the Lines of Sines and Tangents, the Method of doing which is enough manifest from Use I.

Use III. The Base of a Triangle being given 40 Leagues, the Angle ABC 36 Degrees, and the Angle BAC 41 Degrees; to make the Triangle, find the Lengths of the Sides AC, CB, and also the other Angle.

Draw the indefinite right Line AD, and take the Extent of 40 Leagues, from the Line Fig. 8. of Leagues, between your Compasses, which lay off upon the said Line from A to B for the Base of the Triangle; at the Points A and B make, by Use I. the Angles ABC, BCA; the first 36 Degrees, and the last 41 Degrees, and the Triangle ACB will be formed; then take in your Compasses the Length of the Side AC, and apply it to the same Scale of Leagues, and you will find it’s Length to be 24 Leagues. Do thus for the other Side BC, and you will find it 27 Leagues and a half; and, by Use II. the Angle ACB will be found 103 Degrees.

By this Use the following Problem in Navigation may be solved, viz. Two Ports, both lying under the same Meridian, being any Number of Miles distant from each other, suppose co, and the Pilot of a Ship, out at Sea on a certain time, finds the Bearing of one of the Ports is SW by S, and the Bearing of the other NW: the Ship’s Distance from each of the Ports at that time is required?

To solve this Problem; draw the right Line AB equal to 3 Inches, or 3 of the largest equal Parts on the Diagonal Scale, which is to represent the 30 Miles, or the Distance from one of the Ports, as A to the other B; at the Point B make an Angle, equal to the bearing Fig. 9. of the Port B from the Ship, which must be 33 Degrees, 45 Minutes; likewise make another Angle at the Point A, equal to the Bearing of the Port A from the Ship, which must be 45 Degrees, then the Point C will be the Place the Ship was in at the time of Observation.

Now to find the Distance of the Ship from the Port A, take the Length of the Side AC in your Compasses, and applying it to the Diagonal Scale, you will find it to be 17\(\frac{1}{10}\) Miles. In the same manner the Distance of the Ship, from the Port B, will be found 21\(\frac{1}{2}\) Miles.

Note, The Reason why the Angles A and B are equal to the Bearing of the Ship from each of those Ports, depends on Prop. 29. lib. 1. Eucl.

Use IV. The base AB of a Triangle being given 60 Leagues, the opposite Angle ACB 108 Degrees, and the Side CB 40 Leagues; to make the said Triangle, and find the Length of the other Side AC.

Draw the Line ab equal to AB, the given Base; and because in any Triangle the Sines of the Sides are proportionable to the Sines of the opposite Angles (as is demonstrated by Trigonometrical Writers), it follows, that As AB is to the Sine of the given Angle C, which is of 72 Degrees, viz. the Complement of 108 Degrees to 180; So is the given Side BC, to the Sine of the Angle CAB: therefore make be equal to the given Side BC of 40 Leagues. Take in your Compasses, upon the Line of Sines, the Sine of 72 Degrees, to which Length make be equal, and draw the Line ac; likewise draw ed parallel to ac, and (by Prop. 4. lib. 6. Eucl.) bd will be the Sine of the Angle CAB, which will be found, by applying it to the Line of Sines, about 39 Degrees: therefore make an Angle at the Point A of 39 Degrees, then take in your Compasses the Length 40 Leagues, and setting one Foot in the Point B, with the other describe an Arc, which will cut the Side AC in the Point C, and consequently the Triangle ABC will be made, and the Length of the Side AC will be found 34 Leagues.

Use V. Concerning the Line of Rhumbs.

The Use of the Line of Rhumbs is only to lay off, or measure, the Angles of a Ship’s Course in Navigation, more expeditiously than can be done by the Line of Chords: As suppose a Ship’s Course is NNE, it is required to lay it down.

Draw the Line AB, representing the Meridian; take 60 Degrees from the Line of Chords, and about the Point A describe the Arc BC. Now because NNE is the third Rhumb from the North, therefore take the third Rhumb in your Compasses, on the Line of Rhumbs, and lay it off upon the Arc from B to C; draw the Line AC, and the Angle BAC will be the Course.

Use VI. Of the Line of Longitude.

The Use of this Line is to find in what Degrees of Latitude a Degree of Longitude is 1, 2, 3, 4, &c. Miles, which is easily done by means of the Line of Chords next to it: for it is only seeing what Degree of the Line of Chords answers to a proposed Number of Miles, and that Degree will be the Latitude, in which a Degree of Longitude is equal to that proposed Number of Miles. As for Example; against 10 Miles, on the Line of Longitude, stand 80 Degrees, and something more; whence in the Latitude of about 80 Degrees, a Degree of Longitude is 10 Miles. Again, 30 Miles on the Line of Longitude, answers to 60 Degrees on the Line of Chords; therefore in the Latitude of 60 Degrees, a Degree of Longitude is 30 Miles. Moreover, against 58 Miles, on the Line of Longitude, stands 15 Degrees of the Line of Chords, which shews that a Degree of Longitude, in the Latitude of 15 Deg. is 58 Miles; and so for others.

Use of the Plain-Scale in Spherical Geometry.

Use I. To find the Pole of any Great Circle.

If the Pole of the Primitive Circle be required, it is it’s Center.

If the Pole of a right or perpendicular Circle be sought, it is 90 Degrees distant, reckoned upon the Limb from the Points, where this Circle, which is a Diameter, cuts it.

If the Pole of an oblique Circle be required,

Consider that this Circle must cut the primitive in two Points, that will be distant from each other just a Diameter, as is the Case of the Intersection of all great Circles.
The Pole of this Circle must be in a right Line, perpendicular to it s Plane.
This Circle’s Pole cannot but lie between the Center of the primitive one, and its own.

Example. Let the Pole of the oblique Circle ABC be required,

Draw the Diameter AC, and then another, as DE, perpendicular to it.
Lay the Edge of your Scale from A to B, it will cut the Limb in F; then take the Chord of 90 Degrees, and let it from F to h.
Lay the Edge of your Scale from h to A, it will cut DE in g, which Point g is the Pole required.

Note, To find the Points F and b, is called reducing B to the primitive Circle and to the Diameter. Also, Note, that every of the primitive Circles in this Use , and the following ones, are supposed to be described from 60 Degrees, taken off from the letter Line or Chords on the Scale.

Use II. To describe a Spherical Angle of any Number of given Degrees.

If the angular Point be at the Center of the primitive Circle, then it is at any plane Angle, numbering the Degrees in the Limb from the Line of Chords; for all Circles passing through the Center, and which are at right Angles with the Limb, must be projected into right Lines.
If the Angle given is to be described at the Periphery of the primitive Circle, draw a Diameter as AC (then take the Secant of the Angle given in your Compasses, and fitting one Foot in A, cross the Diameter in e: or if no Diameter be drawn, placing one Foot in C and crossing the former Arc, you will find the same Point e, which is the Center of the Circle AaC, which, with the primitive Circle, makes the Angle DAa required.

Note, If the Angle given be obtuse, take the Secant of it’s Supplement to 180 Degrees.
If a Point, as a, were assigned, through which the Arc of the Circle constituting the Angle must pass, draw the Diameter AC (as before) then take the Secant of the given Angle, and setting one Foot in A or C, strike an Arc as at e, and then with the Secant of the given Angle, setting one Foot in a, cross the other Arc in e; which will be the Center of the oblique Circle required.

Use III. To draw a great Circle through any two Points given, as a and b, within the primitive one.

Draw a Diameter through that Point which is furthest from the Center, as DR, producing it beyond the Limb if there be Occasion; set 90 Degrees of Chords from D or R, to O, and draw Oa.

Then erect OH perpendicular to a O, and produce it ’till it cuts the Diameter prolonged in H; that Intersection H is a third Point, through which, as also a and b, if a Circle be drawn, it will be a great Circle, eabg.

Which is easily proved, by drawing the Lines eCg; for that Line is a Diameter, because it’s Parts, multiplied into one another, are equal to ac × CH, equal to OC squared. Per Prop. 35. lib. 3. & Coroll. 8. lib. 6. Eucl.

Use IV. To draw a great Circle perpendicular to, or at right Angles to another.

Let it pass through it’s Poles, and it is done.

Of which there will be four Cases:

To draw a Circle perpendicular to the Primitive, which is done by any strait Line passing through the Center.
To draw a Circle perpendicular to a right Circle, is only to draw a Diameter at right Angles with that right Circle.
To draw an oblique Circle perpendicular to a right one, only draw a right Circe that shall pass through both the Poles of such a right Circle.

Thus the oblique Circle DCR is perpendicular to the right one OQ, because it passes through it’s Poles D and R.
To draw an oblique Circle perpendicular to another:

First find F, the Pole of the given oblique Circle CeB, and then draw any-how the Diameter DR: So a Circle, drawn through the three Points D, P, and R, will be the Circle required; for passing through the Poles of the oblique Circle CeB, it must be perpendicular to it.

Use V. To measure the Quantity of the Degrees of any Arc of a great Circle.

If the Arc be part of the Primitive, it is measured on the Line of Chords.
If the Arc be any part of a right Circle, the Degrees of it are measured on the Scale of Semi-Tangents, supposing the Center of the primitive Circle to be in the Beginning of the Scale; so that if the Degrees are to be reckoned from the Center, you must account according to the Order of the Scale of Half-Tangents.

But if the Degrees are to be accounted from the Periphery of the Primitive, as will often happen, then you must begin to account from the End of the Scale of Half-Tangents, calling 80, 10; 70, 20, &c.
To measure any part of an oblique Circle; first find it’s Pole, and there laying the Ruler, reduce the two Extremities of the Arc required to the primitive Circle, and then measure the Distance between those Points on the Line of Chords.

Thus, in the last Figure, if the Quantity of eB, an Arc of the oblique Circle CeB be required, lay a Ruler to P the Pole, and reduce the Points eB to the primitive Circle; so shall the Distance between O and B, measured on the Line of Chords, be the Quantity of Degrees contained in the Arc eB.

Use VI. To measure any Spherical Angle.

If the angular Point be at the Center of the primitive Circle, then the Distance between the Legs taken from the Limb, and measured on the Chords; is the Quantity of the Angle sought.
If the angular Point be at the Periphery, as ACB; here the Poles of both Circles being in the same Diameter, find the Pole of the oblique circle CBO, which let be P; then the Distance of BP, measured on the Scale of Half-Tangents, is the Measure of the Angle ACB.

For the Poles of All Circles must be as far distant from each other, as are the Angles of the Inclinations of their Planes.

But if the two Poles are not in the same Diameter, being both found in their proper Diameter, reduce those Points to the primitive Circle; and then the Distance between them there, accounted on the Line of Chords, is the Quantity of the Angle sought.

When the angular Point is somewhere within the primitive Circle, and yet not at the Center, proceed thus: Suppose the Angle abC be sought; find the Pole P of the Circle abd, and then the Pole of the Circle ebc; after which lay a Ruler to the angular Point, and the two Poles P and Q, and reduce them to the primitive Circle by the Points x and z; So is the Arc xz, measured on the Line of Chords, the Measure of the Angle abC required.

Use VII. To draw a Parallel Circle.

If it be to be drawn parallel to the primitive Circle, at any given Distance, draw it from the Center of the Primitive, with the Complement of that Distance taken from the Scale of Half-Tangents.
If it be to be drawn parallel to a right Circle; as suppose ab, parallel to AB, was to be drawn at 23 Deg. 30 Min. Distance from it; from the Line of Chords take 23 Deg. 30 Min. and set it both-ways on the Limb from A to a, and B to b (or set it’s Complement 66 Deg. 30 Min. both-ways from P the Pole of AB) to the Points a and b.

Then take the Tangent of the Parallel’s Distance from the Pole of the right Circle AB, which is here 66 Deg. 30 Min. and setting one foot in a and b, with the other strike two little Arcs, to intersect each other somewhere above P, which will give C, the Center of the parallel Circle abd required.

If it be drawn parallel to an oblique Circle, and at the Distance suppose of 40 Degrees:

First find P, the Pole of the oblique Circle ABC, and then measure, on the Scale of Half-Tangants, the Distance gP, which suppose to be 34 Degrees; then add to it 50 Degrees, the Complement of the Circle’s Distance, it will make 84 Degrees; and also substracting 50 from it, or it from 50, it will make 16 Degrees: Then this Sum and Difference taken from the Scale of Half-Tangents, and set each way from P the Pole of the oblique Circle, will give the two Extremes ab of the Diameter, or the Points of the Intersection of the Parallel; and then the middle Distance between a and b, is the Center of the true parallel Circle Pab, which is parallel to the given oblique Circle ABC; and at the given Distance of 40 Degrees: or the Half-Tangent of 84, set from g, will give b; and the Half-Tangent of 16 Degrees, set also from g, and the Points a and b, the two Ends of the parallel Circle’s Diameter will be had.

Use VIII. To measure any projected Arc of a Parallel Circle.

If it be parallel to the Primitive, then a Ruler, laid through the Center and the Division of the Limb, will divide the Parallel into the same Degrees, or determine, in the Limb, the Quantity of any Arc parallel to it.
If the Circle be parallel to a right one, as adb is, in case the second of the last Use, and it were required to measure that Arc ab, or to divide it into proper Degrees: Since that parallel Circle is 66 Deg. 30 Min. distant from P, the nearer Pole of the right Circle AB, and consequently 113 Deg. 30 Min. distant from it’s other Pole; take the Half-Tangent of 113 Deg. 30 Min. or the Tangent of it’s half, 56 Deg. 45 Min. and with that Distance, and on the Center of the Primitive, draw a Circle parallel to the Limb; and divide that half of it, which lies towards the opposite Pole of AB, into it’s Degrees: Then a Ruler laid from P, and the equal Divisions of that Semicircle, will divide ab, or measure any part thereof.
To measure or divide the Arc of a Circle which is projected, parallel to an oblique one.

As suppose the Circle ab, which is parallel to the oblique one ABC, Fig. Case 3. of the precedent Use, and at the Distance of 40 Degrees; this parallel Circle being 40 Degrees distant from the Plane of the Circle ABC, must be 50 Degrees distant from it’s Pole, and consequently 130 Degrees from it’s opposite Pole: therefore take the Semi-Tangent of 130 Degrees, or the Tangent of it’s half, 65 Degrees, and with that, as a Radius, draw a Circle parallel to the Limb of the Primitive, which Circle divide into proper Degrees; then shall a Ruler laid through P, and the equal Division of that Circle, cut the little Circle ab into it’s proper Degrees, or truly give the Measure of any part thereof.

These being most of the general Uses of the Scales of Lines commonly put upon Plain-Scales, their particular Applications in Navigation, Spherical Trigonometry, and Astronomy, would take up too much room; therefore I proceed to Gunter’s Scale.

As for it’s Use in the Projection of the Sphere, see the Uses of the English Sector.