Book I. Ch. III.

Of the Construction and Uses of the Protractor.

The Protractor is a Semi-Circle divided into 180 Degrees, or half of 360, which every whole Circle is supposed to be divided into, as was laid in the Definitions.

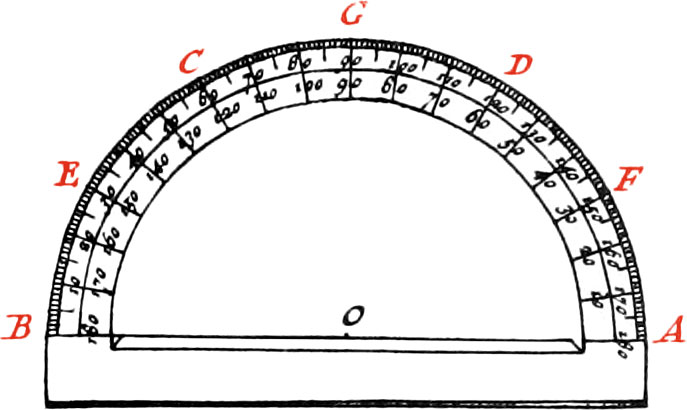
One Side of this Instrument is filed flat, for better applying it on the Paper; and the other Side is sloped; that is, made thin towards the Edge whereon the Divisions are: and for better discovering the Points wherein Angles terminate, there is a small semicircular Notch made in the Center of the Instrument.

How to divide the Limb of the Protractor.

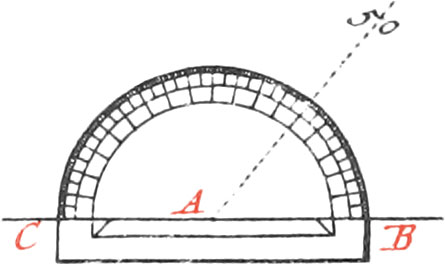
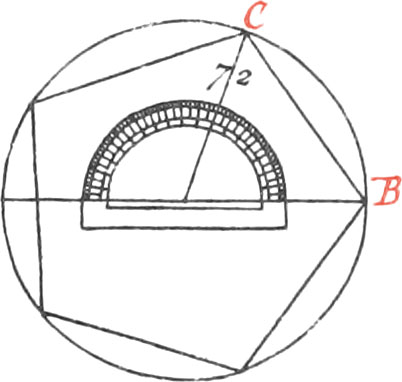
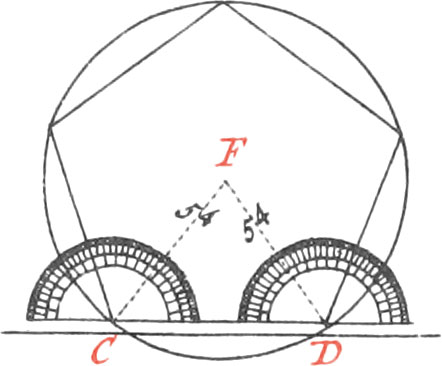
Upon the Line AB, and about the Center O, describe a Semicircle; then carry the Radius AO round the Circumference, which will divide the Semicircle into three equal Parts, in the Points C, D, each of which is 60 Degrees. Again, divide the Arc BC into two equal Parts, in the Point E, and the Arc BE, will be 30 Degrees: then turning this Opening of your Compasses round the Semicircle, it will divide it into six equal Parts. Moreover, divide them again into three equal Parts, and each will be 10 Degrees; and dividing every one of these 10 Degrees into two equal Parts more, Arcs of 5 Degrees will be had. And lastly, in subdividing each of these Arcs of 5 Degrees, into five equal Parts, Arcs of one Degree will be had.

In the same manner may a whole Circle be divided into 360 Degrees, which we shall speak of hereafter.

Note, Protractors are sometimes made of Horn, which, because they are transparent, are commodious enough; but they ought to be kept in a Book when they are not using, because the Horn is apt to wrinkle.

Use I. To make an Angle of any Number of Degrees.

For Example; to make at the Point A, an Angle of 50 Degrees on the Line CAB, lay the Center of the Protractor, marked by a semicircular Cavity, upon the Point A, so that the Diameter of the Semicircle be upon the Line AB; then make a Dot over against the 50th Degree of the Limb of the Protractor, and thro’ it draw a Line to the Point A, which will make an Angle of 50 Degrees with the Line AB.

Use II. The Angle BAD being given, to find how many Degrees it contains.

Lay the Center of the Protractor upon the Point A, and it’s Diameter upon the Line BC; then see what Degree the Line AB cuts the Limb of the Protractor in, which will be the Angle BAD of 50 Degrees.

Use III. To inscribe any regular Polygon in a Circle.

To do this, you must first know how many Degrees the Angle of the Center of each of the regular Polygons contains; which may be found in dividing 360 Degrees, by the Number of Sides of a proposed Polygon: as, for Example, dividing 360 by 5, the Quotient 72, sheweth that the Angle of the Center of a Pentagon is 72 Degrees: again, in dividing 360 by 8, the Quotient 45, gives the Quantity of the Angle of the Center of an Octagon, and so for others.

In knowing the Angle of the Center, the Angle formed by the Sides of the Polygon may likewise be known, in substracting the Angle of the Center of the Polygon from 180 Degrees; as taking 72 Degrees, the Angle of the Center of a Pentagon from 180 Degrees, there remains 108, the Angle of the Polygon. Moreover, taking from 180 Degrees, the Angle of the Center of an Octagon, which is 45 Degrees, there remains 135 Degrees, the Angle of the Octagon.

Therefore to inscribe a Pentagon in a Circle, lay the Center of the Protractor upon the Center of the Circle, and apply the Diameter of the Protractor, to the Diameter of the Circle; then make a Dot against the 72^d Degree of the Limb of the Protractor; and thro’ this Dot, and the Center of the Circle, draw a Line cutting the Circumference of the Circle in the Point C. Now take between your Compasses the Distance of the Points B and C, which will divide the Circumference of the Circle into 5 equal Parts, and drawing 5 right Lines, the Polygon will be made.

If a Heptagon is to be inscribed, divide 360 Degrees by 7, and the Quotient 51\(\frac{3}{7}\)^d sheweth, that the Angle of the Center is almost 51\(\frac{1}{2}\)^d; therefore having placed the Protractor, as before, Note, 51\(\frac{1}{2}\) Degrees on the Limb of the Protractor, thro’ which draw a Line from the Center of the Circle, and you will have the Side of the Heptagon.

Note, Upon some Protractors are placed the Numbers, denoting regular Polygons, to avoid the trouble of Division, in finding the Angles at the Center: as the Number 5, for a Pentagon, is set against 72 Degrees on the Limb of the Protractor; the Number 6 for a Hexagon, is set over-against 60 Degrees, the Number 7 against 51\(\frac{1}{2}\)^d, &c.

Use IV. To describe any regular Polygon upon a given Line.

Let the given Line be CD, upon which it is required to describe a regular Pentagon.

We have shewn in the precedent Use, how to find the Angles of any regular Polygon; and since the Angle made by the two Sides of the Polygon is 108 Degrees, 54 Degrees it’s half will be the Semi-Angle of the Polygon; by means of which, you may describe it in the following manner:

Apply the Diameter of the Protractor to the Line CD, and it's Center to the End D; then make a Dot against the 54th Degree of the Limb, and draw the Line DF, making an Angle of 54^d with the Line CD. Moreover, remove the Center of the Protractor to the other End C, and there likewise make an Angle of 54 Degrees, by drawing the Line CF; then about the Point of Concourse F, describe a Circle with the Distance CF. Lastly, take the Length of the given Line CD, and carry it round the Circumference of the Circle, and drawing four right Lines, the Pentagon will be made.

If an Octagon is to be described upon a given right Line, take half the Angle of the Polygon, which is 67\(\frac{1}{2}\) Degrees, and make an Angle of the like Number of Degrees upon each End of the given Line, by which an Isosceles Triangle will be formed, whole Vertex will be the Center of a Circle, which will be divided into eight equal Parts, by carrying the Compasses round it with the Extent of the given Line.

There may be made many more Operations with the Instruments already spoken of; but we shall content ourselves with those already mentioned, as being the most common, and useful.