Book VI. Additions. Ch. III.

Of Spheres.

Section I. Of the Ptolemaick Sphere.

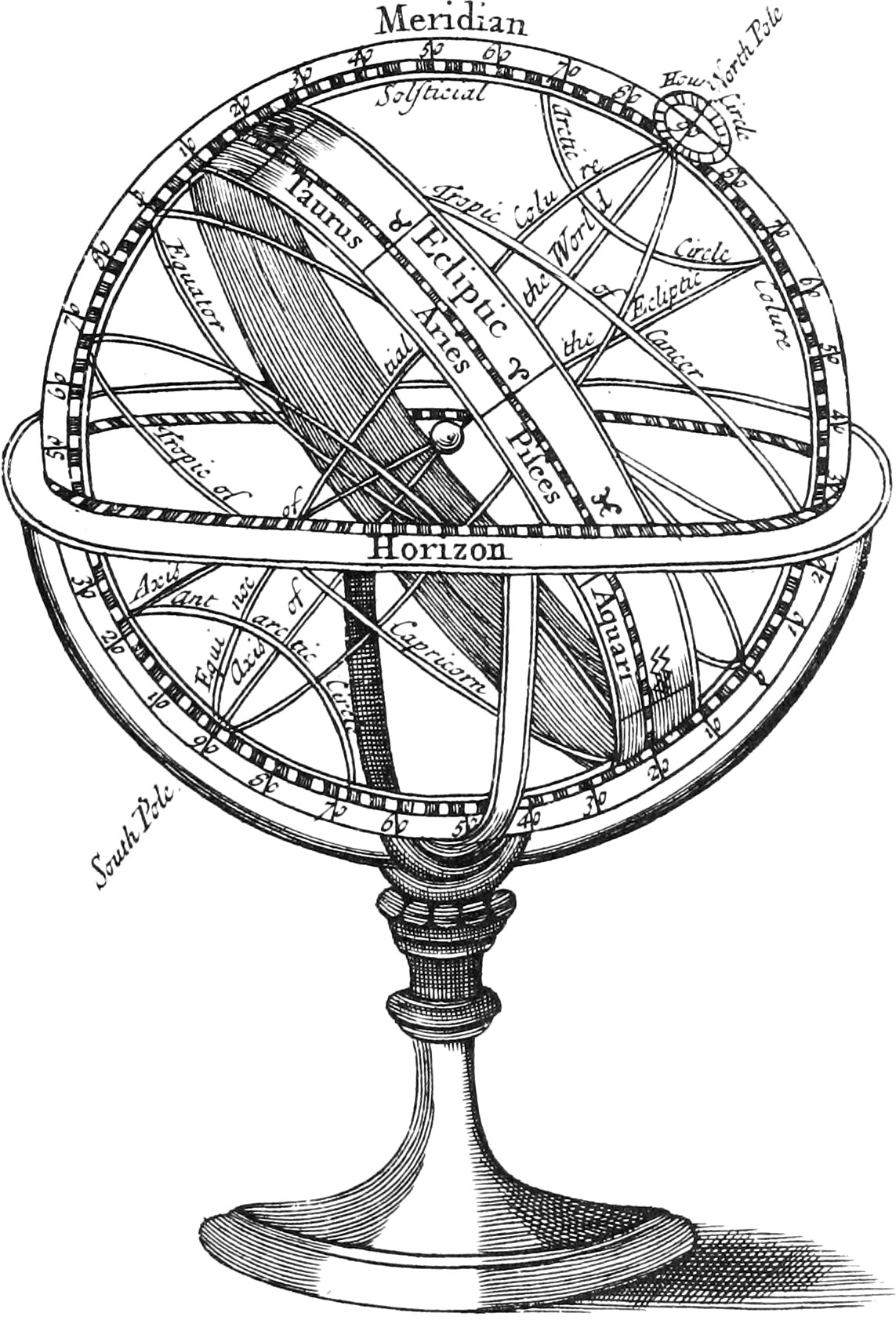
The third Figure represents a Ptolemaick Armillary Sphere, made of Brass, or Wood, confiding of the same Circles that have been described in Chapter I. aforegoing, and having a round Ball fixed in the Middle thereof, upon the Axis of the World, representing the Earth. Upon the Surface of this Ball are drawn Meridians, Parallels, &c. as likewise as many Kingdoms, Countries, Seas, &c. with their Names, as can conveniently be depicted thereon. This Sphere revolves about the said Axis, between the Meridian, and by this means not only shews the Sun’s diurnal and annual Course, &c. about the Earth, according to the Ptolemaick Hypothesis, which supposes the Earth to be at rest, and the Sun to move about the same; but likewise by it any Problem relating to the Sun, may be solved, that can be done by the Globes. And this any one that knows the Use of the Globes may likewise do.

Section II. Of the common Copernican Sphere.

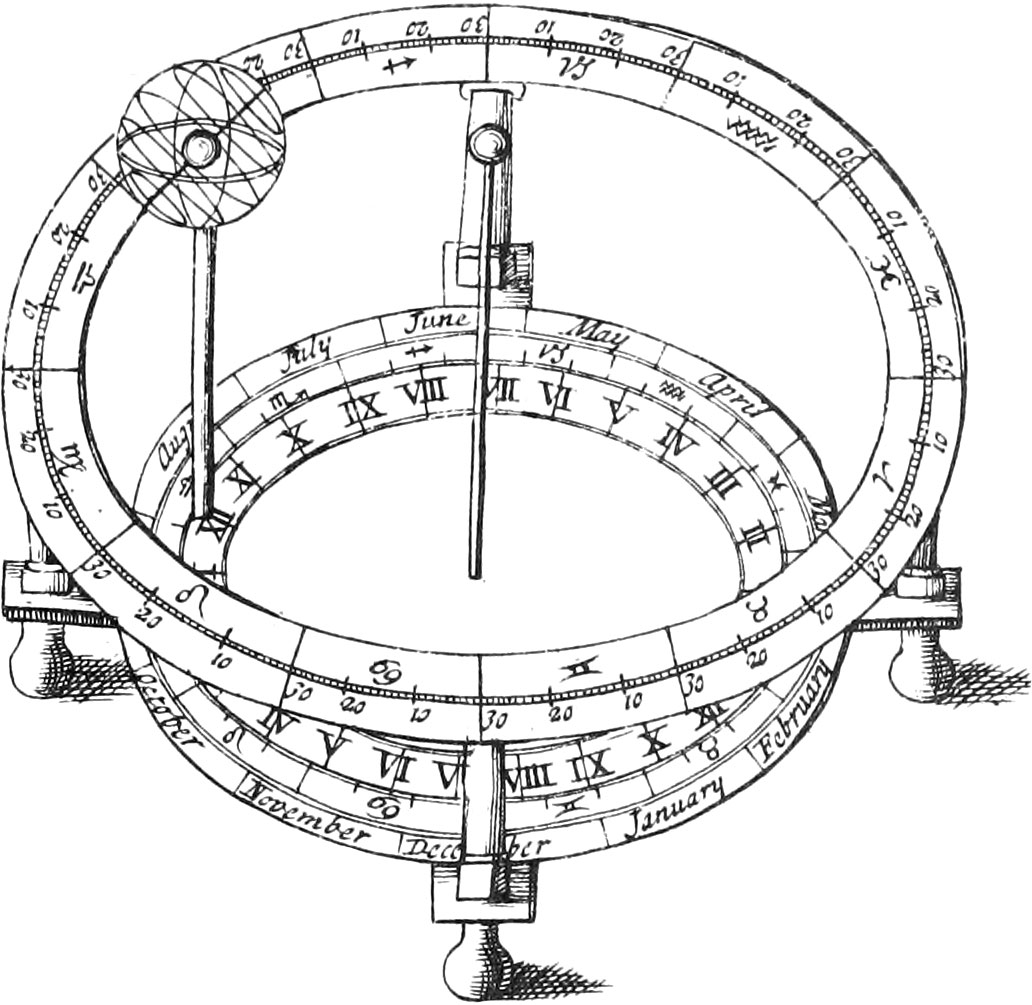
This Sphere stands upon four brass or wooden Feet, upon each of which are fixed the four Ends of a brass or wooden Cross, upon which Cross is fastened a large hollow brass or wooden Circle, whose Center is exactly over the Center of the Cross. Upon the upper Plane of this Circle are the Calendars, and Circle of Signs described, the same as on the Horizon of the Globes. Close within the Inside of this Circle is fitted a flat moveable Rundle, whose Center is common with the Center of the Cross. The outmost Limb of this Rundle is divided into 24 equal Parts, representing the 24 Hours of Day and Night, numbered from the Index (of which more hereafter) towards the Right-hand with Numerical Letters from I to XII, and then beginning again with I, II, &c. to XII again.

There is a round Wheel fixed upon the Cross, under the said Rundle, whose Convex Side is cut into a certain Number of Teeth. Thro’ the Rundle, the Wheel on the Cross, and the Cross itself, is fitted a perpendicular Axis, about which the Rundle moves. This represents part of the Axis of the Ecliptick, and at the Top thereof is placed a little Golden Ball, representing the Sun.

On the under Side of the moveable Rundle moves another Wheel, whose Convex Side is cut into Teeth, and as the Rundle is turned about upon it’s Center, this Wheel is also turned about upon it’s Center, by the falling in of the Teeth on that Wheel fixed on the Cross. Likewise near the outmost Limb of the Rundle is fitted another Wheel, into which is fitted a Pedestal, holding up a Sphere of several Parts, having a Terrestrial Globe inclosed therein, as shall be shewn hereafter. The outmost Limb of this Wheel is likewise cut into Teeth, fitted into the Teeth of the fixed Wheel; and so as the Rundle moves round, this Wheel is carried about, and with it likewise the Earth, and all the Circles fastened upon the aforesaid Pedestal.

On one Side of this Rundle is fastened a little round Pin to turn about the Rundle by, and near this Pin, is an Index upon the Rundle, reaching to the outward Limb of the great hollow Circle, and so at once may be applied to the Day of the Month in both Calendars, and also to the Degree of the Ecliptick the Sun is in that Day at Noon. Note, This Index is called the Index of the moveable Rundle. On each Side of the Cross is placed a Pillar, supporting a broad Circle, representing the Zodiack, with the Ecliptick in the Middle thereof, as in the Ptolemaick Sphere. Note, This is called the Zodiack, in the Use of the Sphere.

Upon the aforesaid Pedestal are fastened two Circles cutting each other at Right Angles, representing the two Colures so placed, that the Points wherein they intersect each other stand directly upwards and downwards, and represent the Poles of the Ecliptick, the uppermost being the North, and the other the South. One of these Colures, viz. the Solstitial, hath a small Hour-Circle placed thereon, at the Extremity of the Axis of the Earth. In the Middle, between the two Poles of the Ecliptick, is a Circle broader than the Colures, cutting them at Right Angles; and this represents the Ecliptick, so called in the Use of the Sphere, and is divided into Degrees, figured with the Names and Characters of the Signs, and having on the inward Edge thereof several of the most notable fixed Stars, with the Names affixed to them, and each Star placed to the Degree and Minute of Longitude thereon, that it hath in Heaven.

Oblique to this Ecliptick 23\(\frac{1}{2}\) Degrees, on the Inside, is fitted a thin Circle, representing the Equinoctial, and is divided into 360 Degrees, and having two parallel lesser Circles at 23\(\frac{1}{2}\) Degrees equally distant therefrom, representing the Tropicks. On the Inside of all these Circles, two thin Semi-Circles (called Semi-Circles of Latitude) are fitted in the Poles of the Ecliptick, so as one of them may move thro’ one half the Ecliptick, viz. from Cancer thro’ Aries to Capricorn; and the other from Cancer thro’ Libra to Capricorn: the former of these may be called the vernal Semi-Circle of Latitude, and the other the autumnal Semi-Circle of Latitude. On the Edge of these Semi-Circles are depicted the same fixed Stars in their proper Longitude and Latitude, as are placed on the Ecliptick Circle aforesaid, with their several Names affixed to them.

Thro’ the solstitial Colure at 23\(\frac{1}{2}\) Degrees from each Pole of the Ecliptick, goes a Wire, representing the Earth’s Axis, having an Index placed on the End thereof, for pointing at the Hour, on the Hour-Circle placed on the solstitial Colure, as aforesaid. In the Middle of this Axis is fixed a round Ball, representing the Earth, having Meridians, Parallels, &c. and the Bounds of the Lands and Waters depicted thereon, as also the Names of as many Countries and Towns as can be placed with conveniency thereon. And in two opposite Points of the Equinoctial of this Ball, viz. 90 Degrees distant from the first Meridian, are fixed two small Pins, whereon a moveable Horizon is placed, in the East and West Points thereof; so that these Pins serve for an Axis to the Horizon: for on these Pins the Horizon may be elevated or depressed to any Degree the Pole is elevated above the Horizon. This Horizon slides on the North and South Points, within a brazen Meridian, hung upon the Axis of the Earth.

Round this Meridian, on the outmost Side, is made a Groove, having a small brass Ring fitted therein, so as the upper Side thereof is even with the upper Side of the brazen Meridian. This small brass Ring is fastened to two opposite Points in the Horizon, viz. in the North and South, and serves as a Spring to keep it to the Degree of the Meridian you elevate the Horizon to. Upon two Pins on this small Ring, are likewise fastened two Semi-Circles of Altitude, yet not so fastened, but that they may move as upon Centers, the one moving from North to South, thro’ the East-Side of the Horizon, and the other the same way thro’ the West-Side. This Motion is performed upon the two Pins aforesaid, as upon two Poles, which they represent, viz. the Poles of the Horizon, and therefore are so placed, that they may divide the upper and lower half of the Horizon into two equal Parts, and as the Horizon is moved, slide always into the Zenith and Nadir, and so become the Poles of the Horizon. These two Semi-Circles of Altitude are divided into twice 90 Degrees, numbered at the Horizon upwards and downwards, and ending at 90 in the Zenith and Nadir.

Section III. The Use of the Copernican Sphere.

Use I. The Day of the Month given; to rectify the Sphere for Use in any given Latitude, and to set it correspondent to the Situation of the Heavens.

Bring the Index of the moveable Rundle to the Day of the Month, and elevate the Horizon to the Latitude of the Place; then bring the Meridian to the Sun’s Place in the Ecliptick, and the Index of the Hour-Circle to 12. Lastly, Bring the Center of the Earth, the Sun, or Golden Ball, in the Sphere, and the Sun in Heaven into a Right Line. Then will the Earth be rectified to it’s Place in Heaven, the Horizon to it’s Latitude on Earth, the Circles on the Sphere agreeable to those in Heaven, and the whole correspondent with the Heavens for that Day at Noon.

Use II. The Day of the Month being given, to find the Sun’s Declination.

Rectify the Earth’s Place (according to Use I.) and then you will have the Sun’s Place in the Zodiack; then bring the Meridian to the Sun’s Place in the Ecliptick on the Sphere; and the Number of Degrees comprehended between the Equinodial and the Sun’s Place, are the Sun’s Declination for that Day at Noon.

Use III. To find the Sun’s Right or Oblique Ascension for any Day at Noon.

Rectify the Earth’s place to the Day of the Month, and bring the Meridian to the Sun’s place in the Ecliptick; and the Number of Degrees on the Equinoctial contained between the vernal Colure, and the Sun’s place, are the Right Ascension sought.

Now to find the Oblique Ascension, turn the Earth ’till the East side of the Horizon stands against the Sun, and the Degree of the Equinoctial then at the Horizon, shews the Oblique Ascension.

Use IV. To find the Sun’s Meridian Altitude.

Bring the Index of the Rundle to the Day of the Month, and rectify the Horizon to the Latitude of the Place. This being done, bring the Meridian to the Sun’s place in the Ecliptick, and the Number of Degrees on the Meridian comprehended between the Horizon and the Sun’s place, gives the Meridian Altitude sought.

Use V. To find the Sun’s Altitude at any time of the Day.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon, and Hour-Index: then turn the Earth ’till the Hour-Index comes to the given Hour of the Day, and bring the vertical Circle to the Sun’s place, and the Number of Degrees of the vertical Circle that transite the Sun’s place, are his Altitude above the Horizon.

Use VI. The Sun’s Altitude being given, to find the Hour of the Day.

Bring the Index of the Rundle to the Day of the Month, and rectify the Horizon and Hour-Index (as by Use I.); then turn the Earth ’till the you can fit the Horizon to the given Altitude upon the vertical Circle, directly against the Sun’s place; then the Hour-Index will give the Hour of the Day, respect being had to the Morning or Afternoon.

Use VII. To find at what Hour the Sun comes to the East or West Points of the Horizon.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index (as by Use I.).; then bring the vertical Circle to the East Point of the Horizon, if it be the Sun’s Easting you enquire; or to the West Point of the Horizon, if it be the Sun’s Westing. This being done, turn the Earth ’till the vertical Circle comes to the Sun’s place; then will the Index point to the Hour of the Day.

Use VIII. To find the time of the Sun’s rising or setting.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon, and Hour-Index, Then turn the Earth Eastwards, ’till some part of the East-side of the Horizon stands directly against the Sun’s place; then will the Hour-Index point to the time of the Sun’s rising. Again, Turn the Earth ’till some part of the West-side of the Horizon stands directly against the Sun’s place, then the Index of the Hour-Circle will shew the time of the Sun’s letting.

Use IX. The Hour of the Day given, to find the Sun’s Azimuth.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index. Then turn the Earth ’till the Hour-Index points to the Hour of the Day given. This being done, bring the vertical Circle to the Sun’s place, and the Number of Degrees of the Horizon, that the vertical Circle cuts, counted from the East Point, either Northwards or Southwards, are the Degrees of the Sun’s Azimuth before Noon. Or the Number of Degrees of the Horizon that the vertical Circle cuts, counted from the West-side of the Horizon, either Northwards or Southwards, give the Sun’s Azimuth after Noon.

Use X. To find in what Place of the Earth the Sun is in the Zenith, at any given time; as also in what several Places of the Earth the Sun shall stand in the Horizon at the same time.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Hour-Index; then seek the Sun’s Declination, and turn the Earth eastwards ’till the Index points to the given Hour; so shall the Number of Degrees of the Equinoctial that the Meridian passes thro’ while the Earth is thus turning, be the Number of Degrees of Longitude, eastwards from your Habitation, the Place shall have in the Parallel of the Sun’s Declination.

Now if you open a Pair of Calliper Compasses to 90 Degrees on the Equinoctial, and place one Foot in this Point of the Earth thus found, and turn the other Foot round about the Earth, all the Places that the Foot passes thro’ will at that time have the Sun in their Horizon.

Use XI. How to find the true Places of the Stars on the Sphere; as likewise their Longitude and Latitude.

Round the Plane of the Ecliptick, are placed several of the most noted fixed Stars, according to their true Longitude; and along the two Semi-circles of Latitude, are the same Stars placed according to their Latitude from the Ecliptick. Whence if you would find the true place of any given Star in the Sphere; First seek the Star in the Ecliptick, and likewise the same Star on one of the Semi-circles of Latitude, and bring the edge of that Semi-circle to the Star in the Ecliptick; then will the Star on the Semi-circle of Latitude stand in the same Place and Situation on the Sphere, that it does in Heaven.

Use XII. To find the Declination, right and oblique Ascension of a Star.

Bring the proper Semi-circle of Latitude to the Star on the Ecliptick, and the Meridian to the Star on the Semi-circle of Latitude; and then the Number of Degrees on the Meridian, comprehended between the Equinoctial and the Star, are its Declination. Likewise the Decree of the Equator, cut by the Meridian, is the Star’s right Ascension. But to find a Star’s oblique Ascension, rectify the Horizon (as by Use 1.) and bring the proper Semi-circle of Latitude to the Star in the Ecliptick, and turn the East-side of the Horizon to the Star; then will the Degree of the Equator cut by the Horizon be the Star’s oblique Ascension.

Use XIII. To find the Time of the Rising and Setting of any Star in any given Latitude.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour Index; then bring the proper Semi-circle of Latitude to the Star on the Ecliptick, and the East-side of the Horizon to the Star; this being done, the Hour-Index will shew the Hour the Star rises at: and if you bring the West-side of the Horizon to the Star, the Index of the Hour-Circle will shew the Time that the Star sets.

Use XIV. The Day of the Month, Hour of the Night, and Latitude of the Place being given, to know any remarkable Star observed in the Heavens.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index; then turn the Earth ’till the Index of the Hour-Circle comes to the Hour of the Night, and observe the Altitude of the Star, and what Point of the Compass it bears upon. Afterwards bring the vertical Circle to the same Point of the Compass, and number the Star’s Altitude on the vertical Circle, and try with the Semi-circle of Latitude what Star you can fit to that Altitude, for that is the Star in the Heavens.

Use V. The Azimuth of any known Star being given, to find the Hour of the Night, and Almicanter of that Star.

Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index; afterwards bring the Star to its place, and the vertical Circle to its known Degree of Azimuth. This being done, turn the Earth ’till the vertical Circle comes to the Star; then the Index of the Hour-Circle will shew the Hour of the Night, and the Degree of the vertical Circle cut by the Star will be its Almicanter.

Section IV. The Description and Use of the Copernican Sphere, called the Orrery.

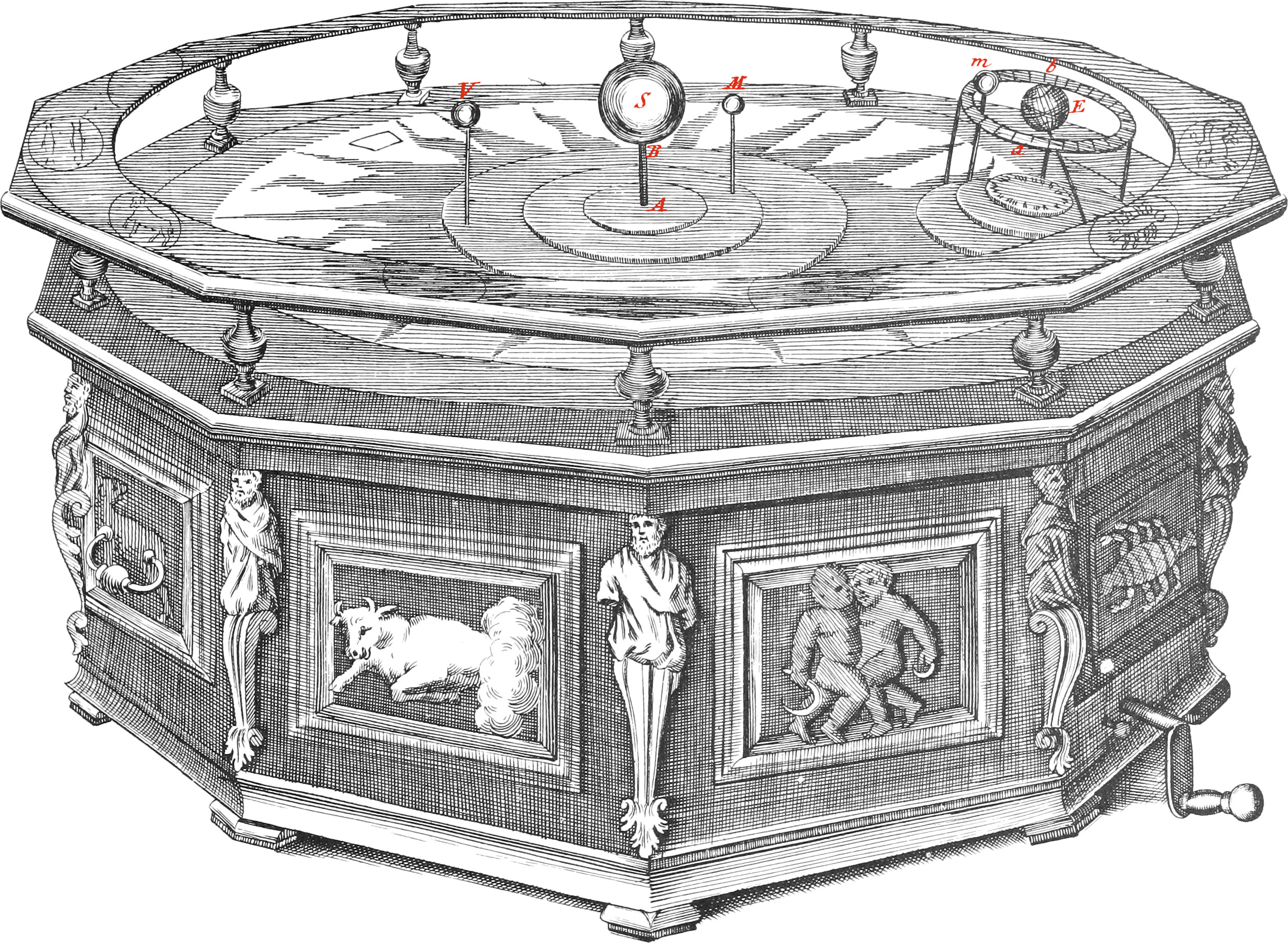
The Outside of this Instrument, as appears by the figure thereof, is very beautiful, the Frame being of fine Ebony adorned with 12 Silver Pilasters, in the form of Caryatides; and with all the Signs of the Zodiack cast of the same Metal, and placed between them: the Handles are also of Silver finely wrought, with very nice Joints. On the top of the Frame, which is exactly circular, is a broad Silver Ring, on which the Figures of the twelve Signs are exactly graved, with two Circles accurately divided; one shewing the Degrees of each Sign, and the other the Sun’s Declination against his place in the Ecliptick each Day at Noon.

The aforesaid Silver Plate, represents the Plane of the great Ecliptick of the Heavens, or that of the Earth’s annual Orbit round the Sun; which, as it passes thro’ the Center of the Sun, so its Circumference is made by the Motion of the Earth’s Center; and which, for the better advantage of View and Sight, is in the Figure placed parallel to the Horizon.

S is a large gilded Ball, standing up in the middle, whose Support AB makes with the Plane of the Ecliptick an Angle of about 82 Degrees. This Support represents the Sun’s Axis continued, about which he revolves in about 25 Days, and the Golden Ball represents the Sun itself placed pretty near the Center of the Earth’s Orbit; so that when the Instrument is set a-going, the Excentricity of the Earth, and the other Planets, may be in the same Proportion as they are in the Heavens.

The two little Balls M and V, which stand upon two Wires at different Distances from the Sun, represent Mercury and Venus: The reason why they are placed upon the said two Wires, is only that their Centers may be sometimes in, and always pretty near the Plane of the great Ecliptick; and this Position is contrived in order to shew what Appearances they do really exhibit in their several Revolutions round the Sun.

The Globe E is of Ivory, and represents the Earth. The Pin or Wire that supports it, represents the Earth’s Axis continued, and makes an Angle of 66\(\frac{1}{2}\) Degrees, with the Plane of the Ecliptick. And as the Earth in each of her annual Revolutions round the Sun, always keeps her own Axis parallel to itself; so when this Instrument is set a-going, the little Ivory Earth will likewise do so too, in it’s Revolution round the Golden Sun S.

The little Ball m standing upon a Wire, represents the Moon, and ab is a Silver Circle representing her Orbit round about the Earth, the Plane whereof always passes thro’ the Center of the Earth; and there are several Figures graved upon it, shewing the Moon’s Age, from one New Moon to the other.

One half of the Moon’s Globe is white, and the other black, that so her Phases may be represented: for this Instrument is so contrived, that this little Moon will turn round it’s own Axis, at the same time as it moves in the Silver Orbit round the Earth E.

The whole Movement, which consists of near 100 Wheels, is covered by a great Brass Plate, having a Hole in it, and there is a moveable Index on the Silver Ecliptick, on the former of which, are the common Solar Years denoted; and by taking the Instrument to pieces, it may be set to this present time; and the Planets, by means of an Ephemeris, may be set to any particular time also. So that if a Weight or Spring, as in a Clock, were applied to the Axis of the Movement, so as to make it move round once in just twenty-four Hours, the representative Planets in the Instrument, viz. Mercury, Venus, the Earth, and the Moon, would all perform their Motions round the Sun, and one another, exactly in the same Order as their Originals do in the Heavens; and so the Aspects, Eclipses, &c. of the Sun and Planets, would thereby be shewn for ever. But because this would be instructive only in that slow and tedious way, to such as could have daily recourse to it, therefore there is a Handle fitted to it, by which the Axis may be swiftly turned round; and so all the Appearances shewn in a very little time: for by turning the Handle backwards or forwards, what Eclipses, Transits, &c. have happened in any time past, or what will happen for any time to come, will be shewn, without doing any injury to the Instrument.

One entire Turn of the Handle of this Instrument, answers to the diurnal Motion of the Earth about it’s Axis, and is measured by means of an Hour-Index, placed at the Foot of the Wire whereon the Earth is fixed, moving once round in the same time. Also observe that the Contrivance of this Instrument is such, that the Motion may be made to tend either way, forwards or backwards; and so the Handle may be turned about ’till the Earth be brought to any Degree or Point of the Ecliptick required.

Again, As the Earth moves round, by turning the Handle, the Moon’s Orbit rises and falls about 5 Degrees above and below the great Ecliptick, that so her North or South Latitude may be exactly represented; and there are two little Studs placed in two opposite Points of the Moon’s Orbit, representing the Moon’s Nodes.

Now if the Handle, one Turn of which answers to one Natural Day, or twenty-four Hours, be turned twenty-five times about, then the Sun will have moved once round about it’s Axis. Again, 365\(\frac{1}{4}\) of the Turns of the Handle will carry the Earth quite round the Sun; 88 will carry Mercury quite round; 244 will make Venus move once round the Sun; and about 27\(\frac{1}{4}\) Turns will carry the Moon round the Earth in her Orbit, which will likewise at the same time always turn the same Hemisphere towards the Earth.

And by thus revolving the Earth and Planets round the Sun, the Instrument may be brought to exhibit Mercury, and sometimes Venus, as directly interposed between the Earth and the Sun; and then they will appear as Spots in the Sun’s Disk: and this Instrument shews also very clearly the Difference between the Geocentrick and Heliocentrick Aspects, according as the Eye is placed in the Center of the Earth or Sun.

This Instrument likewise very plainly shews the Difference between the Moon’s Periodick and Synodick Months, and the reason thereof; for if the Earth be set to the first Point of Aries, at which time suppose the first New Moon happens, and afterwards the Handle be turned 27\(\frac{1}{4}\) times about, we shall have the second New Moon; and if at the Earth’s Place in the Ecliptick where this last New Moon happens, some Mark be made, and then the Handle be turned 27\(\frac{1}{4}\) times more, the Moon will be exactly brought again to interpose between the Earth and the Sun, that is, it will be New Moon with us: but the Line of the Syzygy will not be right against the aforesaid Mark in the Ecliptick, but behind it; and it will require two Days time, or two Turns more of the Handle, before it gets thither. The reason of this is plain, because in this 27\(\frac{1}{4}\) Days, the Earth advances so far forwards in her annual Course, as is the Quantity of the Difference in time between the Moon’s two Months.

If the Handle be turned about ’till the Conjunction or Opposition of the Sun and Moon happens in or near the Nodes, then there will be an Eclipse of the Sun or Moon. But in order yet further to shew the Solar Eclipses, and also the several Seasons of the Year, the Increase and Decrease of Day and Night, and the different Lengths of each in different Parts of our Earth, there is a little Lamp contrived to put on upon the Body of the Sun, which carting, by means of a Convex Glass (the Room wherein the Instrument is, being a little darkened), a strong Light upon the Earth, will shew at once all these things: First, how one half of our Globe is always illuminated by the Sun, while the other Hemisphere is in the dark, and consequently how Day and Night are formed by the Revolution of the Earth round her Axis. Also by turning round the Handle, you will see how the Shadow of the Moon’s Body will cover some part of the Earth, and thereby shew, that to the Inhabitants of that part of the Earth there will be a Solar Eclipse.

When the Earth is brought to the first Degree of Aries or Libra, the reason of the Equality of Days and Nights all over the Earth, will be plainly shewn by this Instrument; for in these Positions, as the Earth turns about her Axis, just one half of the Equator, and all Parallels thereto, will be in the Light, and the other half in the Dark; and therefore the Days and Nights must be every where equal: for the Horizon of the Earth’s Disk will be parallel to the Plane of the Solstitial Colure.

And when the Earth is brought to Cancer, the Horizon of the Disk, or that Plane which divides the Earth’s enlightened Hemisphere from the darkened one, will not then be parallel to, but lie at Right Angles to the Plane of the Solstitial Colure. The Earth being now in Cancer, the Sun will appear to be in Capricorn, and consequently it will be our Winter Solstice. And as the Earth is turned either way about it’s Axis, the entire Northern frigid Zone, or all Parts of the Earth lying within the Artick Circle, are in the dark Hemisphere; and by making a Mark in any given Parallel, by the Earth’s diurnal Revolution, you will know how much longer the Nights are than the Days in that Parallel. And the contrary of this will happen, when the Earth is brought to Capricorn.

Therefore this Instrument delightfully and demonstratively shews, how thereby all the Phænomena of the different Seasons of the Year, and the Varieties and Vicissitudes of Night and Day, are solved and accounted for.