Book VIII. Ch. VII.

Of the Construction of a Water-Clock.

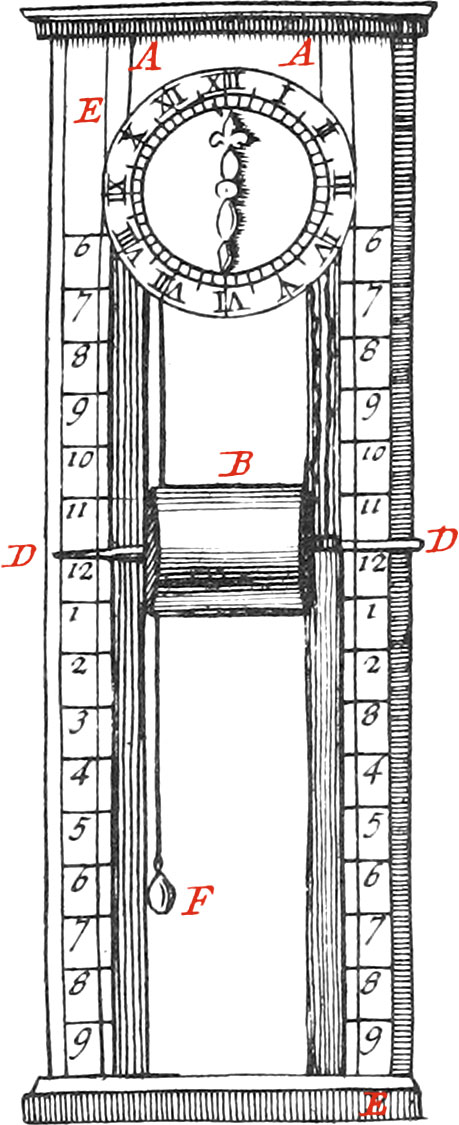
This Clock is composed of a Metalline well soldered Cylinder, or round Box B, wherein is a certain Quantity of prepared Water, and several little Cells, which communicate with each other by Holes near the Circumference, and which let no more Water run thro’ them than is necessary for making the Cylinder descend slowly by it’s proper Weight. This Cylinder is hung to the Points AA by two fine Cords of equal Thickness, which are wound about the Iron Axle-Tree DD, which Axle-Tree goes thro’ the exact middle of the Cylinder at right Angles to the Bases, and as it descends shews the Hour marked upon a vertical Plane on both sides of the Cylinder. The Divisions on this Plane are made thus: Having wound up the Cylinder to the top of the Plane from whence you would begin the Hour-Divisions, let it descend 12 Hours, reckoned by a Clock or good Sun-Dial, and note the Place where the Axle-Tree is come to at the End of that Time, and divide the Space the Axle-Tree has moved thro’ in 12 equal Parts, each of which set Numbers to, for the Hours.

We make likewise Clocks of this kind, that shew the Hour by a Hand turning about a Dial-Plate, as appears in the same Figure. This is done by means of a Pulley four or five Inches in diameter, fastened behind the Dial-Plate on a Brass or Steel Rod, going thro’ the Center thereof; one End of this Rod goes into a little Hole for supporting it, and at the other End is fixed the Hand shewing the Hour.

The said Hand turns by means of a Cord put about the Pulley, one end of which supports the Axle-Tree at the Place H, and at the other end is hung a small Weight F; then as the Cylinder slowly descends, it causes the Pulley to turn about, and consequently the Hand, which by this means shews the Hour.

The Circumference of the Pulley must be equal to the Length the Axle-Tree of the Cylinder moves thro’ during twelve Hours; and for this End you must take that Length exactly with a String, and then make the Circumference of the Pulley equal to the Length of the String; and so the Pulley and Hand will go once round in twelve Hours. When the Cylinder descends a little too swift, and consequently the Hand moves too fast, then the Weight F must be made heavier; and when it descends too slow, it must be made lighter.

The Construction of the Cylinder or Round Box.

This Cylinder is sometimes made of beaten Silver, but commonly with Tin. The Diameter of each Base thereof is about 5 Inches, and the Height 2.

The Inside of this Cylinder is divided into seven little Cells (and sometimes into five), as the Figure shews. These little Cells are made by soldering seven Silver or Tin inclined Planes to each Base, and the concave Circumference of the Cylinder; each of which are about 2 Inches long, as BF, AL, EI, DH, CG. These Cells have such an Inclination when they turn about, that they receive the Water thro’ a little Hole in each Plane near the Circumference, and by this means let it run from one Cell to the other; so that as the Cylinder rolls, it descends, and shews the Hour upon a vertical Plane by the Extremity of the Axle-Tree, which (as we have said) goes thro’ the square Hole M in the middle of the Cylinder. Note, In a Cylinder of the abovesaid bigness we usually pour seven or eight Ounces of distilled Water. But before the Water be poured in, you must take great care to well solder the inclined Planes to the Bases and Circumference. After this, the Water must be poured thro’ two Holes posited on one and the same Diameter, equally distant from the Center M; then these Holes must be well stopped with soldering, that so the Air may not get in, or the Water run out while the Cylinder is turning about.

You may perceive, by the Figure, that the inclined Planes within the Cylinder do not join each other, but end in G, H, I, L, F, that so when the Cylinder is winding up, the Water may run swiftly from one Cell to the other, and the Cylinder remain at any Height one pleases; because that at every Motion we give it when winding up, the Water running in a great Quantity thro’ the Openings, the Cylinder will presently assume it’s Equilibrium, which would not happen if the Cells were absolutely inclosed: for the little Holes in the inclined Planes, are not sufficient for letting the Water run thro’ them so swift as it ought, it going through them but by drops.

It is manifest, if this Cylinder was suspended by the Center of Gravity thereof, as would happen if the Surface of the Axle-Tree should exactly pass thro’ the Center of the said Cylinder, it would remain at rest; and the Cause of it’s Motion is, that it is suspended without the Center of Gravity by the Cord’s going about the Axle-Tree, which ought not to be, with regard to the bigness of the Cylinder, and the Quantity of Water in it, but about one Line, or one Line and a half, in thickness.

From what has been said it is evident, that the Swiftness or Slowness of the Motion of the Cylinder depends upon the Thickness of the Axle-Tree; for the thicker the Axle-Tree is, the slower will the Cylinder descend, and contrariwise, because it has more or less Excentricity, and consequently the Water will run more or less swift from one Cell to another; by which means the Force of it’s Motion will be more or less ballanced by the Weight of the Water contained in the opposite Cell.

If you have a mind to see the Circulation of the Water in one of these Cylinders, you may have one made that shall have a Glass Base; but then it will be difficult to find a Matter that shall make the inclined Planes stick firm to this Glass Case, and this to the Circumference of the Cylinder.

When the Cylinder is nearly descended to the Bottom of the Cords, you must raise it up with your Hand, making it turn at the same time, so that the Cords may equally roll all along the Axle-Tree, and that it be hung horizontally.

I have hinted before, that the Water poured into the Cylinder must be distilled, otherwise it must be often changed, because it makes a Slime about the small Holes thro’ which it runs, which hinders it’s running as it should do.