Suppl. Ch. I.

Of Instruments for drawing or copying of Draughts, and making the Pictures of Objects.

I. One of the best Kind of Parallelograms for drawing.

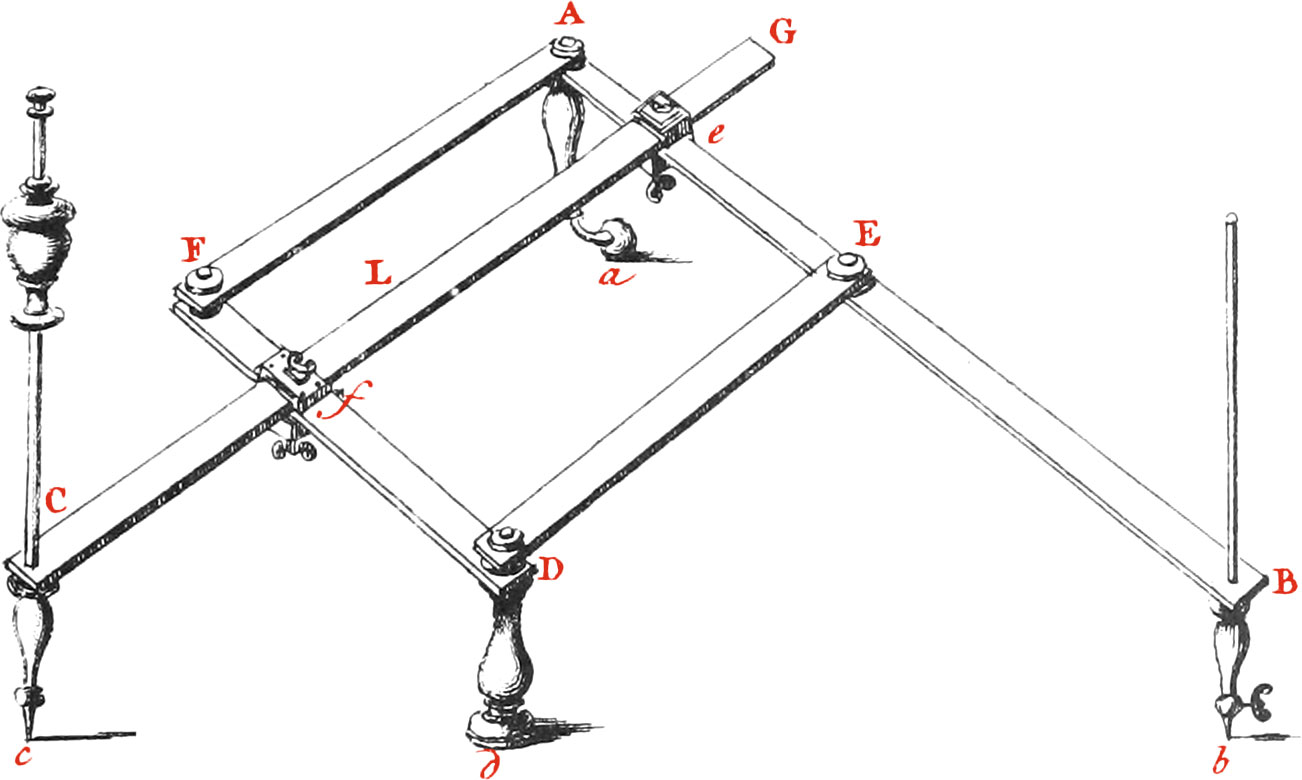
This Instrument (Fig. 1.) usually made of Brass or Wood, consists of four Rulers; the longest one AB being about 20 Inches in Length, so fastened together at the Places A, F, D, E, that the Parallelogram AFDE may vary it’s Species, while the Sides remain the same, that is, that any two adjacent Sides may make all variety of Angles from 180 to no Degrees. Upon the opposite Sides, AE, DF are fixed two sliding Sockets e, f; in these Sockets likewise goes the Ruler GC, a little longer than AB; these Sockets may be fastened to any parts of the Sides AE, FD, by means of Screws underneath, and the Ruler GC may be fastened in them by two Screws a top, so as to be always parallel to the Sides AF, ED; which opposite Sides AF, ED are each in Length equal to EB. But the Sides AE, FD, are each a little longer, viz. by twice the width of the Sockets, so that when the Sockets are shoved home to the Side AF, the Distance from the Middle of the Socket e, to the Middle of the End E of the Ruler DE may be equal to the Middle of the End E from the Point B: and the Length of the Ruler GC is such, that when the Point C is drawn out as far as possible, so that the Point L near the Middle of it falls upon the Middle of the Side DF; the Part CL is equal to the Part EB, and the three Points C, D, B, are in the same streight Line, which they must always be, when the Instrument is fit for use. Upon each of the opposite Sides AE, FD, are three Scales of Divisions into 100 Parts, beginning at the Width of the Socket’s Distance from the farther Edge of the Side DE, and ending at the same Distance on the hither Side of the opposite Side FA; the outermost Scale of Divisions is of 100 equal Parts, the middlemost is made by extracting the Square Root of each of the Numbers between 1 and 100, and multiplying that Root by 10, as to find against what division of the equal Parts 25 must stand on the middle Scale. It’s Square Root 5 multiplied by 10, is 50; wherefore 25 must stand against 50 on the equal Parts, and so of others. Just after the same manner is the inner Scale made, viz. by extracting the Cube Root of each Number between 1 and 100, and multiplying the Root by 100. The same Scales of Divisions are likewise upon the part, or half CL, of the long Rule GC, beginning near the Point C. The first of these Divisions of equal Parts are for fixing the long Rule CG, and the Sockets, so as to readily describe a Figure, whose Circuit shall have a given Proportion to the Circuit of a given similar Figure. The second, for the Description of a Figure whose Area shall have a given Proportion, to the Area of a given similar Figure. And the third, for the Description of the representation of a Solid that shall have a given Proportion to a given Solid.

Dd is a turned Brass Pillar about \(\frac{3}{4}\) of an Inch long, with a Worm at the End to go into a very even Table; the Sides FD, DE of the Parallelogram are fastened to the Top D of this, so as to be any ways moveable horizontally. And at the Ends B, C, are equal round Holes wherein are put a Steel Point Cc for moving over every part of a given Figure or Draught, and a Pencil Point Bb for describing a Figure or Draught similar to a given one. Lastly, The turned Brass Pillar Aa has a free horizontal Motion about the Point A, and a little Wheel a upon the Bottom of it to run upon the Table, like one of the Legs of a Child’s Go-Cart. The Lengths of these Pillars and the two Points Cc, Bb must be such, that in all Positions of the Parallelogram the Points d, c, b, a, may be in one Plane, viz. upon the Surface of the Table, or of a Paper laid upon it.

The Use of this Instrument is contained in the Description, sufficiently to be apprehended by any intelligent Person.

II. Of the Camera Obscura.

This is a Room darkened in the Day-time, and chiefly when the Sun shines, having a Convex-Glass or Lens placed in an Hole in the Window-shutter, through which Glass the Light only passes into the Room; which Glass if properly placed, will project the Pictures of Objects from without Doors, inverted upon any white upright Surface within the Room, placed at it’s focal Distance from the Glass. And here it is to be noted, first, that the Pictures will appear more bright and lively in the Morning, if the Window and Objects be to the West, and contrariwise in the Afternoon, if the Window and Objects be to the East, and about Noon if the Window and Objects be Northwardly.

For the Convenience of directing the Axis of the Glass towards any Object, the Lens is placed in a large cylindrical Hole boared through the middle of a wooden Ball, called a Sky Optick-ball, which is easily moved about it’s Centre, within a hollow wooden Zone, and fastened to the Window-shutter: This Zone consists of two half Zones screwed together in the middle after the Ball was let in; and the Concavity of the Zone hinders the Light from passing between it and the Ball.

When the focal Distance of the Lens is 8 or 10 Feet, the Pictures of the Objects may be received upon a large Screen covered with white Paper, or Linnen, or painted white, and to have it moveable upon small Wheels, that so it may be brought to a proper Distance from the Lens.

The Pictures of the Objects will be so much the larger as the focal Distance of the Lens is longer, and so much the brighter, all things else the same, as it’s Aperture is larger.

The inverted Pictures may be viewed upright by reflecting them downwards upon a Table by means of a Looking-Glass, whose Surface is set at an half right Angle, or thereabouts, to the Horizon.

To draw Copies of Prints, Paintings, &c. by tracing their Pictures formed by the Lens.

Place the Original at a proper Distance without Doors, and let it’s Picture within the dark Room be received upon a Sheet of Paper, or upon a large plane Glass, not polished on one side, this Glass being placed upright with it’s rough side turned from the Window, you may easily trace upon it with a Black-lead Pencil, the Out-Lines of the Picture. And if a Sheet of fine Paper be strained over the Glass, the Strokes of the Pencil will appear through it when held against the Sky-light; and thus the Picture may be drawn upon the Paper. But note, The easiest way of making the Image distinct upon the Glass, when fixed, is to place the Lens in a Tube that shall slide within another short Tube fixed in the Window-Shutter.

To do this without the Trouble of making two Draughts.

Having strained the drawing Paper upon a smooth Board, lay it upon a firm Table, to be placed under the Lens in the Window-shutter, and let an inclined Looking-Glass ghik, to reflect the Picture upon that Paper, be fixed over the Table as thus, ab and cd (Fig. 2. N. I.) are two Boards fixed upright upon the Table on each hand of the drawing Paper pq; and ef is a third Board equal in Length to the Distance between the upright Boards having a round Pin at each End of it; when this Board is laid over the back-side of a Looking-Glass, and screwed to the Frame of it, the Pins must be lodged in two Slits at the Tops of the upright Boards; and by two Nuts that screw upon the Pins. The Glass may be stayed at a proper Inclination for throwing the Picture directly down upon the Paper below, and then it may be made distinct by moving the Tube that holds the Lens inwards or outwards.

III. Of the portable Camera Obscura.

This Instrument when carrying or not used, is like a wooden Box, and some of them are more like very large Folio Books; the reason of the whole Contrivance is this. The Rays of Light that come from the Object PQR, after passing through the Lens E, are tending to form an Image pqr, but being reflected upwards by the Looking-Glass ABC, they form an horizontal Image oxz, upon a Glass Plane, whose unpolished side lies uppermost, upon which a Copy of the Picture may be sketched out by a Black-lead Pencil; and to the Spectator facing the Object the Picture appears upright, there is only represented in this Figure a Section of the Instrument through the Axis of the Tube that holds the Lens, and through the middle of the Box and Looking-Glass within it: The Section of the Side opposite to the Tube is not here represented, it is only a Door opening side ways; the Edges of the rough Glass at the Top are placed in two Grooves upon the Sides of the Box, and being taken off, it is placed in a Drawer ef, at the Bottom of the Box; the Looking-Glass ABC may also be drawn out of the Grooves in the Sides of the Box and lodged in the same Drawer. The square wooden Tube consists of three Parts; the innermost that carries the Lens draws inwards or outwards, to make the Pictures distinct; the Parts gh, ik, being fixed together, and to the Box, with small Bolts, may be taken asunder and put into the Box; then the Lid at at the Top, and the Door at the End, being both shut and fixed, the Instrument becomes more commodious for carriage; the inside of the Lid whose Section is at (Fig. 3.) has two Wings that open at right Angles on each Side of it, and rest upon the Sides of the Box, to darken as much as possible the Image upon the rough Glass.

IV. Of another portable Camera Obscura for drawing.

Into the middle of the top of a square Box (Fig. 4.) there is put an upright Tube, or rather a piece of a square Pyramid; in the top of which there slides a short square Tube, having a broad Object-Glass fixed in a Hole at the top of it; the focal Distance of the Glass being somewhat less than it’s utmost Height above the Bottom of the Box, where the Pictures of Objects are to be formed by it: upon one edge of the Top of this Tube there turns a Lid, having a plane Looking-Glass fixed flat upon the inside of it, and thereby capable of being stayed at any inclination proper for reflecting the Rays that come from an Object directly downwards through the Object-Glass, to the drawing Paper fixed upon the Bottom of the Box, where the Picture of the Object will be distinctly painted, when the Object-Glass is set to a proper Height: the Box being quite closed and dark within, this Picture is viewed through a small Hole in the upper Edge of the Box Hoped off from the Side opposite to the Object where the Draught’s-Man stands, and puts his Hand and Pencil through a Hole made in this side; or rather in a long piece that slides in it horizontally, according as he has occasion to move his Hand. The square Box is abcdef, the fixed Tube is g, the sliding Tube is h, the Object-Glass is o, the inclined Looking-Glass is i, the Hole for the Eye is k, that for the Hand in the Slider mn is l.

There are other portable Camera Obscura’s that have been made and are described in Books, only differing from these either in bigness or some less essential Parts. There are two of them to be seen at the End of Mr s’Gravesande’s Essay on Perspective; a large one and a small one; the former being almost like a common Chair, or Sedan, with a folding Table in it, to lay the drawing Paper upon, and in which may be put a small Stool for the Draught’s-Man to sit upon. The Convex Lens and inclined Looking-Glass is a Top over the horizontal Table: where he gives some useful Cautions.

There must be used but one Convex-Glass, since when there are two or more the true Appearance of the Object is lost: the same inconvenience will also lie in the way, when a Concave Looking-Glass is used in the Construction of the Machine.
When more than two plane Looking-Glasses are used, the Rays after a triple Reflexion become so weak as to obscure the Appearances of the Objects; and when two Looking-Glasses are used they ought to be well polished.
The Looking-Glasses must not be put into the Machine, because in such a close Place the Draught’s-Man’s Breath will fully the Glasses, which cannot happen to the Convex-Glass, by reason of it’s being inclosed within a Tube. He says also, that the Faces of-Persons may be drawn in Minature, when the Picture of the Person upon the drawing Paper is not above half an Inch, but when it is bigger it is not easy to trace out the exact Resemblance, because each Point of the Face has not the same Focus.