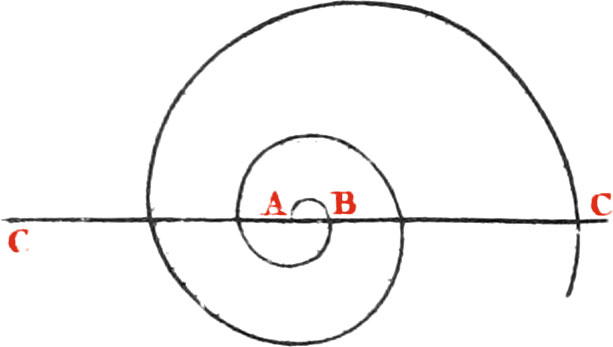
A spiral Line may be thus described If the infinite right Line AC revolves equally round it’s end A, and at the same Time a Point B moves from A equably along that right Line, and the Velocities of the Line AC, and that of the Point B along it, be as the Circumference of a Circle is to its Diameter, then will the Point B describe a spiral Line, of an infinite Number of Revolutions upon the Plane, whereon the right Line revolves. I have seen such a Spiral described upon the Surface of a round revolving Table, by drawing a Piece of Chalk, or a Pencil, held in the Hand equably along that Surface from the Centre to the Circumference. Note, There are many other Species of spiral Lines besides this here; but this is one of the most simple. Or a spiral Line may be obtained thus, by finding a great many Points through which it must pass.
The Conclusion: Containing some Miscellanies.
I. The Comparison of the English, French, Rhynland, and Roman Foot.
If the English Foot be 1; the French Foot will be 1.0654; the Rhynland Foot 1.0284; the Roman Foot 0.970, expressed in Decimal Fractions. The above Proportion of the English and French Foot is taken from the Philosophical Transactions, Numb. 465.
Mr Huygens, at page 152. of his Horolog. Oscill. says, the Paris or French Foot is to the Rhynland Foot as 144 is to 139; from whence it follows, that the English Foot is to the Rhynland Foot as 1 is to 1.0284 nearly, as is expressed above; for since the French Foot is to the English Foot, as 1.0654 is to 1; it will be as 144 is to 1.0654, so is 139 to 1.0284 nearly. The Proportion of the English Foot to the Roman Foot, viz. of 100 to 97 or 1 to .97, is taken from Dr Bernard’s Treatise of Weights and Measures. Mersennus the Jesuit says, the Roman Foot that they have in their Library at Paris, taken from the Pavement of the Capitol at Rome is 14 Lines less than their Royal French Foot; that is, the Paris Foot Royal is to the Roman Foot, as 144 is to 130. He says also, that a Roman Palm is \(\frac{1}{4}\) of a Roman Foot; and the Rhynland Foot used in many Places in Holland, which he says is thought to be equal to the antient Roman Foot, is only six Lines, or half an Inch less than their French Foot.
II. The Proportion of the English Pound Troy, and French two Mark 16 Ounce Weight, is as 16 is 21. The English Troy Ounce is to the French Ounce, as 64 is to 63. The English Avoirdupois Pound and Ounce, is to the French two Mark Weight and Ounce, as 63 is to 68 nearly. These Proportions are to be found in the aforesaid Philosophical Transaction, Numb. 465.
III. A French Wine Gallon is to an English Wine Gallon as 464.3328 is to 231, wherefore the former is very near double the latter. And a French Wine Vessel called a Muid, containing 300 French Wine Pints, or 37\(\frac{1}{2}\) French Gallons of eight Pints each, is 57.89 English Gallons of Winchester Measure. A French Pint contains 48 French cubic Inches. As 1.2092 is to 1, so is a French cubic Inch to an English cubic Inch.
IV. A short Account of the Measure of the Earth, by various Persons.
The Length of a Degree of a great Circle of the Earth, actually measured by Eratosthenes, an antient Geographer of Alexandria, about 200 Years before Christ, (which Measure was approved of, made use of, and confirmed by Ptolemy himself) is 500 Stadiums.
Some Arabian Mathematicians, at the Command of their King, about the Year 827, by Measurement, found a Degree to be 56 of their Miles, and a little more.
Alhazen, the Arabian Optician, who lived about the Year 1100, says, in his Book de Crepusculis, that the Compass of the Earth is 24000000 Paces.
Mr Snell, about the Year 1615. a famous Professor of Mathematicks at Leyden in Holland, found a Degree by Measurement to be 28500 Rhynland Perches, of 12 Rhynland Foot each. But,
Varenius, in the 4th Chapter of his General Geography, has corrected this, and makes it to be only 28300 Rhynland Perches. Varenius also gives, in that Chapter, the Manner used both by Eratosthenes and Snell, in the Measurement of their Degrees of a great Circle of the Earth. Snell’s Measure by himself is to be seen in his Treatise, entitled, Eratosthenes Batavus.
Our Countryman Mr Norwood, a Reader of Mathematicks, in a Treatise published at London, in the Year 1702. called the Sea-Man’s Practice, containing a fundamental Problem in Navigation experimentally verified, touching the Compass of the Earth and Sea, and the Quantity of a Degree in our English Measure, &c. In the Year 1635. with a Circumferentor and a Chain measuring the Distance from London to York, and taking the Difference of Latitude of those two Places, with a Sextant of more than five Feet Radius, found a Degree to be 3709 Chains, or 367196 English Feet.
Mr Picart, and other Frenchmen of the Royal Academy of Sciences, by Order of Lewis the XlVth, about the Year 1672, measured and found the Length of a Degree about Paris to be 57060 French Toises of six French Feet each. This Quadrant for finding the Differences of the Latitudes was 10 Feet Radius; and that for finding the horizontal Angles of the Triangles of Verification 3\(\frac{1}{6}\) French Feet, for he took his Lengths two Ways, by actual Measurement, and by Trigonometrical calculations of the Lengths of the Sides of several Triangles, in order for one way to prove the other. See the whole Operation (long and troublesome enough indeed, if compared to Mr Norwood’s) in Mr Picart’s Book, called, La Mesure de la Terre; or, in Dr Jurin’s Appendix to Varenius’s Geography.
Mr Cassini, in the Year 1700, by Order of Lewis the XIV, repeating the same Labour over again (likewise two Ways), carried a meridian Line of about 7\(\frac{1}{2}\) Degrees, the whole Length of France through Paris, from Dunkirk to the Pyrencan Mountains on the Borders of Spain, and makes a mean Degree to be 57292 French Toises: He used a Sextant of 10 Feet, &c. See the History of the Academy of Sciences for the 1701, as also for the Year 1718.
The Frenchmen who, in the Year 1737, measured a Degree at Tornea, under the Arctick Circle, make it to be 57437 French Toises. They used a Quadrant of 2 Feet Radius, with a Micrometer upon the Index, by means of which they have taken Angles to Seconds. (But this I am certain, the Nature of an Instrument of that short Radius will not admit.) They had also a Brass Telescope about nine Feet long, forming the Radius of a Limb or Arch of 5\(\frac{1}{2}\)°, made by the late Mr George Graham, which they used in their Business. There is a Description of this Instrument at page 124. of the. English Translation of Mr Maupertuis’s Treatise of the Figure of the Earth, determined from Observations made at the polar Circle. They measured upon a frozen River, with two Feet of Snow upon it, &c. with Rods of 30 French Foot long, and different Persons measured a Length of 7406 Toises five Feet to within four Inches, as they say. See particularly in the above Treatise of Mr Maupertuis.
Now in order to reduce all these various Measures into our English ones, thereby to compare and make them useful, we must get their reputed Proportions to ours. Mr Norwood, in his Sea-Man’s Practice, page 5, tells us, that Herodotus, Suidas, and others, make a Stadium to be 600 Alexandrian Feet. And at page 6, he says, that Here Mechanicus makes five Alexandrian Feet to be equal to six Roman Feet. But since above one Roman Foot is to an English Foot, as 972 is to 1000, therefore will one Alexandrian Foot be equal to 1.166 English Feet; but as there are 500 Stadiums in a Degree, according to Eratosthenes and Ptolemy, and as 600 Alexandrian Feet is a Stadium, there will be 300000 Alexandrian Feet in a Degree, and so according to this 300000 × 1.166 or 349800 will be the Number of English Feet in a Degree, according to Eratosthenes, being 66.25 Miles. Note, Mr Norwood, in his Book abovementioned, has mistook in saying, (page 6.) that the antient Roman Foot was greater than the English Foot; and so has Snell, and Varenius too.
Mr Norwood, in his Sea-Man’s Practice (at page 29.) says, that according to Alphraganus, the Quantity of an Arabian Mile was 4000 Cubits, or 6000 Arabian Feet; and so the Quantity of a Degree, according to the Arabian Mathematicians of 56 of their Miles, as mentioned above, will be 336000 Arabian Feet; but, says Mr Norwood, the Length of their Foot is something uncertain; they only say, it is the Length of 96 Barley-Corns laid side by side. Now this being granted, I myself found upon Trial, that 23 Barley-Corns, laid side by side, extended nearly three Inches; and so, according to this, an Arabian Foot is to our English Foot, nearly as 96 is to 92, or as 24 is to 23. Wherefore, as 23 is to 24, so is 336000 Arabian Feet, to 350608 English Feet, in a Degree, or about 66.39 English Miles. Now Mr Norwood reckons a Degree of this Measurement to be much more, viz. 370222 English Feet. But he was misled by Mr Snell, who says, that by Trial he found one Rhynland Foot to be equal to 90 Barley-Corns laid side by side, and 96 Rhynland Feet to be about 91\(\frac{1}{6}\) English Feet; whereas the true Proportion of one English Foot to one Rhynland one, is very nearly as 1 to 1.0284.
Again, Alhazen’s Account of 24000000 Paces in the whole Compass of the Earth and Sea may be nearly reduced to our English Measures thus; there must be 66666\(\frac{2}{3}\) of these Paces in one Degree. And as a Pace is by all allowed to be five Feet, there must be 333333 Arabian Feet in a Degree; but since above it appears, that an English Foot is to an Arabian Foot nearly as 23 is to 24, therefore there will be 347825 English Feet in one Degree of Alhazen’s Compass of the Earth, being about 65.87 English Miles. Mr Norwood at page 29. of his Sea-Man’s Practice, makes this Degree to be more, viz. 367283 English Feet. But herein he is also deceived by making 90 Arabian Feet equal to 99\(\frac{1}{6}\). English ones, when 90 of them should but be equal to about 93.9 English Feet.
Again, it is easy to reduce Mr Snell’s Measure of 28500 Rhynland Perches to a Degree, into English Feet, by having given the Proportion 1 to 1.0284 of an English Foot to a Rhynland one, for there will be 342000 Rhynland Feet in one Degree; and so 351712 English Feet, or taking Varenius’s Corrections of Snell’s Measure, viz. being to Snell’s in the Proportion of 235 to 283, a Degree of Mr Snell’s will be 349244 English Feet, or about 66.1 English Miles.
Again, Mr Picart’s Measure of a Degree reduced to English Feet, from the Proportion 1,0654 to 1, of a French Foot to an English one, will be 364710 English Feet, or 69.07 English Miles. Mr Cassini’s Measure of 57437 Toises, will be 367160 English Feet, or about 69.5 Miles. And, lastly, The Frenchmens Measure of 57437 Toises, to a Degree under the Arctick Circle, will be 367656 English Feet, or about 69.68 English Miles. Now all these various Measures of a Degree in English Feet, when brought together, will stand thus:
| Eng. Feet. | |
|---|---|
| Eristothenes or Ptolomy’s | 349800 |
| The Arabian Mathematicians, or Abelseda’s | 35608 |
| Alhazen’s: | 347825 |
| Snell’s corrected | 349244 |
| Mr Norwood’s | 367196 |
| Mr Picard’s | 364710 |
| Mr Cassini’s | 367160 |
| Mr Maupertius’s | 367656 |
Upon which we may observe, that Eratosthenes and Snell’s Measures of a Degree, do not differ from one another, more than 566 English Feet, or about 188 Yards, although very differently obtained, which is some sort of a Confirmation of their being both right, whatever others have said to the contrary. Likewise Abelsedas’s Measure does not differ from Eratosthenes but 308 Feet, and from Snell’s but 1444 Feet, the former being 266 Yards, and the latter about 481 Yards. Nor does Alhazen’s Measure, which is the least of all, differ about half a Mile from Abelsedas’s; therefore the first four, and most antient of these Measures of a Degree, are not so unequal, as to be a sort of Argument for their being rejected. The other four modern Measures of a Degree, by Mr Norwood and the Frenchmen, are indeed greater, but differ from one another, more or less. For Example, Mr Norwood and Picart differ 2446 English Feet. Note, in page 33, of Mr Norwood’s Sea-Man’s Practice, it is said Mr Picart’s Measure of a Degree is 365184 English Feet, as taken from the Philosophical Transactions, Numb. 112. But this is 434 English Feet too much. Mr Maupertuis’s Measure is 901 English Feet more than Picart’s.
Hence, allowing the Earth and Sea to be one Sphere, (excepting all Mountains, and Cavities not exceeding two or three Miles in heighth Or depth, and which bare no sensible Proportion to the whole Diameter,) all the abovesaid different Measures of a Degree cannot be true; nor is it easy to know which is the truest, if it be considered,
- That the Antients knew as well how to measure Distances upon the Ground, as the Moderns.
- That their Plains being so extensive, upon which they measured the Distances for this Business, viz. those of Alexandria and the Fields of Mesopotamia, made their Work easier and less liable to Error, than the Lengths measured for the same Purpose by Mr Norwood and the French, in crooked Ways, uneven Ground, or upon Ice covered with Snow. Most of these uneven Lengths being apt to be set down too great, without much Caution, Diligence, proper Correction, and trigonometrical Computation and Verification; and this trigonometrical Measure by means of Angles near upon the Horizon is subject to Uncertainty, by reason of the horizontal Refractions, (see Dr Nettleton’s Account of this already mentioned by me) it giving the opposite Bases of the Triangles too great in length.
- I am of Opinion, the Antients could take the Latitude of a Place, and draw a meridian Line by their Gnomons, as exactly as any of the Moderns can do by their Sextants and Quadrants, armed with Telescopes. I do not find Mr Norwood had any Telescope to his Sextant more than of five Feet Radius that he used. Moreover, Mr Hevelius would not use Telescopes to his Instruments, as thinking they added nothing to the Exactness of their Use. But I think he was wrong in this.
- The Abilities of most of the Measurers, viz. Ptolemy (for at least he approved of that of 500 Stadiums to a Degree.) Mr Snell, Mr Norwood, Picart, Cassini, and Maupertius, sufficiently appear by their Works.
From what I have already said, and several other Considerations, I am so divided in my Opinion, as not to be certain which of those Measures of a Degree is the truest; and if it were not for the Uncertainty of the exact Comparison of an Alexandrian Foot to our English one, I should be apt to think Ptolemy’s Measure to be as true as any of them. Also Alhazen’s Measure might in reality come out to be nearer to the rest, if we had the exact Proportion of an Arabian Foot to an English Foot; for the Comparison by Barley-Corns is a little uncertain. However, as all the eight Measures do not differ from one another more than about three Miles in a Decree. The Medium of them all seems to be the nearest the Truth, and I think ought to be used as such, ’till it be found by many and good Experiments either to be more confirmed, or to be otherwise; and this Medium is about 67.3 Miles to a Degree. There are many other Accounts of the Measure of a Degree to be seen in Authors of no moment to mention here.
V. Of the Notes which were promised at the Beginning of the Book of Mathematical Instruments, together with a few instrumental Constructions of Geometrical Problems.
An Ellipsis is a curve lined Space, made by cutting a right Cone or Cylinder through, by any Plane, making an acute Angle with the Plane of the Base of the Cone or Cylinder.
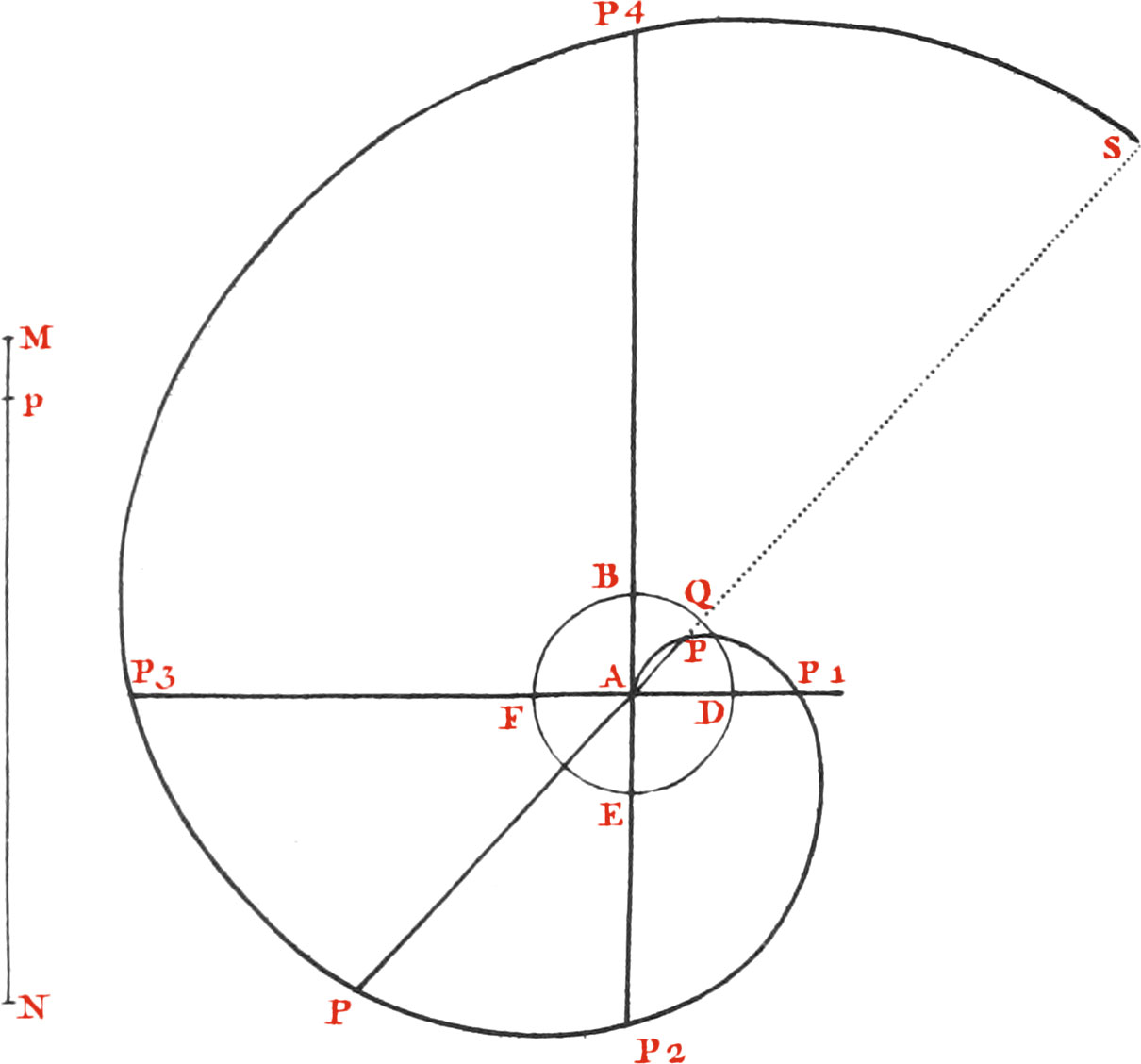
Let BDE (Fig. 26.) be a Circle, whose Centre is A, and BE, FD, two Diameters crossing one another at right Angles infinitely continued; find a right Line MN equal to the Circumference of that Circle, either by making as 7 is to 22, so is the Diameter to BE to MN or else by wrapping a String quite about the Circumference. This done, divide the right Line MN into a great even Number of equal Parts Mp, and the Circumference of the Circle FBE into the same Number of equal Parts by trial; let BQ be one of these Parts, draw the Radius AQ, and upon it take AP equal to the part Mp of the right Line MN, then will P be one Point of the Spiral, and doubling the Arch BQ, and drawing a Radius as before, upon this lay off from A, the double of the Part Mp of the Line MN, and another Point of the Spiral will be had; and by a Repetition of these Operations, with the Triples, Quadruples, &c. of the equal Arches BQ, and the equal Parts Mp. other Points will be obtained, through which the Spiral must pass. AD continued to P1, so that AP1 be equal to \(\frac{1}{4}\) MN, or \(\frac{1}{4}\) the Circumference: AE to P2, so that AP2 be equal to \(\frac{1}{4}\) MN; AF to P3, so that AP3 be equal to \(\frac{3}{4}\) MN; AB so P4, so that AP4 be equal to MN, then will P1, P2, P3, P4, be other Points of the Spiral. If AP be continued downwards, so that Ap be equal to AP2 + AP, then will p be another Point. When Points enough sufficiently near be found, and properly joined, one Revolution AP4 of the Spiral will be had; and another Revolution will be obtained, by finding Points through which it must pass thus. Continue out AP to S, so that AS be = MN + AP, then will S be one Point of this second Revolution of the Spiral. And thus may any Number of Points be found for this second Revolution. For a third Revolution AS must be = 2MN + AP, and so on, then will S be a Point of a third Revolution.
Hence the Nature of this Spiral is such, that any Radius AP is equal to the correspondent circular Arch BQ, when the Spiral has but one Revolution, when it has two, any Radius of it is equal to once the Circumference of the Circle BDEF, together with the correspondent Arch BQ of the Circle; when three, equal to twice the Circumference, added to the correspondent circular Arch BQ, and so on.
Note, This Spiral may also be described by a continued Motion, by means of a String in length equal to one or more Times the Circumference of the Circle BDEF, having a further additional Length equal to the Radius AB of that Circle; for if one end Q of such a String be fastened to the end Q, of a moveable Radius AQ, and that String be wrapped about the Circumference of the Circle, when AB and AQ coincide, and the other end A of that String be extended tightly down the fixed Radius AB, from B to A, (and there bent upwards) and that Radius A Quarrying the end Q of the String moves round from B to Q, &c. at the same Time that the other end A of the String is perpetually drawn tightly up from A to P along that moveable Radius AQ now in the Situation AQ. By this Motion the Point P, or end of the String, will describe the Spiral, for the part AP of the String is always equal to the Arch BQ, which is disengaged from as much of the String as is equal to it in length.
The Use of this Spiral is considerable in the Solutions of some difficult Problems relating to the Division of the Arches of Circles into any Number of equal Parts, or given Ratio’s, finding the sides of all regular Polygons. Dividing a Circle into two Segments that shall have a given Ratio, proving that the absolute Quadrature of the Circle is impossible, &c.
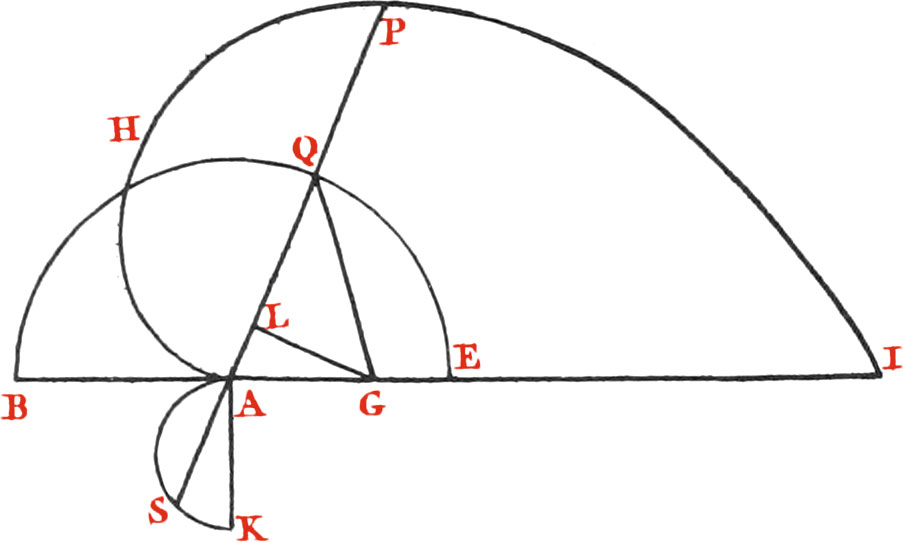
An Example of one Use is as follows: To draw aright Line GQ (Fig. 27.) from a given Point G, in the Diameter HE, of a given Semicircle BQE such, that it shall divide the same into two Segments BQG, GQE, having the given Ratio of M to N.
Let AHPI be a part of a Spiral, as above such, that any Radius AP of it be equal to the correspondent Arch BQ of the Semicircle BQE, then will AE continued out to cut the Spiral in I, be equal to the Length of the Arch BQE of the Semicircle. Make as M + N : M :: AI : R. From the Centre A of the Semicircle, raise the Perpendicular AK − AG, and upon AK describe a Semicircle, take a right Line or Ruler in length equal to R, and always making it pass through the Centre A, move one end S of it along the Semicircle KS, ’till the other end P of it cuts the Spiral in P, and the Semicircle BQE in Q, join GQ, and the Business will be done; for then will the Semicircular Space BQG be to EQG, in the given Ratio of M to N. The Demonstration is easy, for AS is always equal to the Perpendicular GL, drawn from G upon AQ, and the Space BQG is always as the Arch BQ + GL; that is, as AP + AS = R, &c.
Note, This Problem is otherwise constructed in Sir Isaac Newton’s Principia Mathem. Lib. I. by means of an Epicycloid, which he tells you there how to describe.
To trisect a given Angle ACB About the angular Point C, with any Semidiameter FC or CG, describe a Semicircle FEG, cutting the side CA of the given Angle in E; continue out GF, and laying the Edge of a Ruler NE to the Point E, so turn it that the Part NM be equal to the Radius of the Circle, then will the Arch FM be \(\frac{1}{3}\) of the given Arch EG, or the Angle FCM = ACB.
To find two continual mean Proportionals between two given right Lines X and Y. Make the rightangled Parallelogram ABCD, having its sides AB, AC, equal to the given right Lines X and Y, and describe a Circle about this Parallelogram, whose sides AC, AB, let be continued out, and laying the Edge of a Ruler EF to the Point D, turn the Ruler about ’till it’s Edge so cuts the Circle in G, and the Continuations of AC, AB in EF, that the Parts ED, GF of that Edge be equal between themselves, then will the four right Lines X, CE, BF, Y be continual Proportionals. Both these Problems are solid ones, as they are called, and cannot be constructed geometrically by the Intersection of right Lines and Circles. There are many other Ways of constructing them by the conic Sections, well known to Geometricians; but none easier in the Practice than these two above given, being in effect by the Intersection of a Circle, and the Conchoid of Nicomedes, a famous curve Line, esteemed both by Archimedes and Sir Isaac Newton, as the best for the Conduction of solid Problems, with regard to the shortness and facility of the Practice, the Curve itself being almost as easily described as the Circle; and of such a Nature, that the part of a right Line drawn from any part of the Curve to the fixed Pole intercepted by a given right Line, viz. it’s Asymptote, is of a given Magnitude.
A Parabola is a curve-lined plane Space, or Section, made by cutting a Cone by any plain Parallel, to any Plane touching the side of a Cone in a right Line. An Hyperbola is a Section or curve-lined plain Space, made by cutting a Cone, by a Plane not parallel to a Plane touching the side of that Cone in a right Line, nor passing through the Vertex of the Cone. Note, It is common to call the curve-lined Terminations of the Ellipsis, Parabola, and Hyperbola, by these Names, instead of these Planes of Section, which they really are. A Parabola opens wider and wider infinitely, according as the Cone whereof it is the Section is more continued out, and so does an Hyperbola too. Although such a Section of one Cone only, as has been described above, is usually called an Hyperbola, yet it is but one part of an Hyperbola, strictly speaking, for there is another such similar Section made by cutting the opposite Cone by the same Plane, that goes to make up one compleat Hyperbola. That is, an Hyperbola consists of two opposite similar Parts, having their Convexities next to one another, and at some Distance from each other. The middle Point of which Distance is the Centre through which those two right Lines drawn to touch the Hyperbola at an infinite Distance are called Asymptotes, and that Hyperbola whose Asymptotes are at right Angles to one another, is called an Equilateral Hyperbola, which of all the different Species is the most simple and useful.
The Ellipsis, Parabola, and Hyperbola, are called Conic Sections. If two parallel right Lines terminating in a Conic Section be bisected, and a right Line be drawn through the Points of Bisection meeting the Curve, either in one or two Points, this bisecting right Line is called a Diameter, which will bisect all Parallels to those first mentioned ones. These Parallels are called Ordinates to that Diameter, and in the Ellipsis and Hyperbola, the middle Point of any Diameter is called the Centre, and that Diameter drawn through the Centre parallel to an Ordinate to any Diameter, is called a conjugate Diameter. That Diameter whose Ordinates are at right Angles to it, is called an Axis, and the Point wherein it meets the Curve, is called the Vertex. In the Parabola each Diameter meets the Curve in one Point only, and they are all parallel to the Axis. If any two parallel right Lines terminating in a conic Section be cut by another right Line terminating in that Section, the Ratio of the two Rectangles under the Segments of those two Parallels, will be equal to the Ratio of the two Rectangles under the two Segments of the cutting Line and one Parallel, and the Segments of that cutting Line and the other Parallel. And so if this cutting Line be a Diameter, passing through the Centre, the Rectangle under the two Parts of it, cut by any Ordinate, will be to the Square of that Ordinate in a constant Patio, viz. as the Square of that Diameter is to the Square of the conjugate Diameter, or as that Diameter is to a third Proportional to those two conjugate Diameters which third Proportional is called the Latus rectum of those Diameters. But in the Parabola, the Square of any Ordinate is equal to the Rectangle under the Segment of the Diameter intercepted between the Vertex and that Ordinate, and a right Line of a constant Magnitude, called the Latus rectum, or Parameter of that Diameter. Moreover, in the Hyperbola and Ellipsis, the Tangent at the Extremity of any Semi-ordinate to a Diameter, and that Semi-ordinate will so cut that Diameter, as that the Rectangle under the Distances of the two Points of Section from the Centre, will be always equal to the Square of half that Diameter. And in the Parabola any Tangent cuts a Diameter continued out, as far beyond the Vertex of that Diameter, as the Semi-ordinate of that Diameter, drawn from the Point of Contact is distant from the said Vertex. In the Hyperbola two infinite Tangents, viz. the Asymptotes cross one another in the Centre; and if it be made as the Semi-axis is to the Distance from the Centre of any Semi-ordinate, so is that Semi-ordinate to a fourth Proportional, and a Perpendicular raised at one Vertex of the Axis be made equal to that fourth Proportional; a right Line drawn through the Centre and the Extremity of that Perpendicular will be one Asymptote, and the other Asymptote will be had by drawing a right Line through the Centre, making the same Angle with the Axis as the first Asymptote does. The Foci of an Ellipsis are two fixed Points in the great Axis equally distant from the Centre, by the Length of a mean Proportional between the Sum and Difference of \(\frac{1}{2}\), the great and \(\frac{1}{2}\) the letter Axis. And two right Lines drawn from those two Foci to any Point of the Curve will be equal to the greater Axis. But in the Hyperbola, the Foci are two Points in the transverse Axis equally distant from the Centre, such that the Difference of two right Lines drawn from them to any Point of the Curve will be equal to the traverse Axis. In the Parabola, the Focus is a Point in the Axis distant from the Vertex by \(\frac{1}{4}\) of the Latus rectum. In the Ellipsis and Hyperbola, two right Lines drawn from the Foci to any Point of the Curve, make equal Angles with a Tangent driven through that Point. In the Parabola, a Line drawn from the Focus to the Point of Contact of a Tangent, will make the same Angle with that Tangent as a Diameter drawn through that Point of Contact does. In the Hyperbola, if any right Line be drawn cutting the Asymptotes, as well as the Curve in two Points, the two Parts of this Line intercepted, between the Curve and one Asymptote, and the Curve and the other Asymptote, will be equal to one another. So that if this Line cuts the Curve in two Points infinitely near to one another, viz. is a Tangent to the Curve; the two Parts of that Tangent between the Point of Contact, and the Asymptotes will be equal to one another. And all Triangles made by such a Tangent, and the two Segments (from the Centre) of the Asymptotes cut off by that Tangent, will be equal to one another. Wherefore every Triangle made by a Semi-diameter drawn to the Point of Contact, by half of that Tangent, and by the Segment of one Asymptote cut off by that half of the Tangent, will be of a constant Magnitude. And if from any Point of an Hyperbola a right Line be drawn upon one Asymptote parallel to the other Asymptote, the Parallelogram under that right Line, and the Segment (from the Centre) of the Asymptote cut by it, will be of a constant Magnitude.
I have collected together these few Definitions, and fundamental Properties of the Conic Sections, for the Use of those who may have some Occasion for them, either in the Constructions of Problems, or for other Purposes, and have not the Books at hand, which treat of them fully, and as they should be; nor even know, perhaps, that the Conic Sections have such Properties.
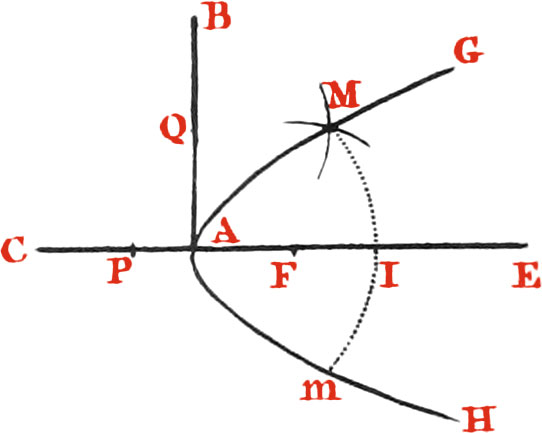
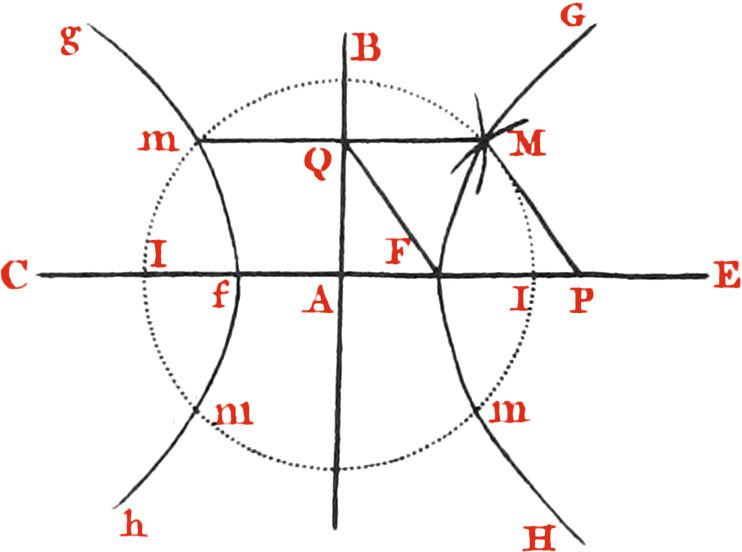
The easiest Way of describing by one Operation a Parabola and Equilateral Hyperbola by means of Points, is thus, Upon the infinite right Line CE (Fig. 30. Numb. 1, 2.) assume two Points A and F, and through A draw the right Line AB perpendicular to CE. In CE from A take any Point P on the contrary side of A that F is, for the Parabola, but on the same side for the Equilateral Hyperbola; and in this last Case greater, at such a Distance from A, that FP be greater than AF, and from P (Numb. 1.) take the Point Q in AB distant from P by the Length FP; but in (Numb. 2.) distant from F by the Length FP. This done, about the Points QF (Numb. 1.) and QP (Numb. 2.) with the Distance FP describe two Arches intersecting one another at M, and M will be one Point of a Parabola GAH, or equilateral hyperbola GFH. The former passing through the Point A, and the latter through the Point F. About the Centre A with the Distance AM describe a Circle cutting the right Line CE, or Axis of the Parabola or Hyperbola in the Points II, and make one Arch Im (Numb, i.) and three Arches Im (Numb. 2.) equal to the Arch IM, then will m be another Point of the Parabola, and m, m, m, three other Points of the opposite Hyperbola’s GFH, gfh. and by a Repetition of many more such Operations, a Number of Points M, m, may be found so near each other, as that being properly joined, a Parabola, or equilateral Hyperbola sufficiently exact, will be formed.
A Parabola, Hyperbola, and Ellipsis, may be described by a continued Motion. All three by the same way of Operation varied, by means of a moveable Square and moveable Ruler. For if the Angle of a Square be fastened to a given Point, so that the Square be moveable about the same, and the Intersection of one side of that Square and a Ruler moving parallel to itself, be carried along a given right Line; the Intersection of the other side of that Square, with that Ruler, will describe part of the Curve of the Parabola. But if the moveable Ruler, instead of moving parallel to itself, moves about a given fixed Point, and the fixed right Line be between this Point and the angular Point of the moveable Square, such an Intersection of one side of that Square, and this moveable Ruler, will describe part of the Curve of an Hyperbola. If the two fixed Points aforesaid be both on the same side, the fixed right Line, part of the Curve of the Ellipsis will be described by such a Motion. This Manner of describing the Curves of the Conic Sections is well known to Geometricians.
The following Way of describing any Hyperbola, by a continued Motion (being that of Mr De Witt’s in his Elementa Linearum Curvarum) by having the Asymptotes AE, AF (Fig. 31.) given, as also a Point B, through which the Curve is to pass is thus; from B draw BG parallel to AE cutting AF in G, take a Bevel DCF, whose Angle C is equal to the given Angle A. In the side CQ of the Bevel take the Point Q at the same Distance from C, as G is from A, and at Q fasten the end Q of a Ruler QB always passing through the fixed Point B. This done, move the side CF of the Bevel along the Asymptote AF, and the Intersection P of the Ruler QB, and the other side CD of the Bevel, will describe the part IBK of an Hyperbola passing through the Point B; and whose Asymptotes are AE, AF.
Prob. I. The Point B being given, as also the Angle EAF, and the Space S, to draw a right Line BQ, to form the Triangle APQ equal to the given Space S. (Fig. 32.) This is a noted plain Problem, but I take the easiest Way of constructing it to be by a parallel Ruler, thus: Make some Triangle ACD equal to S, then take a parallel Ruler, and letting it’s two opposite Sides PC, DQ, always pass through the given Points D, C, so move it, that a Ruler laid from B shall intersect those it’s two opposite sides at P and Q where these sides cut the sides AE, AF of the given Angle, then will the Triangle APQ be equal to the Space S.
Note, The Hyperbola within it’s Asymptotes is the only curve Line that is natural to the Construction of the Problem above, and a small Knowledge in the Nature of this Curve, is alone sufficient for any one of himself, to find out several different Constructions of the Problem, as well Mechanical as Geometrical, without any other Assistance, the Problem being in effect only to draw a Tangent to a given Hyperbola within the Asymptotes from a given Point.
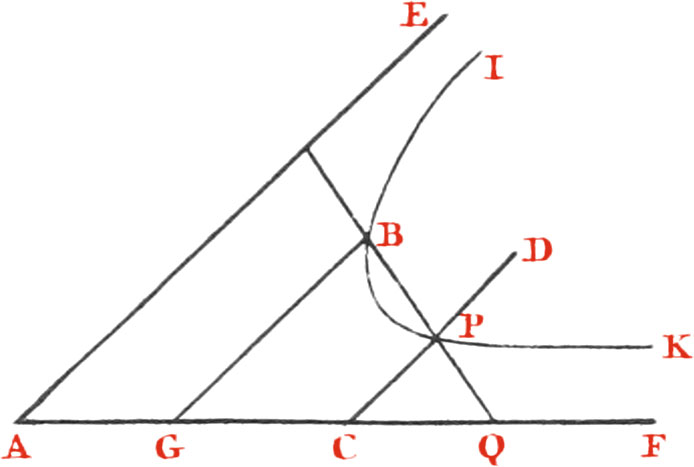
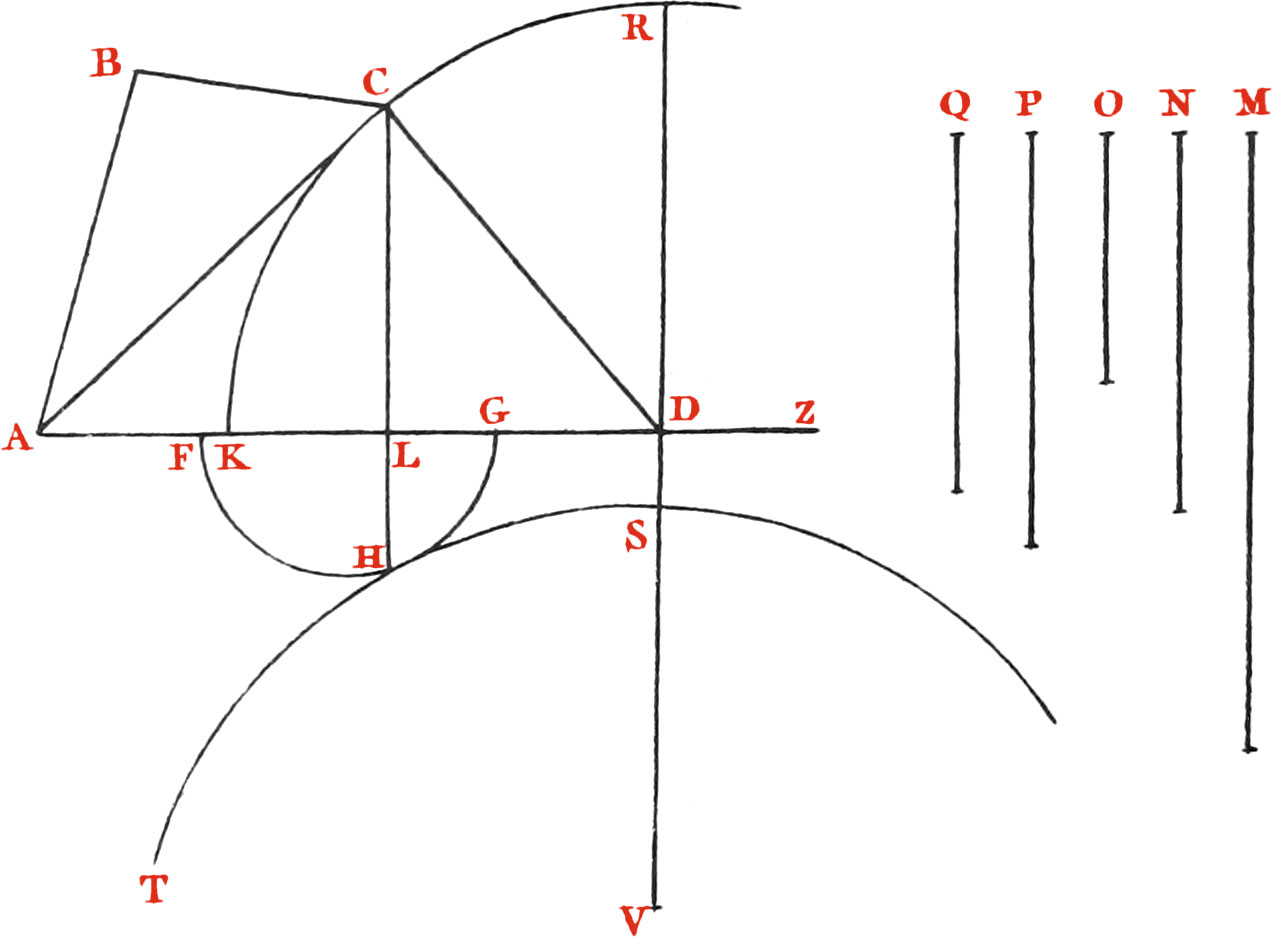
Prob. II. The Lengths of the three contiguous Chords AB, BC, CD (Fig. 33.) inscribed in a Semicircle being given: to find the Diameter of that Semicircle.
This is an old solid Problem, and it may be constructed thus: Draw two right Lines (Numb. 2.) BH, BF, at right Angles to one another, and make AB equal to one of the given Chords AB. About the Point B with a Distance BC equal to the second given Chord BC describe a Circle GCH. This done take a Square ACD, one side CD of which is equal to the third given Chord CD. Let the other side AC of this Square pass through the given Point A, while the end D of the side CD moves along the right Line BF, ’till that Square becomes so situate, that it’s angular Point C falls upon the Circumference of the Circle GCH; then will the right Line AD, joining the given Point A, and the end D of the Square thus situate, be the Diameter required of the Semicircle.
Prob. III. Given the Base AB (Fig. 34. Numb. 1.) of a Triangle ABC, the Aggregate of the sides AC, BC, and the Length of a Perpendicular BD to the side BC drawn from one of the Angles B to the other side AC, to construct the Triangle.
This is an old hypersolid Problem of Mr Ward’s, in his Compendium of Algebra, and is thus constructed. Draw (Fig. 34. Numb. 2.) two right Lines FB, BG, at right Angles to one another. Make BD equal to the given Perpendicular BD, and about the Point B with the Distance BF equal to the given Base AB describe a Circle AFH; this done, take a Thread in length equal to the given sides AC, BC taken together, and fastening one end of it to the Point B, partly extend it along the right Line BC from B to C, and partly from C through the given Point D, ’till it’s other end A falls upon the Circumference of the Circle AFH. Join the Points A and B, and the Triangle ABC required will be formed.
Prob. IV. Given the Area of a Triangle ABC, (Fig. 36.) as also it’s Perimeter, when it is inscribed in a given Circle, to construct such a Triangle.
This is an old solid Problem to be seen in Mr Ozanam’s Mathematical Dictionary, and is thus constructed. Let a Line P be equal to the given Perimeter of the Triangle, and a Line Q the side of a Square equal to the given Area; take three double Squares AEBEH, ADCDH, and CFBFH, having three equal sides EH, FH, DH, each being a third Proportional to \(\frac{1}{2}\) P and Q, and fasten their three ends H together, so as to be moveable about H like a Joint. And at any Point A of the Periphery of the given Circle, place two of the other sides AB, AC of those Squares, so as to be moveable about the said fixed Point A. This done, so move the three Squares about, as that the Intersections of the sides AB, AC, with BC always fall in the Circumference of the given Circle, at the same Time that a Thread equal to P may be extended tightly from A to B, B to C, and from C to A again. When this happens, the three sides AB, BC, AC of the three double Squares will be so situate, as to form an inscribed Triangle ABC in the given Circle, whose Circuit shall be equal to the given right Line P, and Area equal to the Square of the given right Line Q.
Note, Mr Ozanam first obtains an algebraic cubic Equation, in order to construct this Problem by the Intersection of a Parabola, and the given Circle, but such a cubic Equation may much easier be obtained after the following Manner. (See Numb. 2. Fig. 36.) Let the unknown side AC of the Triangle required be called 2x, and AC be bisected in G. Let GD be called z, and suppose DEF to be a Circle inscribed in the Triangle ABC sought. Let AB + BC + AC given be = 4a, and 2ab = to the given Area of the Triangle ABC, also let d be equal to the Diameter of the given Circle wherein the Triangle ABC is to be inscribed; then, (by the Nature of the inscribed Circle GEF) will AE = AD, EB = BF, CD = CF, and so EB + BF = 4a − 4x, and FB = EB = 2a − 2x. Wherefore AC = 2x, CB = 2a − x − z, AB = 2a − x + z. Therefore by the old Rule of finding the Area of a Triangle by having the three sides, it will be \(\sqrt{\overline{2a-2x}\ \times\ \overline{x+z}\ \times\ \overline{x-z}\ \times\ 2a}=2ab\) = \(\overline{xx-zz}\ \times\ \overline{a-x}=abb\), or \(zz=\frac{ax^3-x^3-abb}{a-x}\). Again, because from the Nature of the Circle ABC, the Rectangle under AC and CB = a Rectangle under the Diameter, and the Perpendicular drawn from C upon the opposite Side AB of the Triangle ABC; we shall have \(\frac{2x\ \times\ \overline{2a-x-z}}{d}\) = that Perpendicular; and therefore the Area of the Triangle ABC, will be \(x\ \times\ 2a-x-z\ \times\ \overline{2a-x+z}=2abd\), or \(4aa-4ax+xx-zz=\frac{2abd}{x}\), and so \(zz=4aa-4ax+xx-\frac{2abd}{x}\). But before \(zz=\frac{axx-x^3-abb}{a-x}\), wherefore \(\frac{axx-x^3-abb}{a-x}=4aa-4ax+xx-\frac{2abd}{x}\). And at length \(x^3-2axx+a^2+\frac{bb}{4}+\frac{bd}{2}x=\frac{abd}{2}\).
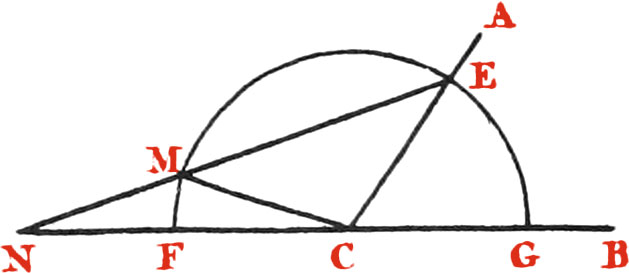
Prob. V. To constitute a Triangle FPG (Fig. 35.) such that the three sides FP, FG, PG, and the Perpendicular FH drawn from the Angle F upon the third side PG, shall be four arithmetical Progressionals.
This is the 14th Problem of Sir Isaac Newton’s universal Arithmetick, and a solid Problem. Assume any right Line FG for one of the sides of the Triangle required, and with the ends F and G of it, as Foci, with an Axis AB equal to twice that side, describe a Semi-Ellipsis ADB whose Centre is C, erect the Perpendicular GM upon the Focus G, equal to CF or CG, and upon MG describe a Semicircle MNG; this done, take a Ruler GNP always moveable about the Point G, and so turn it about, that the part NP of it beyond the Point N, where it cuts the Semicircle MNG intercepted between that Semicircle and the Ellipsis, be equal to the given focal Distance CG, or the Diameter GM of the Semicircle. Join the right Line FP, then will FPG be the Triangle to be constructed.
Upon FG describe the Semicircle FHG. Now it easily appears from the Construction, and the Nature of the Ellipsis, that FP, FG, and GP, are continual arithmetical Progressionals, for FP + PG = AB = 2FG, and from the Nature of the two Semicircles FHG, MNG t it is easily proved that the Chord GN of the Semicircle GMH is equal to one half of the Chord FH, (or perpendicular to GP) for because of the right Angles FHG, GNM, as also CGM, the right angled Triangles GNM, EFH will be equiangular. Wherefore FG : GM :: FM : GN :: 2 : 1, and so GN = \(\frac{1}{2}\)FH; and because PN = CG, it will be GP = \(\frac{1}{2}\)FH + CG; that is, 2GP = FH + 2CG, or 2GP = FH + FG; wherefore FG, GP, FH, are also arithmetical Progressionals. But FP, FG, GP, have been shewn to be such already. Wherefore now it appears, that FP, FG, GP, and FH, are four continual Progressionals.
Prob. VI. To construct a Trapezium ABCD (Fig. 37.) such, that its four sides shall be equal to four given right Lines M, N, O, P, any three of which are greater than the fourth, and whose Area shall be equal to a given Square whose side is Q.
This plain Problem is to be seen in Ozanam’s Mathematical Dictionary, where it is resolved in the worst manner possible.
Upon the indefinite right Line AZ, take AD equal to one of the given right Lines M. About the Centre D, with the Distance DC equal to the given right Line P, describe a Circle KCR. This done let N + O, be called r; N − O, s; and the Hypothenuse of a right angled Triangle, whose Base is AD and Perpendicular DC, be called h. Upon AD take DG a fourth Proportional to 2AD, the Sum of h and r, and the Difference between h and r. Also take DF a fourth Proportional to 2AD, the Sum of h and s, and the Difference of h and s. Upon FG describe a Semicircle FHG. Let KR be a Quadrant of the Circle KCR. And making CH a third Proportional to \(\frac{1}{2}\)AD and Q, from R take RS equal to CH. Continue out RS to V, so that SV be equal to RD, and about the Centre V with the Semidiameter VS describe a Circle THS, whose Centre falls at V in RD continued, cutting the aforesaid Semicircle FHG in H, from H draw HC perpenicular to AD cutting the Circle KCR in C. Join DC, and about the Centre A with a Distance equal to the right Line N describe an Arch of a Circle. Also about the Centre C, with a Distance equal to the right Line O, describe an Arch of a Circle cutting the former Arch in B. Join AB, CB, then will the Trapezium ABCD, be that required.
The Reason of the Construction will be sufficiently evident from what follows. Join AC. Let us call AD, d; AC, z; DL, x. Then, by a well known Property of a Triangle, the Area of the Triangle ABC, will be = \(\frac{1}{4}\sqrt{\overline{rr-zz}\ \times\ \overline{zz-ss}}\) = \(\frac{1}{4}\sqrt{\overline{rr-hh+2dx}\ \times\ \overline{hh-ss-2dx}}\). Since \(zz=hh-d2x\). [by 13.2 Euclid]. Let \(hh-rr=mm\), and \(hh-ss=nn\), then will the area of the Triangle ABC be \(\frac{1}{4}\sqrt{\overline{2dx-mm}\ \times\ \overline{nn-2dx}}\). Let \(mm=2dp\), and \(nn=2dq\), then will the area of the Triangle ABC be = \(\frac{d}{2}\sqrt{-xx+\overline{p+q}\ \times\ x-pq}\). Now let \(\sqrt{-xx+\overline{p+q}\ \times\ x-pq}\) be = u. And so \(xx+p\overline{p+q}\ \times\ x-pq=uu\), the Locus of which Equation will be a Circle, and by Construction DG will be equal top, since it is made as \(2d:h+r::h-r:p\). Also DF will be equal to q, since, by Construction, \(2d:h+s::h-s:q\), wherefore the Semicircle FHG will be the Locus of the Equation \(-xx+\overline{p+q}\ \times\ x-pq=uu\), any perpendicular ordinate LH being u; and therefore if ABCD be any Trapezium whose sides AB, BC, CD, AD, are equal to the given right Lines M, N, O, P, and from the Angle C of it be drawn the right Line CLH cutting the side AD in L, and the Semicircle FHG in H, the Rectangle under \(\frac{1}{4}\)AD and HL will be equal to the Triangle ABC. But the Rectangle under \(\frac{1}{2}\)AD and CL is also equal to the Triangle ACD, wherefore the Area of the Trapezium ABCD, will always be equal to the Rectangle under \(\frac{1}{2}\)AD and CL + LH; that is, equal to the Rectangle under \(\frac{1}{2}\)AD and CH. But because the Area is given, viz.
equal to \(\overline{\class{fig-label}{\mathrm{Q}^2}}\), therefore \(\overline{\class{fig-label}{\mathrm{Q}^2}}\) = \(\frac{1}{2}\)AD × CH; that is, CH is a third Proportional to \(\frac{1}{2}\)AD and Q, wherefore CH is given. Consequently the Problem will be resolved by so drawing the right Line CH of a given Length perpendicular to AD, that one of it’s Extremes C falls on the Circle KCR, and the other H on the Semicircle FHG; and this may be done by describing the Locus of the Point H, or end of a right Line CH always moving parallel to itself, while the beginning C thereof moves along the Circumference of the Circle KCR; which Locus will be the Circle THS equal to the Circle KCR, the Centre being V, and Semi-diameter VS = DR. Where this Circle interacts the Semicircle FHG, will give the Point H such, that CH being drawn will be of the given Magnitude required. The rest is sufficiently evident.
Note, I have given the instrumental Constructions of the few Problems above, as a Specimen of the most easy, natural, and obvious Way possible of performing the Business, in order to invite others to proceed in this Way in the Resolution of difficult geometrical Problems, rather than by that usual one so long in vogue, of first obtaining an algebraic Equation by means of the given Conditions of the Problem; and then finding the linear Roots of that Equation, which in almost all Cases is troublesome, unelegant, and unnatural, and in many other Cases is intolerable, and almost impossible; for Example, how difficult would it be, by the common Methods, to find the Diameter of a Semicircle, wherein 5, 7, 9, &c. given unequal and contiguous Chords may be inscribed; and how easy is it to do this by 5, 7, 9, &c. squares with the respective Number (less by two) of given Chords fastened by their Extremes to each of the Angles of those Squares, so as to be moveable about. Moreover, as every geometrical Problem points out the best and most simple Way to its own Construction, by the Intersections of some one Line (straight or curve) of a given Order, with some other Line of the same, or a different Order; those Constructions are best, when these Lines are easiest described, either by the continual Motion of Rulers, Squares, Bevels, particular Adaptions of Figures, Threads, &c. or by finding a few Points of those intersecting Lines, so many as to determine the Intersections, and when the preparatory right Lines, Perpendiculars, Parallels, Proportionals, &c. are fewest or none at all. Again, all plain Problems which have two Answers, may be constructed by the Intersections of a right Line and a Circle, or by the Intersections of two Circles, but oftentimes the Construction will be much easier and simpler done by the Intersection of a right Line and a conic Section. For Example, Vieta shews how to construct a Triangle, whose Base, Perpendicular, and Sum of the sides, are each given, by describing one Circle through two given Points to touch another Circle. But this is not the best Construction; for, if with the Extremes of the given Base, as Foci, with a Thread in length equal to the given Sum of the sides, part of an Ellipsis be described; then a Parallel to the Base at the given perpendicular Distance from it being drawn, will intersect the Curve of the Ellipsis in two Points, either of which will be the Vertex of the Triangle required; and hence it appears, that this Problem of Vieta’s is no more than drawing that Semi-Ordinate to the Axis of a given Ellipsis, which shall have a given Magnitude. And even this may be easily done without the actual Description of any Ellipsis at all differently from Vietas’s Way, upon the Consideration of the Manner of describing an Ellipsis by an elliptick Compass.
Pappus tells us, the Antients preferred Mechanical Constructions to useless Geometrical ones; and the great Dr Barrow, in his Optical Lectures, has given several most easy and natural Confirmations of difficult Problems after this way, by means of the Curve-Lines peculiar to them; and whoever delights in Constructions, will have abundance of Reason to be highly pleased with the Simplicity and Easiness of these uncommon sort of Constructions. I myself, in Imitation of Dr Barrow, have constructed many Problems after this way.
Algebra has really nothing to do in the Construction of Geometrical Problems, it’s Equations being Expressions of an Arithmetical Computation, and accordingly whatever is done by means of them is rather an Arithmetical Resolution of a Problem than a Geometrical one. Besides, when Equations of this sort arise to above two Dimensions there is no obtaining their Roots in most Cafes, unless by a troublesome Approximation; and to find the first Figures of these Roots, in order to get the other Figures, Sir Isaac Newton long ago contrived an Instrument for this purpose. A short Description of which is to be found in the Commercium Epistolicum (published by Order of the Royal Society, in the Year 1725.) at page 123, in a Letter from Mr Oldenburgh, their Secretary, to Mr Leibnitz, dated the 24th of June, in the Year 1675. He says, Sir Isaac’s Instrument consists of the Logarithms laid off upon parallel Rulers, or concentrick Circles, placed at equal Distances from one another, three Rulers being sufficient for cubic Equations, and four for biquadratick ones; they are so disposed, as that the respective Co-efficients all lie in the same right Line, from a Point of which so remote from the first Ruler, as the divided ones are from each other; a right Line is extended over them, with Directions conformable to the Nature of the Equation, by which the pure Power of a Root sought is given in one of those Rulers.