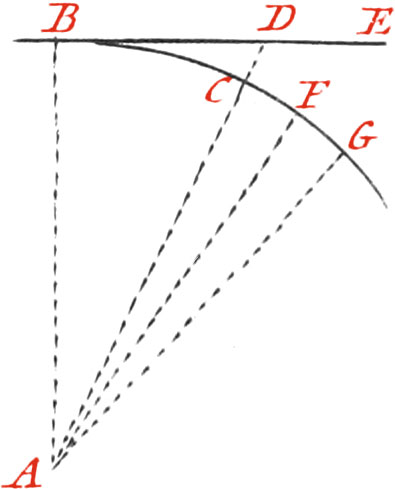
Levelling is an Operation shewing the Height of one Place in respect to another. One Place is said to be higher than another, when it is more distant from the Center of the Earth. A Line equally distant from the Center of the Earth, in all it’s Points, is called the Line of true Level; whence, because the Earth is round, that Line must be a Curve, and make a part of the Earth’s Circumference, as the Line BCFG, all the Points of which are equally distant from the Center A of the Earth: but the Line of Sight, which the Operations of Levels give, is a right Line perpendicular to the Semi-Diameter of the Earth AB, raised above the true Level, denoted by the Curvature of the Earth, in proportion as it is more extended; for which Reason, the Operations which we shall give, are but of the apparent Level, which must be corrected to have the true Level, when the Line of Sight exceeds 50 Toises.
The following Table, in which are denoted the Corrections of the Points of apparent Level, for reducing them to the true Level, was calculated by help of the Semi-Diameter of the Earth, whose Length may be known by measuring one Degree of it’s Circumference. The Gentlemen of the Academy of Sciences, have found by very exact Observations, that one Degree of the Circumference of a great Circle of the Earth, as the Meridian, contains 57292 Toises; and giving 25 Leagues to a Degree, a League will be 2291\(\frac{17}{25}\) Toises.
Now the whole Circumference of the Earth will be 9000 of the same Leagues, and it’s Diameter 2863\(\frac{7}{11}\) of them; from whence all Places on the Superficies of the Earth, will be distant from it’s Center 142\(\frac{15}{44}\) Leagues.
The Line AB represents the Semi-Diameter of the Earth, under the Feet or the Observer. The right Line BDE, represents the visual Ray, whose Points D and E are in the apparent Level of the Point B. This Line of apparent Level, serves for determining a Line of true Level, which is done by taking from the Points of the Line of apparent Level, the Height they are above the true Level in respect to a certain Point, as B; for it plainly appears from the Figure, that all the Points D, E, of the apparent Level, are farther distant from the Center of the Earth, than the Point B; and to find the Difference, you need but consider the right-angled Triangle ABD, whose two Sides AB, BD, being known, the Hypothenuse AD, may be found: from which substracting the Radius AC, the Remainder CD will shew the Height of the Point D of apparent Level, above the Point of true Level.
The Rule serving to calculate this Table, is to divide the Square of the Distance by the Diameter of the Earth, which is 6,565,179 Toises; for which Reason the Corrections are to one another, as the Squares of the Distances. Altho’ the Foundation of this Calculation be not strictly Geometrical, yet it is nigh enough the Truth for Practice.
| Distances of the Points of apparent Level | Corrections | |
|---|---|---|
| Inches | Lines | |
| 50 Toises | 0 | 0 |
| 100 Toises | 0 | 1\(\frac{1}{3}\) |
| 150 Toises | 0 | 3 |
| 200 Toises | 0 | 5\(\frac{1}{3}\) |
| 250 Toises | 0 | 8\(\frac{1}{3}\) |
| 300 Toises | 1 | 0 |
| 350 Toises | 1 | 4\(\frac{1}{3}\) |
| 400 Toises | 1 | 9\(\frac{1}{3}\) |
| 450 Toises | 2 | 3 |
| 500 Toises | 2 | 9 |
| 550 Toises | 3 | 6 |
| 600 Toises | 4 | 0 |
| 650 Toises | 4 | 8 |
| 700 Toises | 5 | 4 |
| 750 Toises | 6 | 3 |
| 800 Toises | 7 | 1 |
| 850 Toises | 7 | 11\(\frac{1}{2}\) |
| 900 Toises | 8 | 11 |
| 950 Toises | 10 | 0 |
| 1000 Toises | 11 | 0 |
If the Points of apparent Level should be taken instead of the Points of true Level, a Body would err in conducting the Water of a Source, which let be, for Example, at the Point B; for this Source will not run along the Line BDE, but will remain in the Point B; for if it should run along the Line BE, it would run higher than it is, which is impossible, because it cannot be endued with any other Figure but a Circular one, equally distant from the Center of the Earth. On the contrary, a Source in D will have a great Descent down to the Point B; but it cannot run further, because it must be elevated higher than the Source, if it continues it’s way in the same right Line, which cannot be done, unless it be forced by some Machine.