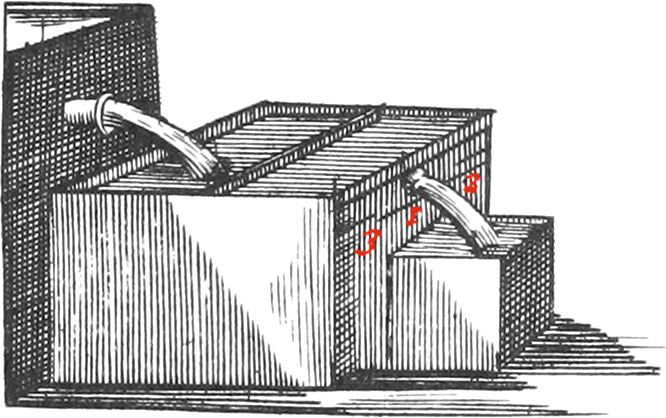
Gauge serves to know the Quantity of Water which a Source or Spring furnishes, and is commonly a Rectangular Parallelepipedon of Brass well soldered, about a Foot long, 8 Inches broad, and as many in height, more or less, according to the Quantity of Water to be measured, having several round Holes very exactly drilled in it, an Inch in Diameter, and others for Half an Inch of Water to pass thro’; and also others for a Quarter of an Inch of Water to pass thro’ them. All of which ought to be drilled so as their Centers may be at the same Height. The upper Extremes of the Inch-Holes must be within two Lines of the Top of the Gauge; and the Holes are stopped with little square Brass Plates, adjusted in the Grooves 1, 2 and 3. There is a Brass Partition, crofting the Vessel at the Place 4, fixed about an Inch from the Bottom, and drilled with several Holes, for the Water to pass more freely. This Partition is made to receive the Shock of the Water falling from the Source into the Gauge, and hindring it from making Waves, so that it may more naturally run out thro’ the Holes.
Note, The Holes which give a Cylindric Inch of Water, ought to be exactly 12 Lines in Diameter; that giving half an Inch ought to be 8\(\frac{1}{2}\) Lines, and that giving a Quarter of an Inch must be exactly 6 Lines. This may be easily found by Calculation.
To use this Instrument, it must be placed so as it’s Bottom may be parallel to the Horizon, and then let the Water of the Source run thro’ a Pipe into the Gauge (as per Figure), and when it wants about a Line of the Top, open one of the Holes (for Example) of an Inch. Then if the Water always keeps the same Height in the Gauge, it is manifest that there runs as much into it as goes out of it, and so the Source will furnish an Inch of Water. But if the Water in the Gauge riles, there must be another Hole opened, either of an Inch, half an Inch, or a Quarter of an Inch; so that the Water may keep to the same Height in the Gauge, that is, to a Line above the Holes of an Inch; and then the Number of Holes opened will give the Quantity of Water furnished by the Source.
The little Vessel receiving the Water running out of the Gauge, is to shew how much Water the Source furnishes in a determinate Space of Time: For having a Pendulum which Twines Seconds, note how many Seconds there will be in the Time that this Vessel, set under the Hole giving an Inch of Water, is filling; and exactly measuring the Quantity of Water it contains, you may have the Quantity of Water the Source furnishes in an Hour.
There has several very exact Experiments been made upon this Subject: from whence it has been found, that a Source giving one Inch of Water, will fill 14 Pints of Paris, in a Minute.
It follows from hence, that an Inch of Water gives in an Hour 8 Paris Muids, and in 24 Hours, 72 Muids.
If, for Example, a Cubic Vessel be placed under the Gauge, containing a Cubic Foot; and if the Water runs thro’ the Hole giving an Inch of Water, that Vessel will be filled in two Minutes and a half: From whence it follows, that it gives 14 Pints in a Minute, because it furnished 35 Pints in two Minutes and a half.
By this means we may know the Inches of Water a Spring or Running-Stream gives: As if, for Example, the Spring gives 7 Pints of Water in a Second; then it is said to furnish an Inch of Water: If it should give 21 Pints, then it is said to furnish 3 Inches of Water; and so of others.
To measure the Running-Water of an Aqueduct or River, which cannot be received in a Gauge, you must put a Ball of Wax upon the Water, made so heavy with some other Matter, as that there nay be but a small part of the Ball above the Surface of the Water, that so the Wind can have no power on it. And after having measured a Length of 15 or 20 Feet of the Aqueduct, you may know by a Pendulum in what time the Ball of Wax will be carried that Distance; and afterwards multiplying the Breadth of the Aqueduct or River by the Height of the Water, and that Product by the Space which the Ball of Wax has moved, this last Product will give all the Water passed, in the noted Time, thro’ the Section of the River. Example; Suppose in an Aqueduct two Feet wide, and one Foot deep, a Ball of Wax moves, in 20 Seconds, 30 Feet, which will be one Foot and a half in a Second: But because the Water moves swifter at the Top than the Bottom, you must take but 20 Feet, which will be one Foot in a Second; the Product of one Foot deep, by 2 Feet broad, is 2 Feet, which multiplied by 20, the Length, gives 40 Cubic Feet, or 40 times 35 Pints of Water, which makes 1400 Pints in 20 Seconds; and if 20 Seconds give 1400 Pints, 60 Seconds will give 4200 Pints; and dividing 4200 by 14, which is the Number of Pints an Inch of Water gives, in a Minute or 60 Seconds, the Quotient 300 will be the Number of Inches which the Water of the Aqueduct furnishes.
Mr Mariotte, who has learnedly wrote about the Motion of Water, is of opinion that Springs are nothing but Rain Water, which passing thro’ the Earth, meets with Hassock or Clay, which it cannot penetrate; and therefore is obliged to run along the Sides, and so form a Spring. For supporting this Hypothesis, he brings the following Experiment.
Having set a Cubic Vessel about a Foot high in a proper place to catch Rain-Water for several Years, he observed that the Water arose in the Vessel each Year, one with another, 18 Inches; but he thought it better to make it but 15 Inches: whence a Toise will receive in a Year 45 Cubic Feet of Water; for multiplying 36 Feet by 15 Inches, the Product will be 45 Cubic Feet.
The same Author likewise computes the Extent of Ground which supplies the River Seine with Water; and has found that the Seine is not the sixth Part as big as it might be. He has again observed, that it has but 10 Inches of Descent in 1000 Toises over-against the Invalids. He saith likewise, that, according to this supposition, the greatest Spring of Montmartre, when it is most abounding, doth not furnish over and above Water, since the Ground overwhelming it ought to send Water thereto. Whence he concludes, that there is a great deal of Water lost in the Earth.
To know the Shock Water produces, Experience has shewn that Water accelerates it’s Motion, according to the odd Numbers 1, 3, 5, 7, &c. that is, if in a fourth Part of a Second it descends one Foot in a Pipe, it will descend 3 Feet in the next fourth of a Second.
The Quantities of Water spouting out thro’ equal Holes made at the Bottoms of Reservatories, of different Heights, are to each other in the subduplicate Ratio of the Heights. The following Table shews the different Expences of Water at different Heights.
| Heights of Reservatories (Feet) | Expence of Water 3 Lines in Pipe (Pints) |
|---|---|
| 6 | 9 |
| 9 | 11 |
| 12 | 14 |
| 18 | 16 |
| 25 | 19 |
| 30 | 21 |
| 40 | 24 |
| 52 | 28 |
| Diameters of different Pipes (Lines) | Expence of Water (Pints) |
|---|---|
| 1 | 1 |
| 2 | 6 |
| 3 | 14 |
| 4 | 25 |
| 5 | 39 |
| 6 | 56 |
| 7 | 76 |
| 8 | 110 |
| Heights of Spouts (Feet) | Pints | Heights of Reservatories (Inches) |
|---|---|---|
| 6 | 5 | 1 |
| 20 | 10 | 4 |
| 20 | 21 | 4 |
| 30 | 33 | 0 |
| 40 | 45 | 4 |
| 50 | 58 | 4 |
| 60 | 72 | 0 |
| 70 | 86 | 4 |
You may see by this Table, that an Ajutage1, double another in Diameter, will expend four times the Water as that other will. Example; That of three Lines will expend in a Minute 14 Pints, and that of 6 Lines will expend 56 Pints. Note, The Ajutages must not be made Conical, but Cylindrical.