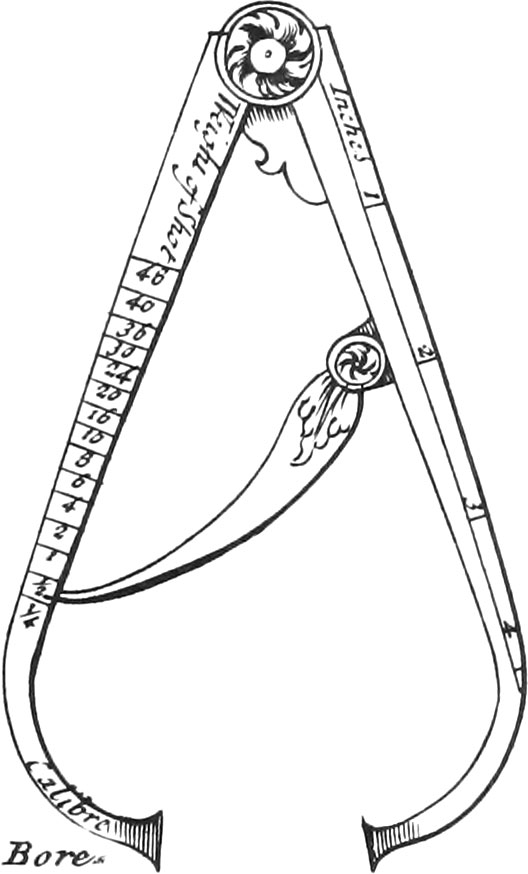
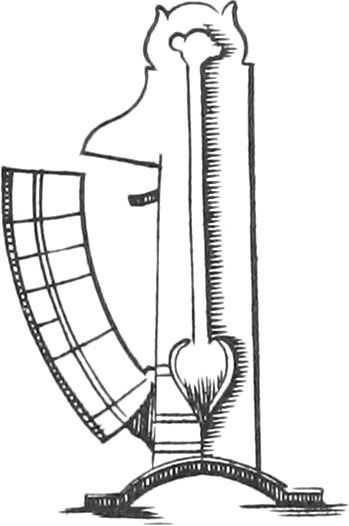
Instrument is made of two Branches of Brass, about six or 7 Inches long when shut, each Branch being four Lines broad, and three in Thickness. The Motion of the Head thereof is like that of the Head of a two-Foot Rule, and the Ends of the Branches are bent inwards, and furnished with Steel at the Extremes.
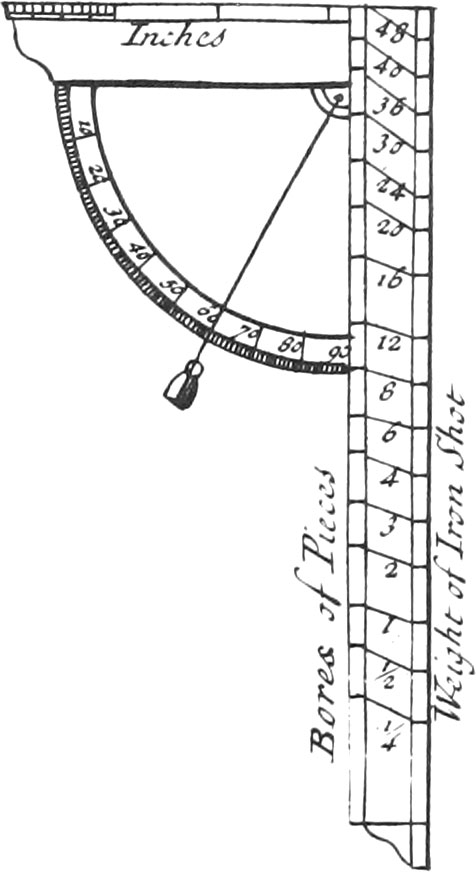
There is a Kind of Tongue fastened to one of the Branches, whose Motion is like that of the Head, for raising or lowering it, that so it’s End, which ought to be very thin, may be put into Notches made in the other Branch, on the Inside of which are marked the Diameters answerable to the Weights of Iron Bullets, in this Manner: Having gotten a Rule, on which are denoted the Divisions of the Weights, and the Bores of Pieces (the Method of dividing which will be shewn in speaking of the next Instrument), open the Callipers, so that the inward Ends may answer to the Distance of each Point of the Divisions shewing the Weights of Bullets: And then make a Notch at each Opening with a triangular File, that so the End of the Tongue entering into each of these Notches, may fix the Opening of the Branches exactly to each Number of the Weights of Bullets. We commonly make Notches for the Diameters of Bullets weighing from one fourth of a Pound to 48 Pounds, and sometimes to 64 Pounds. And then Lines must be drawn upon the Surface of this Branch against the Notches, upon which must be set the correspondent Numbers denoting the Pounds.
The Use of this Instrument is easy, for you need but apply the two Ends of the Branches to the Diameter of the Bullet to be measured; and then the Tongue being put in a convenient Notch, will shew the Weight of the Bullet.
There ought always to be a certain Proportion observed in the Breadth of the Points of this Instrument; so that making an Angle (as the Figure shews) at each Opening, the Inside may give the Weight of Bullets, and the Outside the Bores of Pieces; that is, that applying the outward Ends of those Points to the Diameter of the Mouths of Cannon, the Tongue, being placed in the proper Notch, may shew the Weights of Bullets proper for them.