Of the Construction and Uses of the English Callipers.

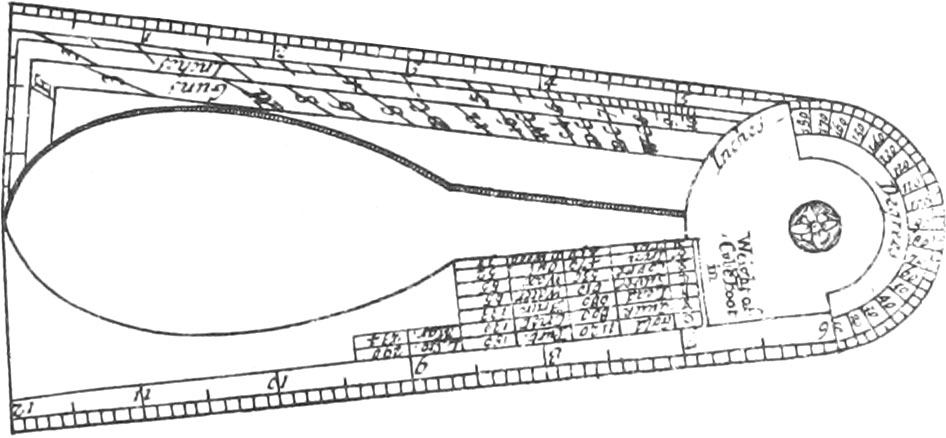
These Callipers, or Gunners Compasses, consist of two long thin Pieces of Brass, joined together by a Rivet in such a Manner, that one may move quite round the other. The Head or End of one of these Pieces is cut Circular, and the Head of the other Semi-Circular, the Center of which being the Center of the Rivet. The Length of each of those Pieces from the Center of the Rivet is six Inches; so that when the Callipers are quite opened, they are a Foot long.

One half of the Circumference of the Circular Head, is divided into every 2 Degrees, every tenth of which are numbered. And on part of the other half, beginning from the Diameter of the Semi-Circle, when the Points of the Callipers are close together, are Divisions from 1 to 10, each of which are likewise subdivided into four Parts. The Use of these Divisions and Subdivisions, is, that when you have taken the Diameter of any round thing, as a Cannon-Ball, not exceeding 10 Inches, the Diameter of the Semi-Circle will, amongst those Divisions, give the Length of that Diameter taken between the Points of the Callipers in Inches and 4th Parts.

From this Use, it is manifest how the aforesaid Divisions for Inches may be easily made: For, first, set the Points of the Callipers together, and then make a Mark for the Beginning of the Divisions; then open the Points one fourth of an Inch, and where the Diameter or the Semi-Circle cuts the Circumference, make a Mark for one fourth of an Inch. Then open the Points half an Inch, and where the Diameter of the Semi-Circle cuts the Circumference, make another Mark for half an Inch. In this Manner proceed for all the other Subdivisions and Divisions to Ten.

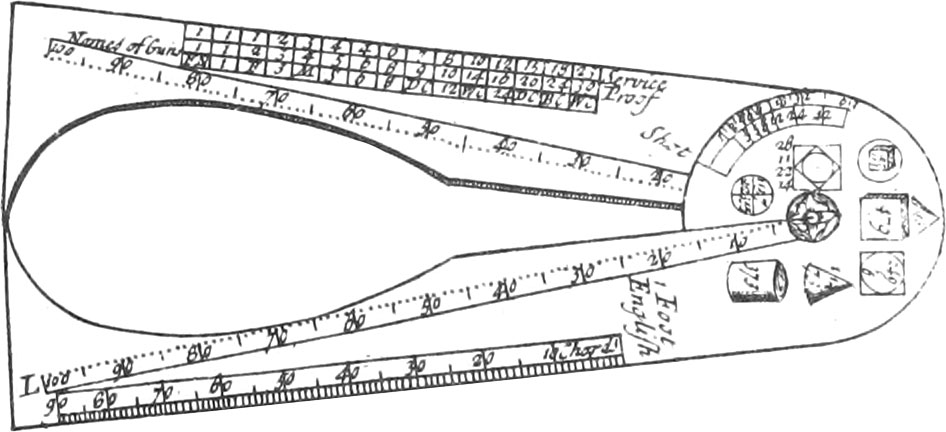
Upon one of the Branches, on the same Side the Callipers, are, First, half a Foot or six Inches, each subdivided into ten Parts: Secondly, a Scale of unequal Divisions, beginning at two, and ending at ten, each of which are subdivided into four Parts. The Construction of this Scale or Lines will be very evident, when it’s Use is shewn, which is thus: If you have a Mind to find how many Inches, under 10, the Diameter of any Concave, as the Diameter of the Bore of any Piece of Ordnance is in length, you must open the Branches of the Callipers, so that the two Points may be outwards; then taking the Diameter between the said Points see what Division, or Subdivision, the outward Edge of the Branch with the Semi-circular Head, cuts on the aforesaid Scale of Lines, and that will be the Number of Inches, or Parts, the Diameter of the Bore of the Piece is in Length. Therefore the Divisions on this Scale may be made in the same Manner as I have before directed, in shewing how to make these Divisions for finding the Diameters of round Convex Bodies.

Thirdly, The two other Scales of Lines on the same Face of the same Branch, shew when the Diameter of the Bore of a Piece of Cannon is taken with the Points of the Callipers outward, the Name of the Piece, whether Iron or Brass, that is, the Weight of the Bullets they carry, or such and such a Pounder, from 42 Pounds to 1. The Construction of these Scales are from experimental Tables in Gunnery.

On the other Branch, the same Side of the Callipers, is, First, six Inches, every of which is subdivided into 10 Parts. Secondly, A Table shewing the Weight of a Cubic Foot of Gold, Quick-silver, Lead, Silver, Copper, Iron, Tin, Purbec-Stone, Chrystal, Brimstone, Water, Wax, Oil, and dry Wood.

On the other Side of the Callipers, is a Line of Chords to about three Inches Radius, and a Line of Lines on both Branches, the same as on the Sector.

There is also a Table of the Names of the following Species of Ordnance, viz. a Falconet, a Falcon, a Three-Pounder, a Minion, a Sacker, a Six-Pounder, an Eight-Pounder, a Demi-Culverin, a Twelve-Pounder, a Whole-Culverin, a Twenty-four-Pounder, a Demi-Cannon, Bastard-Cannon, and a Whole-Cannon. Under these are the Quantities of Powder necessary for each of their Proofs, and also for their Service.

Upon the same Face is a Hand graved, and a Right Line drawn from the Finger towards the Center of the Rivet. Which Right Line shews, by cutting certain Divisions made on the Circle, the Weight of Iron-shot, when the Diameters are taken with the Points of the Callipers, if they are of the following Weights, viz. 42, 32, 24, 18, 12, 9, 6, 4, 3, 2, 1, 1\(\frac{1}{2}\), 1, Pounds. These Figures are not all set to the Divisions on the Circumference, for avoiding Confusion. The aforesaid Divisions on the Circumference may be thus made: First, When the Points of the Callipers are close, continue the Line drawn from the Finger on the Limb, to represent the Beginning of the Divisions. Now, because from Experience it is found, that an Iron Ball or Globe weighing one Pound is 1.8 of an Inch, open the Callipers, so that the Distance between the two Points may be 1.8 of an Inch; and then, where the Line drawn from the Finger cuts the Circumference, make a Mark for the Division 1. Again, to find where the Division 1.5 must be, say, As 1 is to the Cube of 1.8, So is 1.5 to the Cube of the Diameter of an Iron Ball weighing 1.5 Pounds, whose Root extracted will give 2.23 Inches. Therefore open the Points of the Callipers, so that they may be 2.23 Inches distant from each other; and then, where the Line drawn from the Finger cuts the Circumference, make a Mark for the Division 1\(\frac{1}{2}\). The Reason of this is, because the Weights of Homogeneous Bodies, are to each other as their Magnitudes; and the Magnitudes of Globes and Spheres, are to each other as the Cubes of their Diameters.

Proceed in the aforesaid Manner, in always making 1 the first Term of the Rule of Three, and the Cube of 1.8 the second, &c. and all the Divisions will be had.

Upon the Circle or Head, on the same Side of the Callipers, are graved several Geometrical Figures, with Numbers set thereto. There is a Cube whose Side is supposed to be 1 Foot, or 12 Inches, and a Pyramid of the same Base and Altitude over it: On the Side of the Cube is graved 470, signifying that a Cubic Foot of Iron weighs 470 Pounds; and on the Pyramid is graved 156\(\frac{2}{3}\), signifying that the Weight of it is so many Pounds.

The next is a Sphere, supposed to be inscribed in a Cube of the same Dimensions, as the former Cube, in which is writ 246\(\frac{1}{4}\), which is the Weight of that Sphere or Iron. The next is a Cylinder, the Diameter and Altitude of which is equal to the Side of the aforesaid Cube, and a Cone over it, of the same Base and Altitude; there is set to the Cylinder 369\(\frac{3}{14}\), signifying, that a Cylinder of Iron of that Bigness, weighs 369\(\frac{3}{14}\), and to the Cone 121\(\frac{7}{100}\), signifying, that a Cone of Iron of that Bigness weighs 121\(\frac{7}{100}\) Pounds.

The next is a Cube inscribed in a Sphere of the same Dimensions as the aforesaid Sphere. There is set to it the Number 90\(\frac{1}{4}\), signifying, that a Cube of Iron inscribed in the said Sphere, weighs 90\(\frac{1}{4}\) Pounds.

The next is a Circle inscribed in a Square, and a Square in that Circle, and again a Circle in the latter Square. There is set thereto the Numbers 28, 11, 22, and 14, signifying, that if the Area of the outward Square be 28, the Area of it's inscribed Circle is 22, and the Area of the Square inscribed in the Circle 14, and the Area of the Circle inscribed in the latter Square 11.

The next and last, is a Circle crossed with two Diameters at Right Angles, having in it the Numbers 7, 22, 113 and 355; the two former of which represent the Proportion of the Diameter of a Circle to it’s Circumference; and the two latter also the Proportion of the Diameter to the Circumference. But something nearer the Truth.