Of the Construction and Uses of the Sinecal Quadrant.

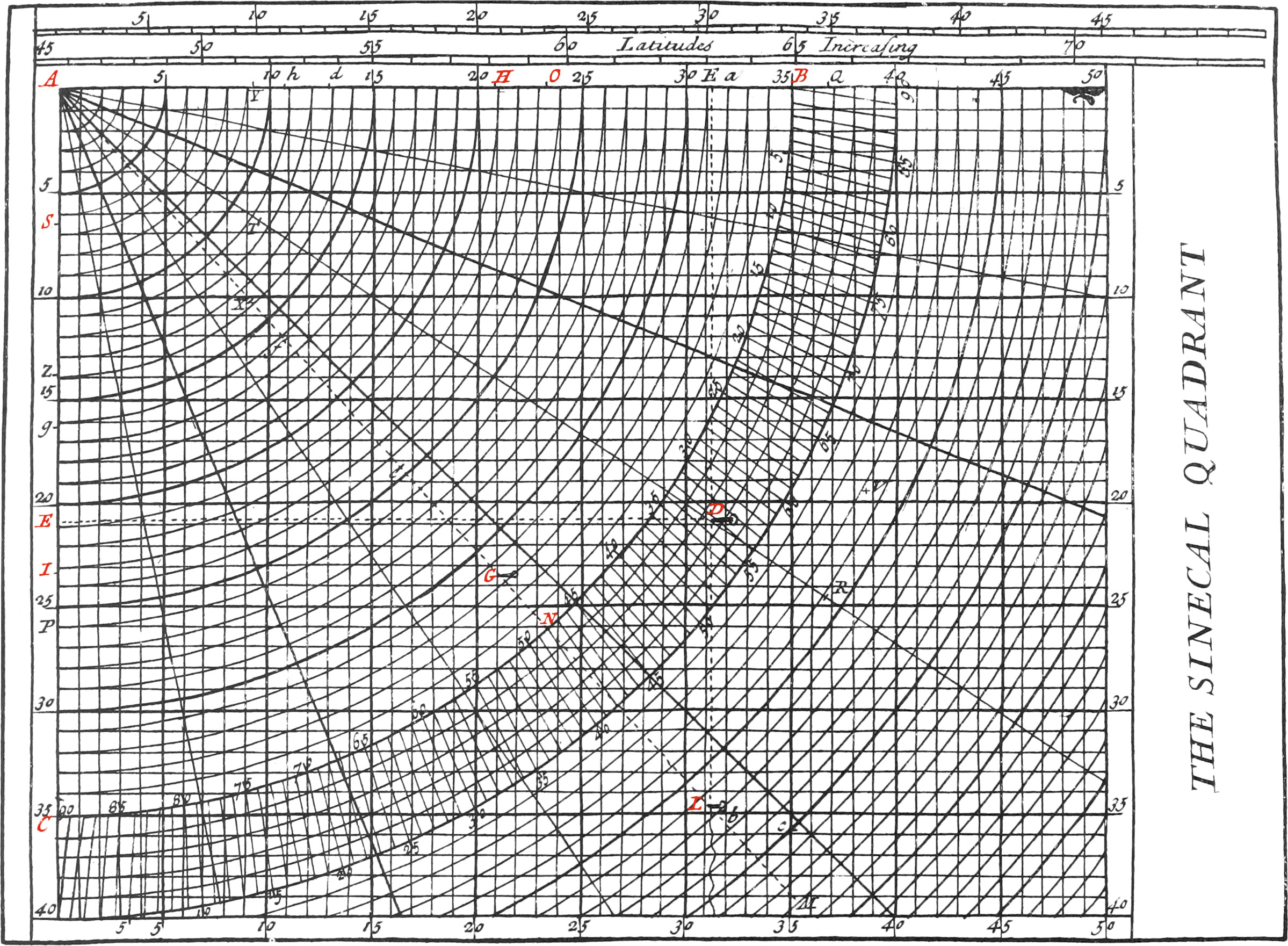
This Instrument is composed of several Quadrants, having the same Center A, and several parallel strait Lines crossing each other at Right Angles, both Quadrants and Right Lines being equally distant from each other. Now one of these Quadrants, as BC, may be taken for a quarter or fourth part of any great Circle of the Sphere, and principally for a fourth Part of the Horizon and the Meridian.

If the Quadrant BC be taken for one-fourth part of the Horizon, either of the Sides, as AB, may represent the Meridian, that is, the Line of North and South. And then the other Side AC, being at Right Angles with the Meridian, will represent the Line of East and West. All the other Lines parallel to AB are also Meridians, and all those parallel to the Side AC, are East and West Lines.

The aforesaid Quadrant is first divided into eight equal Parts by seven Radius’s drawn from the Center A, which represent the eight Points of the Compass contained in one-fourth of the Horizon, each of which is 11 Deg. 15 Min. the Arc BC is likewise divided into 90 Degrees, and each Degree divided into 12 Minutes, by means of Diagonals, drawn from Degree to Degree, and six Concentrick Circles. There is likewise a Thread, as AL, fixed to the Center A, which being put over any Degree of the Quadrant, serves to divide the Horizon as is necessary. The Construction of the rest of this Instrument, is enough manifest from the Figure thereof.

The Use of the Sinecal Quadrant.

There are formed Triangles upon this Instrument similar to those made by a Ship’s Way with the Meridians and Parallels, and the Sides of these Triangles are measured by the equal Intervals between the Concentrick Quadrants, and the Lines N and S, E and O.

These Circles and Lines are distinguished, by marking every fifth with broader Lines than the others; so that if every Interval be taken for one League, there will be five Leagues from one broad Line to the other; and if every Interval be taken for four Leagues, then there will be twenty Leagues, which make a Sea Degree, from one broad Line to the other.

Let us suppose, for example, that a Ship has failed 150 Leagues North-East, one-fourth North, which is the third Point, and makes an Angle of 33 Deg. 45 Min. with the North part of the Meridian. Now we have two things given, viz. the Course, and Distance sailed, by which a Triangle may be found on this Instrument similar to that made by the Ship’s Course, and her Latitude and Longitude; and so the other unknown Parts of the Triangle found. And this is done thus:

Let the Center A represent the Place of Departure, and count, by means of the Concentrick Arcs, along the Point that the Ship failed on, as AD, 150 Leagues from A to D; then the Point D will be the Place the Ship is arrived at, which note with a Pin. This being done, let DE be parallel to the Side AC, and then there will be formed a Right-angled Triangle AED, similar to that made by the Ship’s Course, difference of Latitude and Longitude: the Side AE of this Triangle gives 125 Leagues for the difference of Latitude Northwards, which make 6 Deg. 15 Min. reckoning 20 Leagues to a Degree, and one League for three Minutes. And lastly, the Side ED will give 83 lesser Leagues towards the East, which being reduced in the manner hereafter shewn, will give the difference of Longitude, and so the whole Triangle will be known.

Note, We call lesser Leagues those that answer to the Parallels of Latitude between the Equator and the Poles, which continually decrease the nearer they are to the Pole, and consequently also the Degrees of Longitude; and therefore the nearer a Ship sails to either of the Poles, the less way must she make to alter her difference of Longitude any determinate Number of Degrees.

Since the Center A always represents the Place of departure, it is manifest that when the Point D of arrival is found, be it in what manner soever, all the Parts of the Triangle AED will afterwards be easily determined.

If the Sinecal Quadrant be taken for a fourth part of the Meridian, one Side thereof, as AB, may be taken for the common Radius of the Meridian, and the Equator; and the other side AC, will then be half the Axis of the World. The Degrees of the Circumference BC, will represent the Degrees’ of Latitude, and the Parallels to the Side AB perpendicular to AC, assumed from every Point of Latitude to the Axis AC, will be the Radius’s of the Parallels of Latitude, as likewise the Sine-Complements of those Latitudes.

If, for Example, it be required to find how many Degrees of Longitude 83 lesser Leagues make in the Parallel of 48 Deg. you must first extend a Thread from the Center A, over the 48th Dig. of Latitude on the Circumference; and keeping it there, count the 83 Leagues proposed on the Side AB, beginning at the Center A. These will terminate at H, in allowing every small Interval four Leagues, and the Interval between the broad Lines twenty Leagues. This being done, if the Parallel HG be traced out from the Point H to the Thread, the part AG of the Thread, shews that 125 greater Leagues, or the equinoctial Leagues, makes 6 Deg. 15 Mm. in allowing 20 Leagues to a Degree, and three Minutes for one League; and therefore the 83 lesser Leagues AH, which make the difference of Longitude of the supposed Course, and which are equal to the Radius of the Parallel GI, make 6 Deg. 15 Min. of the said Parallel.

Let it be required, for a second example, to reduce 100 lesser Leagues into Degrees of Longitude on the Parallel of 60 Degrees. Having first extended the Thread from the Center A over the 60th Degree on the Circumference, count the 100 Leagues of Longitude on the Side AB, and the Parallel terminating thereon being directed to the Thread, the part of the Thread assumed from the Center, shews that 200 Leagues under the Equator make 10 Degrees; that is, 100 Leagues in the Parallel of 60 Degrees make 10 Degrees of Longitude, since every Degree of a great Circle is double to any Degree of the Parallel of 60 Degrees.

On one Side of this Instrument is put a Scale, called a Scale of Cross Latitudes, whose Construction and Division is the same as that of the Meridian Line of Mercator’s Chart, of which we shall speak by and by. The Use of this Scale is to find a mean Parallel between that of Departure and that of Arrival.

When a Ship has sailed on an oblique Course, that is, neither exactly North, South, East, or West; these Courses, besides the North and South greater Leagues, give lesser Leagues eastwardly and west hardly, which must be reduced to Degrees of Longitude. But these Leagues were made neither upon the Parallel of Departure, nor upon that of Arrival, for they were made upon all the Parallels between those of Departure and Arrival, and are all unequal between themselves, and consequently we are necessitated to find a mean proportional Parallel between that of Departure and that of Arrival, which for this reason is called a mean Parallel, and serves to reduce Leagues made in sailing a-cross divers Parallels, into Degrees and Minutes of the Equator.

Now there are several ways of finding such a mean Parallel; but I shall only speak of that here, which is done by means of the Scale of increased Latitude, without Calculation, and is thus: Let it be required, for example, to find a mean Parallel between that of 40 Deg. and that of 60 Deg.

Take, by means of a Pair of Compasses, the middle between the 40th and 60th Deg. upon this Scale, and the said middle Point will terminate against the 51st Deg. which consequently will be the mean Parallel sought.

Note, Because this Scale is in two Lines, you must take the Distance from 40 Deg. of Latitude to 45 Deg. which is on one Side, and lay it off upon some separate Right-Line. This being done, you must take the Distance from 45 Deg. to 60 Deg. which is on the other Side, and join these two Spaces together; then half of these two Lines being taken between your Compasses, you must let one Foot upon the Number 60, and the other Point will fall upon 51 Deg. which will be the mean Parallel sought. After which, it will be easy to reduce the Leagues sailed Eastwardly into Degrees of Longitude, by the Sinecal Quadrant, considered as a quarter of the Meridian, in the manner as we have laid down in the two Examples abovementioned.

This Figure represents a Mercator’s Chart. But before we give the Construction and Uses thereof, it is necessary to observe that when a Ship sails upon any determinate Point of the Compass, she always makes the same Angle with all the Meridians she passes over upon the Surface of the Terraqueous Globe.

If a Ship sails North and South, she makes an infinitely acute Angle with the Meridian she describes, that is, she runs parallel to it, or rather sails upon it.

If a Ship sails due East and West, she cuts all the Meridians at Right Angles; for she either describes the Equator, or some lesser Circle which is parallel thereto. But if her Course be on any Point between the North and East, North and West, South and East, or South and West, then she will not describe a Circle; because a Circle drawn oblique to the Meridians, will cut all of them at unequal Angles, which the Ship must not do while she sails upon any determinate Point, unless North and South, or East and West; therefore she describes a Curve, not circular, whole essential Property is to cut all the Meridians at the same Angle. And this is called a Loxodromick Curve, or only Loxodromy, and is a kind of Spiral, making an Infinity of Revolutions towards a certain Point, which is the Pole, and every Turn thereof approaches nigher and nigher thereto. A Ship’s Course then, except the two first abovenamed, is always a Loxodromick Curve, and is the Hypothenuse of a Right-angled spherical Triangle, whose two other Sides are the Ship’s Way in Longitude and Latitude. Now we have the Latitude commonly given by Observation, and the Loxodromick Angle by the Compass; therefore by Trigonometry we may find the Hypothenuse, or the Way that the Ship has failed, &c.

But because the Calculation of a Ship’s Way by means of the Loxodromick Curve is troublesome, therefore the Ancients sought after some Method whereby a Ship’s Way might be a strait Line, which might nearly preserve the Property of the Loxodromick Curve, which is, to cut all the Meridians under the same Angle. But they found this absolutely impossible upon the account of the Meridians not being parallel between themselves, as in reality they are not. And therefore they supposed the Meridians to be parallel strait Lines; and so from this supposition it follows, that the Degrees of Longitude unequally distant. from the Equator, are of the same bigness; whereas they really always diminish from the Equator, in a certain known Proportion, which is as Radius is to the Sine-Complement of the Latitude. But to retrieve this Error, they have supposed the Degrees of Latitude, which by the Nature of the Sphere are every where equal, to be augmented in the same Proportion as the Degrees of Longitude diminish. And so the Inequality which ought to be in the Degrees of Longitude of different Parallels, is thrown upon the Degrees of Latitude in the manner we are going to lay down.

Now Charts made in this manner are called Mercator’s Charts, because Mercator was the first that made them; and they are commonly esteemed the best: for by the Experience of several Ages, it is found that Seamen ought to have very simple Charts, wherein the Meridians, Parallels, and Rhumb-Lines, may be represented by strait Lines, that so they may prick down their Courses easily.