Book VII. Ch. II.

Of the Construction and Use of Instruments for taking the Altitudes of the Sun or Stars at Sea.

Of the Sea-Astrolabe.

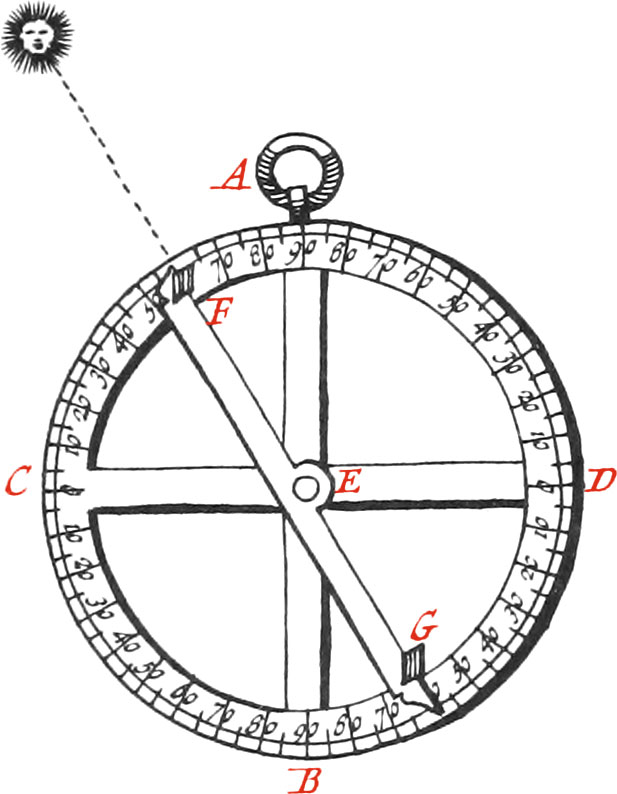
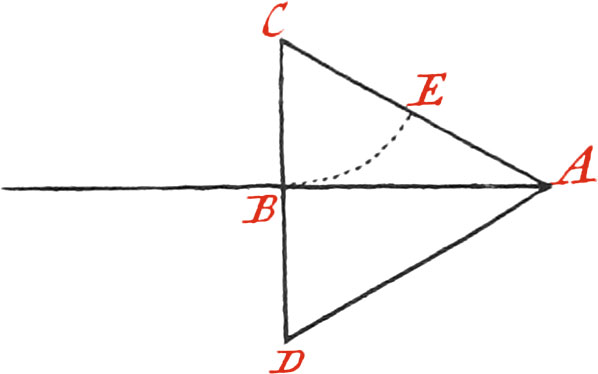
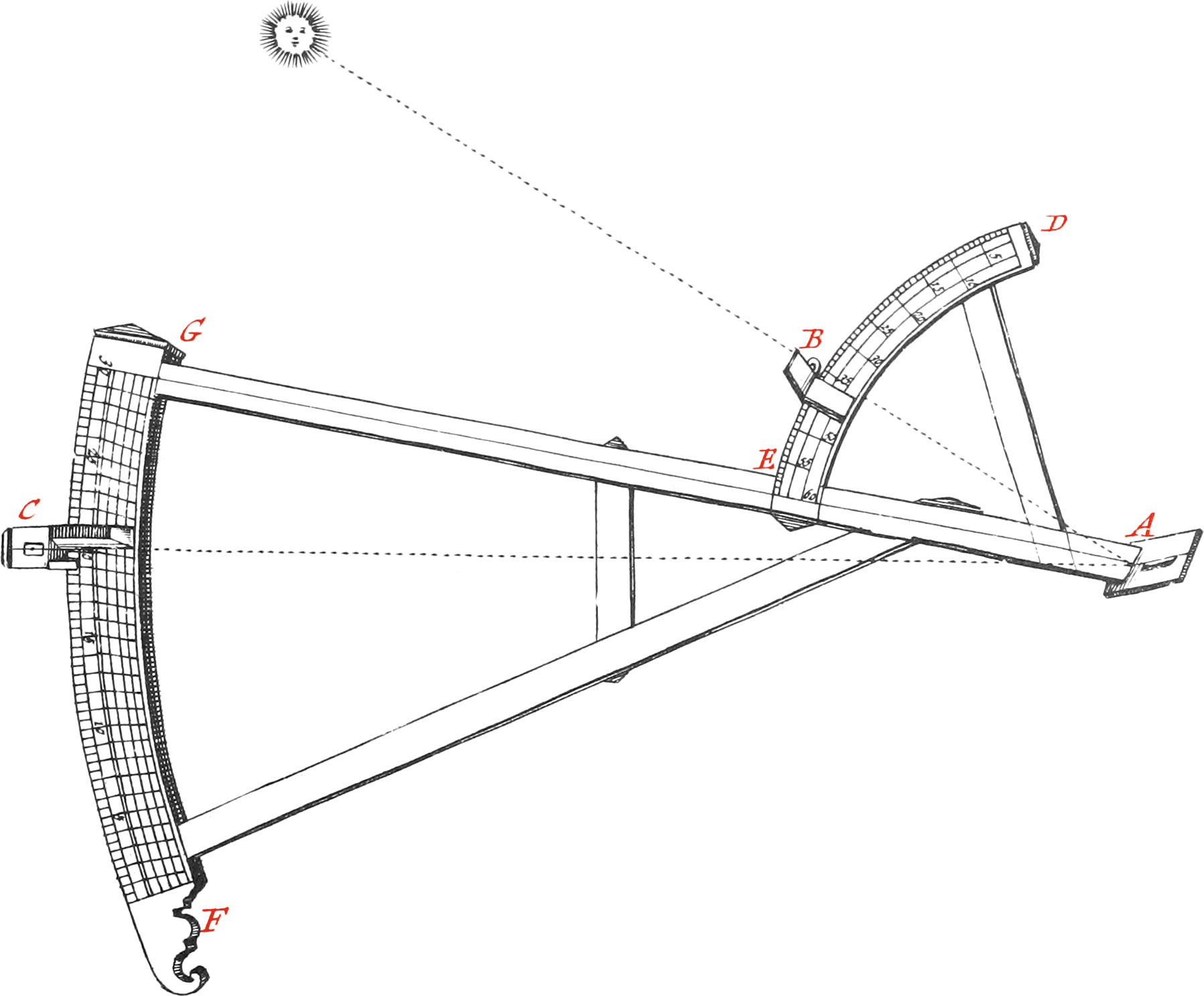
The most common Instrument for taking of Altitudes at Sea is the Astrolabe, which consists of a brass Circle, about one Foot in Diameter, and six or seven Lines in Thickness, that so it may be pretty weighty: there is sometimes likewise a Weight of six or seven Pounds hung to this Instrument at the Place B, that so when the. Astrolabe is suspended by it’s Ring A, which ought to be very moveable, the said Instrument may turn any way, and keep a perpendicular Situation during the Motion of the Ship.

The Limb of this Instrument is divided into four times 90 Degrees, and very often into halves, and fourths of Degrees.

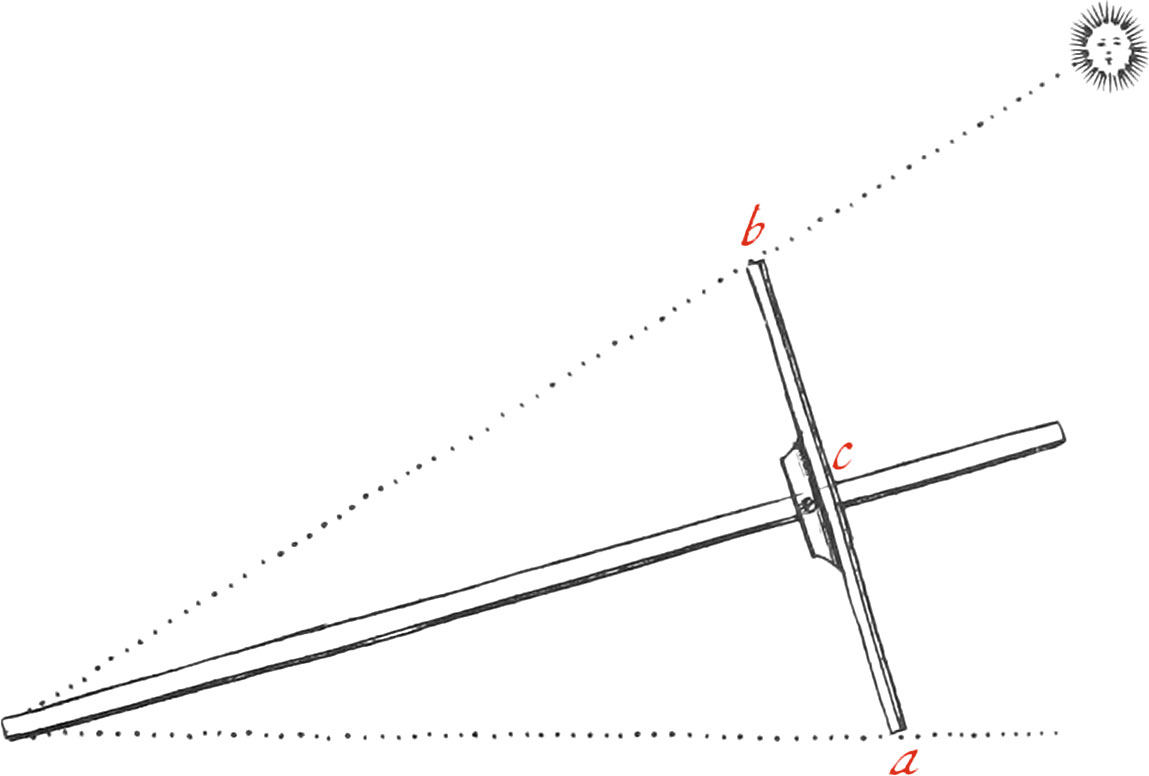
It is absolutely necessary, that the Right Line CD, which represents the Horizon, be perfectly level, that so the beginning of the Divisions of the Limb of the Instrument may be made therefrom. Now to examine whether this be so or no, you must observe some distant Object thro’ the Slits or little Holes of the Sights F and G, fastened near the Ends of the Index, freely turning about the Center E, by means of a turned-headed Rivet: I say, you must observe the said distant Objects, in placing the Eye to one of the said Sights for Example, to G: then if the Astrolabe be turned about, and the same Object appears thro’ the other Sight F, without moving the Index, it is a sign the Fiducial Line of the Index is horizontal. But if at the second time of Observation, the Index must be raised or lowered before the Object be espied thro’ the Sights, then the middle Point between the two Positions will shew the true horizontal Line passing thro’ the Center of the Instrument, which must be verified by several repeated Observations, before the Divisions of the Limb are begun to be made, in the Manner as we have elsewhere explained.

Use of the Astrolabe.

The Use of this Instrument is for observing the Sun or Stars Altitude above the Horizon, or their Zenith Distance. The Manner of effecting which, is thus: Holding the Astrolabe suspended by it’s Ring, and turning it’s Side towards the Sun, move the Index ’till the Sun’s Rays pass thro’ the Sights F and G; then the Extremes of the Index will give the Altitude of the Sun in H, upon the divided Limb, from C to F, comprehended between the horizontal Radius EC and the Rays EF of the Sun, because the Instrument in this Situation represents a Vertical Circle. Now the Divisions of the Arcs BG or AF, shew the Sun’s Zenith Distance.

The Construction of the Ring.

This Figure represents a brass Ring or Circle, about 9 Inches in Diameter, which it is necessary should be pretty thick; that so being weighty, it may keep it’s perpendicular Situation better than when it is not so heavy, having the Divisions denoted on the Concave Surface thereof. The little Hole C, made thro’ the Ring, is 45 Degrees distant from the Point of Suspension B, and is the Center of the Quadrant DE, divided into 90 Degrees, one of whose Radius’s CE, is parallel to the Vertical Diameter BH of the Ring, and the other horizontal Radius CD, is perpendicular to the said Vertical Diameter.

Now having found the said horizontal Radius CD very exactly, by suspending the Ring, &c. Radius’s must be drawn from the Center C, to each Degree of the Quadrant DE, and upon the Points wherein the said Radius’s cut the Concave Surface of the Ring, the correspondent Numbers of the Degrees of the Quadrant must be graved; and so the Concave Surface of the Ring, will be divided from F to G. This Divisioning may be first made separately upon a Plane, and afterwards transferred upon the Concave Surface of the Ring.

This Instrument is reckoned better than the Astrolabe, because the Divisions of the Degrees upon the Concave Surface are larger in proportion to it's bigness, than those on the Astrolabe.

The Use of the Ring.

When this Instrument is to be used, you must suspend it by the Swivel B, and turn it towards the Sun A; so that it’s Rays may pass thro’ the Hole C. This being done, the little Spot will fall between the horizontal Line CF, and vertical Line CG, upon the Degrees of the Sun’s Altitude on the Inside of the Ring, reckoned from F to I.

Of the Quadrant.

The Instrument of Figure 7, is a Quadrant about one Foot Radius, having it’s Limb divided into 90 Degrees, and very often each Degree into every 5th Minute by Diagonals. There are two Sights fixed upon one of the Sides AE, and the Thread to which the Plummet is fastened, is fixed in the Center A. I shall not here mention the Construction of this Instrument, because we have sufficiently spoken thereof in Chap. V. Book IV.

Now to use this Instrument, you must turn it towards the Sun D, in such manner that it’s Rays may pass thro’ the Sights A and E, and then the Thread will fall upon the Degrees of the Sun’s Altitude on the Limb, in the Point C, reckoned from B to C, and the Complement of his Altitude reckoned from E to C.

Of the Fore-Staff, or Cross-Staff.

This Instrument consists of a strait square graduated Staff AB, between two and three Foot in length, and four Crosses or Vanes FF, EE, DD, CC, which slide stiffly thereon. The first and shortest of these Vanes FF, is called the Ten-cross or Vane, and belongs to that Side of the Staff whereon the Divisions begin at about 3 Degrees from the End A, (whereat the Eye is placed in time of Observation) to 10 Degrees. Note, Sometimes the Thirty-cross EF is so made, as that the Breadth thereof serves instead of this Ten-cross.

The next longer Vane EE, is called the Thirty-cross, and belongs to that Side of the Staff, whereon the Divisions begin at 10 Degrees, and end at 30 Degrees, and this is called the Thirty-side: Half the Length of the Thirty-vane will reach on this Thirty-side, from 30 Deg. to 23 Deg. 52 Min. and the whole Length from 30 Deg. to 19 Deg. 47 Min.

The next longer Vane DD, is called the Sixty-cross, and belongs to that Side of the Staff whereon the Divisions begin at 20 Deg. and end at 60 Deg. and is called the Sixty-side. The length of this Cross will reach on this Sixty-side, from 60 Deg. to 30 Deg.

The longest Cross CC, is called the Ninety-cross, and belongs to that Side whereon the Divisions begin at 30 Degrees, and end at 90 Degrees, and is called the Ninety-side of the Staff: the Degrees on the several Sides of the Staff, are numbered with their Complements to go Degrees in small Figures.

This Staff may be graduated Geometrically thus: Upon a Table, or on a large Paper parted smoothly upon some Plane, draw the Line FG, the length of the Staff to be graduated, and on F and G raise the Perpendiculars FC and GD; upon which lay off the Length you intend for the half Length of one of the four Crosses, from F to C, and G to D, and draw the Line CD representing the Staff to be graduated. This being done, about the Center F, with the Semidiameter FG or CD, describe an eighth part of a Circle, which divide into 90 equal Parts. Then if Right Lines be drawn from the Point F, to each of the aforesaid Divisions, these Lines will divide the Line CD, as the Staff ought to be graduated.

But if this Staff is to be graduated by the Table of natural Tangents, you must first observe, that the Graduations are only the natural Co-tangents of half Arcs, the half Cross being Radius; therefore divide the length of the half Cross into 1000 equal Parts, or 100000 if possible, according to the Radius of the Tables of natural Tangents: then take from this the Co-tangents, as you find them in the Table, and prick them from F successively, and your Staff will be graduated for that Vane. So do for the rest severally. If it be required to prick down the 80th Degree, the half of 80 is 40, and the natural Co-tangent of 40 Deg. is 119175, which take from the Scale or half Cross so divided, and prick it from F to P, and that will be the Point for 80 Degrees, &c. So again, To put on the 64th Degree, half of 64 is 32, and its Co-tangent is 160033, which take from the divided Cross (prolonged), prick it from E, and you will have the 64th Degree.

Now that the Cross CD, when transferred to B, shall make the Angles CAD eighty Degrees, is demonstrable thus: Since CB the half Cross is Radius, and AB is by Construction the Tangent of 50 Deg. the Angle ACB is 50 Degrees; and since the Triangle ABC is Right Angled, the Angle BAC will be 40 Degrees: but the Angle DAC is double the Angle BAC; therefore the Angle DAC is 80 Degrees, and the Point B the true Point on the Staff for 80 Degrees. The same Demonstration holds, let the Cross be what it will.

If the Staff be to be graduated by any Diagonal Scale, measure half the Length of the Vane by the Scale, and say, As the Radius of the Tables 100000, is to the Measure of half the Cross, So is the natural Co-tangent of the half any Number of Degrees desired to be pricked on the Staff, to the Space between the Center of the Staff F, and the Point for the Degrees sought.

For Example; Suppose half the Length of the Vane, measured on a Diagonal Scale, be 945; to find what Number must be taken off the Diagonal Scale for the 80th Degree. The Co-tangent of 40 Degrees (half of 80) is 1191753, which being multiplied by 945, and divided by Radius, gives 11261. And this being taken from the Diagonal Scale, will give the Degrees desired.

The Use of the Fore-Staff.

The chief Use of this Instrument, is to take the Altitude of the Sun or Stars, or the Distance of two Stars; and the Ten, Thirty, Sixty and Ninety Crosses are to be used, according as the Altitude is greater or lesser; that is, if it be less than 10 Degrees, the Ten Cross must be used; if above 10, but less than 30 Degrees, the Thirty Cross must be used; and if the Altitude be judged to be above 30, but less than 60 Degrees, the Sixty Cross must be used. But when Altitudes are greater than 60 Degrees, this Instrument is not so convenient as others.

To observe an Altitude.

Place the flat End of the Staff to the outside of your Eye, as near the Eye as you can, and look at the upper End b of the Cross for the Center of the Sun or Star, and at the lower End a for the Horizon. But if you see the Sky instead of the Horizon, slide the Cross a little nearer to your Eye; and if you see the Sea instead of the Horizon, move the Cross a little further from your Eye, and so continue moving the Cross till you see exactly the Sun or Star’s Center by the top of the Cross b and the Horizon by the bottom thereof a. Then the Degrees and Minutes cut by the inner Edge c of the Cross, upon the Side of the Staff peculiar to the Cross you use, is the Altitude of the Sun or Star: But if it be the Meridian Altitude you are to find, you must continue your Observation as long as you find the Altitude increase, still moving the Cross nearer to your Eye; but when you perceive the Altitude is diminished, forbear any farther Observation, and do not alter your Cross; but as it stands, count the Degrees and Minutes on the Side proper to the Cross, and you will have the Meridian Altitude required, as also the Zenith Distance, by substracting the said Altitude from 90 Degrees, if it be not graduated on the Staff. To which Zenith Distance add the Minutes allowed for the Height of your Eye above the Surface of the Sea, according to the little Table in the Margin, or substract it from the Altitude, and then you will have the true Zenith Distance and Altitude.

Height of the Eye English Feet	Allowance Min.
1	1
2	1\(\frac{1}{2}\)
3	2
4	2
5	2\(\frac{1}{2}\)
6	3
7	3
8	3
9	3\(\frac{1}{2}\)
10	3\(\frac{1}{2}\)
12	4
16	4
20	5
24	5\(\frac{1}{2}\)
28	6
32	6\(\frac{1}{2}\)
36	7
40	7
44	7\(\frac{1}{2}\)
48	8

If it be hazy or somewhat thick Weather, the Fore-Staff may be used as above, but if the Sun shines out, the upper Limb of the Sun must be either observed, and afterwards his Semidiameter must be substracted from the Altitude found, or else a coloured Glass on the top of the Cross must be used, to defend the Sight from the Splendor of the Sun.

To observe the Distance or two Stars, or the Moon’s Distance from a Star, place the Staff’s flat end to the Eye, as before directed, and looking to both ends a and b of the Cross, move it nearer or farther from the Eye, ’till you can see the two Stars, the one on one end, and the other on the other end of the Cross. Then see what Degrees and Minutes are cut by the Cross on the side proper to that Vane in use; and those Degrees shew Star’s Distance.

But that there may be no Mistake in placing the Staff to the Eye, which is the greatest Difficulty in the Use of this Instrument: First, before Observation, put on the Sixty-cross, and place it to 30 Degrees on its proper Side, and also the Ninety-cross, sliding to it 30 Degrees likewise on his Right Side: this being done, place the end of the Staff to the corner of your Eye, moving it something higher or lower about the Eye, ’till you see the upper ends of the two Crosses at once exactly in a Right Line, and also their lower ends; and that is the true Place of your Staff in Time of Observation.

If the Sun’s Altitude is to be observed backwards by this Instrument, you must have an horizontal Vane to fix upon the Center or Eye-end of the Cross, as also a Shoe of Brass for a Sight Vane, to fit on to the end of any of the Crosses; then when you would observe, having put on the horizontal Vane, and fixed the Shoe to the end of a convenient Cross, turn your back to the Sun, and looking through the Sight in the brass Shoe, lift the end of the Staff up or down, ’till the Shadow made by the upper end of the Cross falls upon the slit in the Horizon-Vane, and at the same time you can see the Horizon through the Horizon-Vane. Then the Degrees and Minutes cut by the Cross on the proper Side, are the Altitude. But if there be fixed a Lens, or small double Convex-Glass, to the upper end of the Vane, to contract the Sun-beams, and cast a small bright Spot on the Horizon-Vane, this will be found more convenient than the Shadow, which is commonly imperfect and double.

Of the English Quadrant, or Back-Staff.

This Instrument is commonly made of Pear-Tree, and consists of three Vanes A, B, C, and two Arcs. The Vane at A is called the Horizon-Vane, that at B the Shade-Vane, because it gives the Shadow upon the Horizon-Vane in Time of Observation, and that at C the Sight-Vane, because in Time of Observation it is placed at the Eye. The lesser Arc DE is the Sixty Arc, and that marked FG is the Thirty Arc, both of which together make 90 Degrees, but they are of different Radius’s. The Sixty Arc DE is divided into 60 Degrees, commonly by every five, but sometimes by single Degrees. In Time of Observation, the Shadow-Vane is placed upon this Arc always to an even Degree.

The Thirty Arc GF, is divided into 30 Degrees, and each Degree into Minutes by Diagonal Lines, and Concentrick Arcs. The Manner of doing which, I have already laid down elsewhere.

The Use of the English Quadrant.

If the Sun’s Altitude be to be taken by this Instrument, you must put the Horizon-Vane upon the upper End or Center A of the Quadrant, the Shade-Vane upon the Sixty Arc DE, to some Number of Degrees less than you judge the Co-altitudes will be by 10 or 15 Degrees, and the Sight-Vane upon the Thirty Arc FG. This being done, lift up the Quadrant, with your Back towards the Sun, and look through the small Hole in the Sight-Vane C; and so raise or lower the Quadrant ’till the Shadow of the upper Edge of the Shade-Vane B falls upon the upper Edge of the slit in the Horizon-Vane A: if then at the same time the Horizon appears thro’ the said slit, the Observation is finished; but if the Sea appears instead of the Horizon, then remove the Sight Vane lower towards F; but if the Sky appears instead of the Horizon, then slide the Sight-Vane a little higher: and so continue removing the Sight-Vane, ’till the Horizon appears thro’ the slit of the Horizon-Vane, and the Shadow of the Shade-Vane falls at the same time on the said Slit of the Horizon-Vane. This being done, see how many Degrees and Minutes are cut by the Edge of the Sight-Vane C, which answers to the Sight-Hole, and to them add the Degrees that are cut by the upper Edge of the Shade-Vane, and the Sum is the Zenith Distance or Complement of the Altitude. But to find the Sun’s Meridian or greatest Altitude on any Day, you must continue the Observation as long as the Altitude be found to increase, which you will perceive, by having the Sea appear instead of the Horizon, removing the Sight-Vane lower; but when you perceive the Sky appear instead of the Horizon, the Altitude is diminished: therefore desist from farther Observation at that Time, and add the Degrees upon the Sixty Arc to the Degrees and Minutes upon the Thirty Arc, the Sum is the Zenith Distance, or Co-altitude of the Sun’s upper Limb.

And because it is the Zenith Distance or Co-altitude of the upper Limb of the Sun, that is given by the Quadrant, when observing by the upper Edge of the Shade-Vane, as it is customary to do, and not the Center; you must add 16 Min. the Sun’s Semi-diameter, to that which is produced by your Observation, and the Sum is the true Zenith Distance of the Sun’s Center. But if you observe by the lower part of the Shadow of the Shade-Vane, then the lower Limb of the Sun gives the Shadow; and therefore you must substract 16 Min. from what the Instrument gives: but considering the Height of the Observator above the Surface of the Sea, which is commonly between, 6 and 20 Feet, you may take five or six Minutes from the 16 Minutes, and make the allowance but 10 Min. or 12 Min. to be added instead of 16 Min.

Note also, The Refraction of the Sun or Stars causes them to appear higher than they are; therefore after having made your Observation, you must find the convenient Refraction, and substract it from your Altitude, or add it to the Zenith Distance, in order to have the true Altitude or Zenith Distance.

If a Lens or double Convex-Glass be fixed in the Shade-Vane, which contracts the Rays of Light, and casts them in a small bright Spot on the Slit of the Horizon-Vane instead of a Shade, this will be an Improvement to the Instrument if the Glass be well fixed; for then it may be used in hazy Weather, and that so thick an Haze, that an Observation can hardly be made with the Forestaff: also in clear Weather the Spot will be more defined than the Shadow, which at best is not terminated.

Of the Semi-circle for taking Altitudes at Sea.

This Semi-circle is about one Foot in Diameter, and the Limb thereof is divided into 90 Degrees only, each of which are quartered for 15 Min. At A and B are two Sights fixed to the Extremes of the Diameter, and another at C, so adjusted as to slide on the Limb of the Semi-circle, that so the Sun’s Rays may pass thro’ it when the Instrument is using.

The Use of the Semi-circle.

If an Altitude is to be taken forwards by this Instrument, the Eye must be placed at the Sight A, and then you must look thro’ the Sights A and B at the Horizon, and slide the Sight C on the Limb, ’till the Sun’s Rays passing thro’ it, likewise come thro’ the Sight A to the Eye. This being done, the Degrees of the Arc between B and C, shew the Sun’s Altitude.

But if the Sun’s Altitude is to be taken backwards, which is the best way, because of its Splendor offending the Eye, you must place the Eye to B, and looking thro’ the Sights B and A, at the Horizon, you must slide the Sight C along the Limb, ’till the Sun’s Rays coming thro’ it, fall upon the Sight A, and then the Arc BC will be the Sun’s Altitude above the Horizon, as before.

The Meridian Altitude or Zenith Distance of the Sun or Stars being found by Observation, to find the Latitude of the Place.

Having observed with some one of the Instruments before spoken of, the Meridian Altitude or Zenith Distance of the Sun, or some Star, seek the Sun’s Declination the Day of Observation: if it be North, substract the Sun’s Declination found from the Sun’s Altitude, and you will have the Height of the Equinoctial above the Horizon, and this Height taken from 90 Degrees, and you will have the Latitude of the Place. But if the Zenith Distance be added to the Declination of the Sun or Star, the Sum will be the Latitude of the Place.

Again, If the Sun or Star have South Declination, you must add the observed Altitude to the Declination, and the Sum will be the Height of the Equinoctial above the Horizon, which taken from 90 Degrees, and the Latitude will be had. But if the Zenith Distance be taken from the Declination, the Remainder will be the Latitude of the Place.

Lastly, If the Sun has no Declination, his Altitude taken from 90 Degrees, will be the Latitude; and so in this Case the Zenith Distance itself is the Latitude.

Example. The Sun being in the first Degree of Cancer, his Meridian Altitude at Paris is 64 Deg. 30 Min. Zenith Distance 25 Deg. 30 Min. his Declination 23 Deg. 30 Min. North. Now if 23 Deg. 30 Min. be taken from 64 Deg. 30 Min. the Remainder is 41 Deg. for the Altitude of the Equinoctial, and so the Complement of 41 Deg. to 90 Deg. is 49 Deg. the Height of the Pole or Latitude of Paris; but if the Zenith Distance 25 Deg. 30 Min. be added to the Sun’s Declination 23 Deg. 30 Min. the Sum will be 49 Deg. the Latitude of Paris as before.

Again, Suppose the 22d of December (New Stile) the Sun’s Meridian Altitude at Paris is observed 17 Deg. 30 Min. and his Zenith Distance 72 Deg. 30 Min. his Declination is then 23 Deg. 30 Min. South, which added to 17 Deg. 30 Min. and the Sum is 41 Deg. whose Complement 49 Deg. is the Latitude of Paris. Again, If from the Zenith Distance 72 Deg. 30 Min. be taken the Declination, the Remainder will be 49 Deg. the Latitude of Paris, as before.