Introduction
Astronomy is that science which teaches the distribution and arrangement of the various heavenly bodies, their true and apparent motions in space, their magnitudes and distances, their physical structure, so far as known, and their mutual influences, so far as these influences are indicated by observations and established by induction.
The high importance of this science is evident to every reflecting mind. Its elevated object needs only to be mentioned to awaken feelings of dignity and grandeur in the human breast; for the conceptions and ideas it arouses of the infinity of the universe, and of the power, wisdom, and goodness of the Creator, excite in otherwise insensible dispositions, feelings of astonishment, admiration, and reverence. The benefits which human society (man) has derived from Astronomy, particularly with regard to the more accurate determination and division of time, the perfection of distant navigation, the fixing of the geography of places, &c., have been of infinite importance. To every cultivated mind, the exact knowledge of the true connexion and relation of our planet to the universe, if not absolutely indispensable, is yet most useful and attractive: it elevates the reflecting mind above an undue estimate of the size and importance of the earth, by showing its insignificance in respect to the great whole; it enlarges the circle of ideas, calls to mind the infinite, the unchangeable, and awakens longings and hopes in the soul, whose realization and continuation beyond the stars may form one portion of future blessedness.
Astronomy is divided first of all into three parts. 1. Spherical Astronomy, which teaches the knowledge of the various points and circles of the celestial sphere, the constellations, the position of the stars with respect to these points and circles, as also the phenomena occurring in the sphere of the Heavens. 2. Theoretical Astronomy, which enables us to determine from observation the true paths of the heavenly bodies, particularly of the planets. 3. Physical Astronomy, which gives the laws by which the motions of the heavenly bodies are regulated, shows how these motions are to be calculated according to the rules of mechanics, and finally combines all that is known up to the present time, of the physical characters of the heavenly bodies.
Practical astronomy is to be considered as the basis of these three divisions, which together form theoretical astronomy. This may be divided into: 1. Observing Astronomy, which treats of the apparatus (instruments), and the observations made with it: 2. Calculating Astronomy, which teaches the method of obtaining from the observations the calculated results. For a well-grounded study of astronomy, a knowledge of pure mathematics, of mathematical physics, and of the sciences of optics and mechanics, is necessary. To become a practical astronomer, talent for observing, and a readiness in calculating, are required.
Astronomy, from its very nature, gives quite an abundant opportunity for pictorial representations, which have for their object either to explain theoretical propositions, or to make a visible exhibition of the objects and phenomena of the starry heavens. It might, however, be a not uninteresting preliminary, to take a historical survey of this science, showing how the investigating disposition of man has been occupied in its endeavor to obtain a more accurate and perfect knowledge of the Universe.
It is highly probable that the earliest nations, incited by the beauty of the starry heavens, and the necessities of life, gradually learned the changes of the days and seasons, the course of the sun, the moon, and some planets. The Chaldseans introduced the twelve signs of the zodiac, the sun-dial, and the clepsydra or water clock; and also laid the foundations of Astrology. The Persians and Babylonians determined the sun's year at 365\(\frac{1}{4}\) days; the Phoenicians applied Astronomy to navigation; and that the Egyptians possessed astronomical knowledge is abundantly shown by characters on their obelisks and temples. The Chinese seem to have known and used the gnomon from the most remote antiquity, and the Emperor Yao (2367 b.c.) determined the moon’s year to be 354 days. At the time of Hoang Ti, they were acquainted with the equinoctial and solsticial points. The Greeks, however, first raised Astronomy to a higher level: Thales (640 b.c.) knew the cause of eclipses of the sun and moon; Anaximander constructed a geography and the first map: and Meton introduced the moon’s cycle of nineteen years, to reconcile the moon’s year with the course of the sun. Aristarchus (born 267 b.c.) was the most celebrated astronomer among the Greeks; he even guessed at the motion of the earth around the sun. He was followed by Hipparchus, who, by means of the equinoxes, determined the sun's year to be 365 days, 5 hours, 55 minutes, 12 seconds; and also constructed a catalogue of fixed stars. Ptolemy likewise sketched out a catalogue of fixed stars, as also a system of the universe, called after him the Ptolemaic system. The Romans had too little taste for mathematics to become good astronomers: Seneca alone, with a few other Roman philosophers, had just ideas of the heavenly bodies; the Romans were, however, so much the more given to Astrology. Julius Caesar introduced the calendar invented by the Greek, Sosigenes, and called, after him, the Julian. Later than this, when learning fled to the newly established cloister, Astronomy was cultivated almost exclusively by the Arabians, particularly from a.d. 650. Albatari prepared astronomical tables; and in the time of Almansor, the moon's year was introduced, which is still in use among the Turks; but after the death of Almansor (in the 10th century), the study of Astronomy among the Arabians died away, and during the middle ages scarcely anything was esteemed but Astrology. Charlemagne, Gerbert (Pope Sylvester II.), the Emperor Frederic II., King Alphonso of Castile, and some others, make the only honorable exceptions by their active participation in the study. Alphonso the Tenth held at Toledo, in 1240, an astronomical convention, whose fruit was the Alphonsine tables. At a later period appeared the first European astronomers, properly so called, Vitello, Bonatus, Purbach, John of Gamundia (first rectifier of the calendar), and Regiomontanus (calculator of ephemerides). At the end of the fifteenth century, Savonarola and Picus of Mirandola earnestly contended against Astrology. All were, however, eclipsed by Copernicus, who, in 1508, presented to the world his theory, and its proofs, of the true arrangement of the planets in our system. Nevertheless he found many opponents, particularly Tycho Brahe, one of the greatest of practical astronomers. This latter individual defended the immobility of the earth, and presented another system of the planets, known under his name, which was, however, very soon overthrown by the celebrated laws of Kepler (1571–1630), who constructed the first tables (the Rudolphian), calculated according to the Copernican system. A contemporary of Kepler, Galileo, was in a measure the martyr of the Copernican theory, for he was obliged to renounce at Rome his belief in the double motion of the earth; this, however, could not hinder the spread of truth, since at this time the telescope was invented, by means of which an entirely new view of the universe was gained. The mountains of the moon were discovered, the phases of Venus, the moons of Jupiter, the spots of the sun, &c., all of which testified to the truth of the Copernican theory. Huyghens, the inventor of the pendulum, discovered a moon, and the true shape of the ring of Saturn. In the seventeenth century, Halley, Flamsteed, Hevel, and others, examined the heavens incessantly and accurately, and Newton was the immortal creator of Physical Astronomy, by his discovery of the law of gravitation. The delusion of Astrology now vanished, and there remained alone the fear of great comets. In the eighteenth century, Euler, Clairaut, and D’Alembert, worked out still further Newton’s Mechanics of the Heavens. Dollond invented the achromatic telescope, and, somewhat later, Herschel brought the Newtonian reflecting telescope to a wonderful degree of perfection: the discovery of the planet Uranus and his six moons was the result. A little before this, Mayer constructed his accurate tables of the moon. Bradley discovered aberration and mutation, and Lacaille, at the Cape of Good Hope, mapped out the southern hemisphere. Maupertuis, in Lapland, and La Condamine, in Peru, carried on measurements of a degree, in order to a more accurate determination of the size and figure of the earth; this end was, however, first obtained during the end of the last and the beginning of the present century, by the well known great French measurement of a degree. After Laplace and Lagrange had worked out in a masterly manner the theory of planetary perturbations, Burg, Burckhardt, Zach, Carlini, Lindenau, Bouvard, Damoiseau, and others, were enabled to construct their sun, moon, and planetary tables, which agree within a few seconds with the actual positions of those bodies. At the commencement of the present century, not a few comets were discovered by Olbers, Pons, Mechain, Huth, and others, as also the planets Ceres, Pallas, Juno, and Vesta, by Piazzi, Olbers, and Harding. Lalande, Bode, but especially Maskelyne and Piazzi, prepared fuller and more accurate catalogues of the fixed stars. Gauss taught new and very ingenious methods of accurately computing the planetary orbits, while Bessel attained the reputation of one of the greatest theoretical and practical astronomers that ever lived. During this time, however, the art of constructing astronomical instruments and achromatic telescopes was not behindhand, as the names of a Dollond, Ramsden, Troughton, Reichenbach, Fraunhofer, Repsold, and others, can satisfactorily testify. Finally, in later times, the appropriate and well arranged observatories at Altona, Berlin, Gottingen, Greenwich, Helsingfors, Konigsberg, Ofen, Paris, Pulkowa, Seeberg, Vienna, &c, have been erected, and three new planets discovered—Astrea, Neptune, and Iris—and the existence of a central sun has been indicated by Madler. Our century can point to a mass of accurate observations which have already been employed by theoretical astronomy to such account, that the science of the stars has been raised to a giant height, almost to entire perfection—a perfection which hardly any other branch of human knowledge can boast.
![]() Spherical Astronomy
Spherical Astronomy
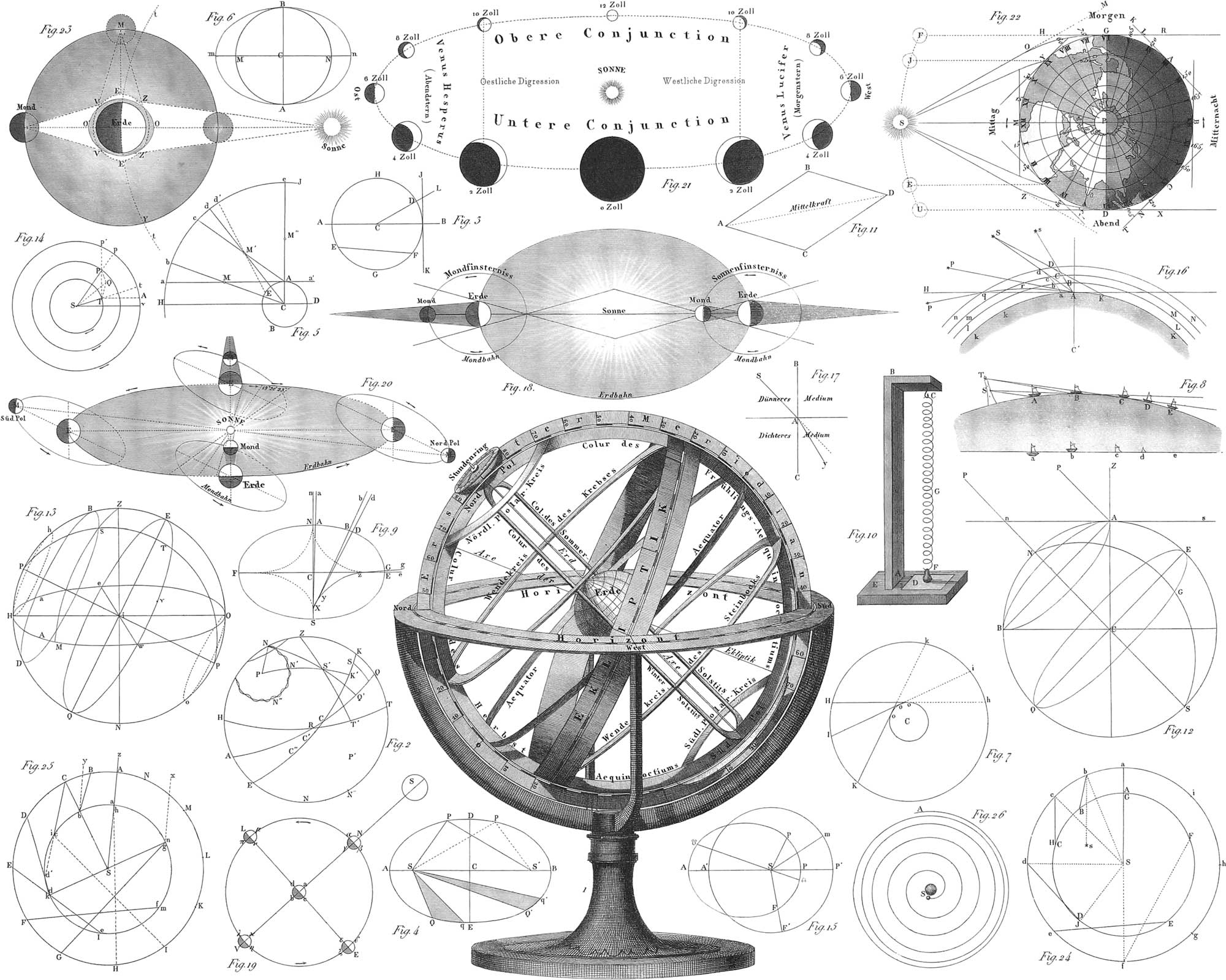
The Armillary Sphere; the most important Points, Circles, and Terms in the Celestial Sphere
The Armillary Sphere
1. The ancients at an early period imagined the existence of certain points, circles, &c., on the sphere of the heavens, by means of which they might the more readily comprehend, and be the better able to follow the various celestial phenomena. They also invented an instrument, the armillary sphere, partly with the view of giving an intelligible exhibition of the mutual relation of these points and circles, and of the axis of the heavenly motions, and partly to make actual observations by means of this sphere. The armillary sphere (pl. 6, fig. 1) consists of a frame, with a horizon on which are represented the 360 degrees, the regions of the heavens, the calendar, and the height of the sun for every day in the year. Two notches in the horizontal circle, and corresponding to its north and south points, receive the fixed meridian, whose plane is perpendicular to, and centre coincident with that of the horizontal circle. This meridian, within which the other circles as well as the small terrestrial globe may all be rotated together on the common axis of the heavens and earth, can be moved in these notches, still remaining in the original vertical plane; in this manner the general axis may be placed at various angular distances with the horizon. The centre of the small terrestrial globe is coincident with that of the general armillary sphere, the names and position of the other circles are evident from the figure without further explanation. The hour circle fastened to the north pole of the fixed meridian has a movable index, which, when fastened, revolves with the axis. The artificial sphere known as the celestial globe has the advantage over the armillary sphere in allowing the representation of the stars; but the latter exhibits to the senses far more clearly the relation of the most important points and circles of the celestial sphere to the inclosed terrestrial globe.
2. Fig. 2 gives likewise an explanatory representation of the most important points of spherical astronomy. The circle EHZT is the fixed meridian or noon circle; if its surface represent the western hemisphere of the celestial globe, then HRT is half the horizon, H its north, R its west, and T its south point. Z is the zenith, the visible highest point above the horizon, standing perpendicularly above the centre of the sphere, while N, the nadir, is the invisible lowest point below the horizon; the straight line ZN connecting these points is called the axis of the horizon, and corresponds to the direction of the plummet. The arc ACQ represents the semi-equator, ECK the semi-ecliptic (path of the sun). The equator ACQ passes through the east and west points (R) of the horizon. The point C, where the ecliptic and equator intersect, is called the vernal equinox. The spherical angle ACE, or KCQ, gives the amount of inclination of the ecliptic to the equator, that is, the obliquity of the ecliptic, 23° 27′, measured also by the arc AE or QK. The visible point N, everywhere 90° distant from the equator ACQ, is the north pole, the invisible one N″, directly opposite, is its south pole; the visible point, P, distant from N about 23° 27′, and 90° distant from every point of the ecliptic, is the north pole of the ecliptic, P′ its corresponding and invisible south pole.
Let S′ be the place of any star in the celestial sphere; and from the zenith Z, draw through the star S′ the arc ZS′T′ of a great circle, perpendicular to the horizon HRT, then the circle of which ZS′T′ is only the fourth part is the vertical circle of the star S′; and the arc T′S′ the altitude of this star, which is expressed in degrees, reckoning from the horizon; finally the arc ZS′ is the zenith distance. In the horizon the altitude is 0° and the zenith distance 90°, while in the zenith the altitude is 90°, and the zenith distance 0°. The arc TT′ of the horizon lying between the meridian and the quadrant ZS′T′ of the vertical circle passing through the star S′ is called its azimuth, also measured by the spherical angle T′ZT. The azimuth is reckoned from 0° to 180°, positively from the south point T, eastwardly as far as the north point H, and negatively from T to H, in the opposite direction by the west; as is very evident, the azimuth and altitude of a star completely fix its position in the celestial sphere with respect to the horizon.
If from the north pole, N, of the equator an arc, NS′Q′, be drawn through the star S′, perpendicular to the equator, the circle of which NS′Q′ is the quadrant is called the declination circle of the star, and the arc Q′S′ the declination. This is called north or south as the star is north or south of the equator, consequently as it stands in the northern or southern hemisphere of the heavens. The declination is estimated in degrees from the equator; at the equator being 0°, and at either of its poles 90°. The part CQ′ of the equator ACQ, lying between the vernal equinox C, and the declination circle NS′Q′ of the star S′, is called the right ascension of this star; it is reckoned from the vernal equinox C, around the equator from west to east, varying from 0° to 360° (or from to 24 hours), and is expressed in these degrees (or hours). By means, then, of the right ascension and declination of a star, we fix its position in the heavens for a long interval of time, with respect to the equator.
Draw from the pole, P, of the ecliptic, ECK, through the star S′, an arc PS′K′, cutting the ecliptic at right angles, then the great circle of which PS′K′ is only the quadrant, is called the circle of latitude of the star S′, and the arc K′S′, the latitude of this star. This is north when the star is above the ecliptic, as in the figure, and south when it is below. The latitude is estimated in degrees from the ecliptic; at the ecliptic it is 0°, at either pole 90°. The part CK′, of the ecliptic ECK, lying between the vernal equinox C, and the circle of latitude PS′K′ of the star S′, is called the longitude of the star. It is estimated on the ecliptic from west to east, and commences with the vernal equinox, expressed in degrees from 0° to 360°, or in terms of the 12 signs of the zodiac. The latitude and longitude of a star completely determine its position on the celestial sphere with respect to the ecliptic.
The arc HN of our figure represents the height of the pole N above the horizon HRT, that is, the altitude of the pole; and the arc TQ the height of the equator ARQ (on the meridian), above this horizon HRT, or the altitude of the equator. The altitude of pole and equator for the same place of observation, are together equal to 90°. The spherical angle Q′NQ, having the north pole, N, for its vertex, or the corresponding arc QQ′ of the equator, is called the hour angle of the star S′.
3. The following is a very satisfactory proof among many well known ones, of the spherical shape of the earth. Suppose an observer (fig. 8) stationed at a particular point, S, from which a ship sails off in a straight line. At a short distance the whole of the vessel will be visible to the water-line; with increasing distance the ship decreases in apparent height, but is visible to the water's edge. After reaching the horizon at B, there is not only a still further decrease in apparent size, but a disappearance of part of the vessel itself, beginning with the hull. At C only the sails and masts are visible; the appearance presented is represented by c. From a higher point T, however, whose horizon passes through D, the hull of the ship will be again visible. The distance still increasing, the lower sails seem just to sink into the water, as at d, and finally to disappear entirely. The distinctness with which the summits of the masts are observed, just before their disappearance, must carry home the conviction, that but for the intervening segment, ABCDE, of the sea, the actual distance, SE, is not so great as to prevent an equally perfect view of the whole.
The most important Points, Circles, and Terms of the Terrestrial Sphere
4. Spherical astronomy determines certain points and circles, as well on the terrestrial as on the celestial sphere. If, for instance, in fig. 12, C represent the centre of the earth, and NCS its axis of rotation, then, N, S, are the poles of the earth, QE the terrestrial equator, and AB the parallel of latitude of the place of observation, A, on the surface. Consequently the straight line, AP, parallel to SCN, is that direction in which the visible pole, P, of the heavens, is seen from the place of observation, A. The line AZ, a prolongation of a radius of the sphere, is the direction of the zenith from the observer at A. Furthermore, let NAES be the meridian of A; NGS, a fixed meridian, as the meridian of Paris; then, GE, or the spherical angle, GNE, is the (geographical) longitude of A, and EA, or the angle EC A, the (geographical) latitude. (For further particulars respecting geographical longitude and latitude, see Section 10.) Finally, if ns be a plane, tangent to the earth’s surface at A, it will constitute the visible apparent horizon of the place; and the straight line, nAs, produced by the intersection of this plane with the meridian, will be the meridian line of A, so that for A, n will be the north, and s the south pole of the horizon.
Miscellaneous Considerations respecting the Apparent Rotation of the Celestial Sphere, and the attendant Phenomena
5. A careful examination of the phenomena exhibited in the apparent daily rotation of the starry heavens, shows that in respect to this rotation, the size of the earth may be considered as entirely insignificant, that is, the observer can be supposed to be situated in the centre of the earth; an assumption very allowable when we reflect on the immense distance of the fixed stars from the earth. Let pl. 6, fig. 13, represent the celestial sphere, i, the observer, Z, his zenith, N, his nadir, then will the circle, HwOeH (whose poles are N and Z), be the celestial horizon; Pp represent the poles of the heavens, the circle, HZONH, the meridian, and HP, the altitude of the pole for the observer at i. This will be readily seen by referring to what was said on the subject in § 2. The circle, EwQeE, perpendicular to the axis, Pp, will be the equator, in which the vernal equinox occurs at ♈︎. Then, as already explained in fig. 2, the arc, ♈︎T (fig. 13), will be the right ascension, TS the declination, and PS the polar distance of the star, S, projected in the equator by the declination circle, PSTp; BD will also be the diurnal circle (parallel of declination) described by the star in its apparent motion about the pole, P. The circle, ZM, perpendicular to the horizon, is the vertical circle; the arc, HM, the azimuth; MS, the altitude, and ZS the zenith distance of the star, S. Finally, the points, H, w, O, e, are respectively the north, west, south, and east points of the horizon.
If Hh and Oo represent small parallels of declination, touching the north point of the horizon at H, and the south point at. O, then HA will be the circle of perpetual apparition, between which and the visible pole P the stars never set; and Oo, the circle of perpetual occultation, between which and the invisible pole p the stars never rise. All stars situated between these two circles will be sometimes visible and sometimes invisible. Thus, the star S will be seen when in that part, ABa, of its diurnal circle above the horizon, and will be invisible when in the portion ADa. Furthermore, the same star will, in the diurnal rotation of the heavens, come back to the same meridian every twenty-four hours, and consequently as the daily rotation of the heavens is uniform, the interval of sidereal time between the arrival of the star at the meridian of two different places, may be expressed by the difference of longitude of the two places. On the other hand, the interval expressed in the sidereal time between the arrival of two different stars at the same meridian, is measured by their difference of right ascension, so that here we find one reason for dividing the equator into both degrees and hours. We find, also, from an inspection of figs. 13 and 2, pl. 6, that the altitude of the pole at any place is its geographical latitude, and that the sum of the altitudes of the pole and the equator is always for the same place equal to 90°. Likewise we find that every star attains the greatest height above the horizon at its culmination, and that all stars lying within the circle of perpetual apparition, cross the meridian twice above the horizon, once above the pole, and once below it; the one being the upper culmination or transit, the other the lower.
The Apparent Course of the Superior and Inferior Planets
In the Copernican system, the inferior planets, Mercury and Venus, which are nearer the sun than the earth, are distinguished from the superior, Mars, Vesta, Astraea, Juno, Ceres, Pallas, Jupiter, Saturn, Uranus, and Neptune, which are more remote. This distinction is very proper, as the phenomena attending the courses of the inferior and superior planets, are in many respects essentially different from each other. The reason is, that we view the planets from our earth, which itself revolves around the sun at a different rate from the rest, and therefore we see them at very different distances. We observe therefore not the true, but the apparent courses of the planets, which will now be explained. It must ever be kept in mind, however, that the fixed stars being at almost an infinite distance from our earth, their rays must always reach it in parallel lines. In the first place, to illustrate the apparent course of an inferior planet, let ACEG, in fig. 24, represent the orbit of Venus, acegi that of the earth, and S the sun. Since the distance of Venus from the sun is about three-fourths that of the earth, and since she traverses her orbit in 7\(\frac{1}{2}\) months, then, if in fig. 24 we divide her orbit into 5, and that of the earth into 8 equal parts, one of these will represent the space traversed by each in 1\(\frac{1}{2}\) months. If, when Venus is at A, the earth is at a, the former is said to be in inferior conjunction with the sun (♀ ☌ ☉), that is, on the same side of the sun with the earth. Her apparent diameter is here the greatest, although actually invisible (fig. 21); at the expiration of three-fourths of a month, Venus is at B, and the earth at b. The former has consequently retrograded, since, taking the fixed direction of the star s as a line of reference, Venus to the observer on the earth appears to the right of the star, which is seen in the direction bs, parallel to As. It is also evident that Venus has become a morning star, since when the observer at b looks towards the sun, he sees the planet on the right of the sun. Hence Venus is seen in the eastern horizon before the rising of the sun. Pl. 6, fig. 21, represents her at this time, crescentic, and with two digits illuminated.
A month and a half after inferior conjunction, the fixed star in whose vicinity Venus was seen when the earth was at b, will be seen in a direction parallel to Bb, from the earth at c; consequently Venus will be seen in the direction Cc, to the left or eastwardly of this star. Hence, it follows that the apparent motion of Venus has again become direct. It will also be seen from fig. 24, that the angle scS, formed by lines drawn from the earth to the sun and the planet, is larger than the former angle, SbB; we accordingly say that the elongation of Venus has increased. The illuminated part of her disk has (as seen in fig. 21) increased to about four digits; her apparent diameter, however, sensibly diminishes. This elongation must be greatest at the time when the earth (fig. 24) is at d, and Venus at D, which is the case about 2\(\frac{1}{2}\) months after inferior conjunction; and this greatest elongation is equal to the angle DdS. Venus then (fig. 21), like the moon in her last quarter, has half of her disk, or six digits, illuminated.
Half a year after inferior conjunction, when the earth is at f, Venus will have reached F, consequently the elongation of Venus has again become less, since the angle, SfF, expressing this elongation, is evidently less than the angle SdD. Venus, then, during this time has approached the sun, has become fuller (fig. 21), but nevertheless smaller, although still the morning star (fig. 24). Three months after, the earth is at h, and Venus at H; the latter has therefore reached superior conjunction, that is, is on the opposite side of the sun from the earth. Her apparent diameter is now the least, and her entire disk (fig. 21) illuminated, although invisible. At a later period she appears in the evening sky as the evening star, and exhibits the same phases (fig. 21) as before, but in an inverted order. Her apparent diameter also increases.
To illustrate the course of a superior planet, let S (fig. 25) represent the sun in the centre of the earth’s orbit, abcdefgh. Let that of Mars be ACEGJLN. The earth revolves in twelve, and Mars in about twenty-three months. about the sun. If, therefore, the original positions of the earth and Mars were at a and A, at the expiration of 1,2, 3, 4, &c., months, the earth will have reached the points b, c, d, e, &c.; and Mars B, C, D, E, &c., respectively. When the earth was at a, and Mars at A, the latter was in opposition to the sun (♂ ☍ ☉), and the stars in the vicinity of Mars must show themselves in the direction az. The motion of all the planets from A to B is called direct; consequently Mars has a direct motion when advancing from the stars observed in the direction az, towards the left, and a retrograde motion when moving towards the right. Pl. 6, fig. 25, shows also that when the earth goes towards b, and Mars towards B, the motion of the latter must be retrograde, because he is observed to the right of the stars at z, seen in a direction, by, parallel to az. Therefore Mars, at the time of opposition, retrogrades.
After the earth has arrived at b, Mars is at B, and consequently no longer exactly opposite to the sun, S; but as the stars seen in the direction by culminate about midnight, he will then have passed the meridian and will be near his setting, and consequently will be seen in the evening sky.
Two months after opposition, the earth being at c, and Mars at C, the retrograde motion of the latter will have ceased, since the straight lines connecting b, B and c, C, are nearly parallel; consequently to an observer at the earth, the planet will appear stationary for some days. At a later period the motion of Mars will be direct. Two months later, Mars, still moving direct, will be at D, and the earth at d, so that now the lines c C, d D, form the angle Cd′D. It is evident that the directions dS, dD, from the earth to the sun and to the planet, form nearly a right angle to each other, and consequently that about this time Mars at sunset must be near the south, and must set about midnight.
At the end of the tenth month, when the earth is at g, Mars has not completed half his apparent course in the heavens, as shown by his not having reached a point opposite to the stars seen in the direction gx. The distance of Mars from the sun, however, is apparently only the angle GgS; as at this time an observer at g, looking towards the sun and planet, sees the latter to the left or eastward of the former. Mars must appear in the evening sky, after sunset, and evidently much smaller than at time of opposition.
At the expiration of a full year, the earth being at h, and the planet at H, the straight line, hH, shows that Mars has completed rather more than half the apparent circuit of the heavens, since the stars in the direction z stand nearly opposite to him. Consequently the conjunction of Mars with the sun (♂ ☌ ☉) has not yet taken place, as, from an inspection of fig. 25, it will be seen that the sun still appears to the right of Mars or H.
Two months later Mars is seen early in the morning sky, for since from i, the position of the observer, the planet is seen to the right of the sun, at I, he must evidently rise before the sun. By continuing this consideration, with f he assistance of fig. 25, we shall soon find that Mars, shortly before his new opposition, again becomes retrograde, and that the phenomena before observed must all succeed each other again in the same order.
From all that 'has preceded it follows, without further explanation, that the inferior planets have an inferior and a superior conjunction, but no opposition; that the superior planets have a conjunction and an opposition, never two conjunctions; and, finally, that while the inferior planets are never visible in the heavens at midnight, the superior may be seen at any hour of the night.
The Moon; her Revolution around the Earth; Phases of the Moon; the Moon’s Nodes
7. Our earth, in her yearly course about the sun, is accompanied by a satellite, the moon, which revolves around the earth in about a month., and in little more than four weeks wanders through the whole zodiac. We need only observe the moon for a few hours, on several successive clear evenings, to satisfy ourselves that while, with the other stars, she follows the diurnal motion from morning till night, she has a peculiar motion of her own, from west to east, advancing daily a little over 13 degrees among the fixed stars of the zodiac. This peculiar motion of the moon is the result of her revolution about the earth; and for the same reason, being an opaque body illuminated by the sun, she is exhibited in all possible shapes (phases). The four principal of these are, the new moon, the first quarter, the full moon, and the last quarter. The new and full moon are known as the syzigies; the first and last quarters as the quadratures. Pl. 6, fig. 19, offers an intelligible illustration of the various phases of the moon, depending on her different position with respect to the sun and earth. Let abcd be the earth placed in the middle of the moon’s orbit, NEVLN, and S the sun, whose distance, Sa, from the earth is supposed to be so great that all his rays are parallel to the line SNV. Let the moon be at Nβγα, or between the earth and sun, her dark side, βγα, will then be turned to the illuminated side (dac) of the earth. At this time the moon is new, and being above the horizon in the day time, is invisible. Compare pl. 10, fig. 5. Two or three days after this time, the moon, moving in her orbit in the direction of the arrow (fig. 19), is seen soon after sunset, in the evening sky, as a narrow crescent, which soon sets. This crescentic shape of the moon becomes broader, and she sets later every day, and removing constantly from the sun, she shines through the first hours of the night. In about seven days the moon will have reached Lπνμ, or the first quarter, and to an observer at d, or the boundary between day and night, will be seen to the left of the sun, as a semicircular disk, with the straight edge to the left or east: the moon now culminates about six o’clock in the evening (see pl. 10, fig. 5), and sets about midnight. From this time, the outline which from new moon to the first quarter was concave, becomes convex; the moon shines longer, and sets after midnight. In about seven days she will have reached Vλκη, and become full, standing directly opposite the sun, behind the earth; her illuminated half, λκη, consequently, to the dark side, dcb, of the earth, appears as a full circle, which rises in the east as the sun sets in the west, culminates at midnight, and sets in the west at sunrise. The moon now rises about an hour later each night, and gradually loses the illumination of her right or westerly side, so that the circular disk becomes oval, until, in seven days after full moon, she will have arrived at Eζεδ, or the last quarter. To the observer at c, the boundary between night and day, her illuminated side, Eεδ, appears as a half disk, to the left or west of the sun, and the line separating the dark and the illuminated portion will be on the west side, while in the first quarter it was on the east. At the last quarter, she rises about midnight, and crosses the meridian at about 6 o’clock in the morning. Her semicircular disk now begins to become narrower, the straight edge concave, and the moon again assumes, as she approaches the sun, a crescent shape, which is smaller as the interval of time between the rise of the moon and that of the sun diminishes. About seven days after the last quarter, the moon entirely vanishes, again reaching Nβγα, her position about four weeks before. She now becomes new moon afresh, rising and setting with the sun, and her phases follow in the same succession.
8. Since our earth is also an opaque globe illuminated by the sun, we must present the same alternation of phases to an observer at the moon, that the moon presents to us, only in an inverted order. At the time, therefore, of new moon, first quarter, full, and last quarter, our earth must be full earth, last quarter, new earth, and first quarter.
The moon, during a revolution around the earth, describes an orbit, cutting the apparent path of the sun (the ecliptic), or the orbit of the earth, to which it is inclined about 5° 8′ 48″, in two points called the moon’s nodes (pl. 6, fig. 20). The point in which the centre of the moon cuts the ecliptic in passing from the south to the north, is called the moon’s ascending node, ☊, or the head of the dragon; and the one produced in passing from north to south, the moon’s descending mode, ☋, or the dragon’s tail. The distance of the moon from the ecliptic is called the latitude, which may be north or south. At the nodes, the latitude is 0°; hence it follows that the sun, moon, and earth (the sun and earth being in the same plane), must lie at all times nearly in the same plane (fig. 20), and when the moon is in one of her nodes, that is in the ecliptic itself, then the three bodies—sun, moon, and earth—have their centres in the same straight line.
The ancients observed that the moon’s nodes did not remain in the same part of the ecliptic, but continually moved backwards, or from east to west (indicated in fig. 20 by the dotted lines). This retrogression takes place in the following manner: one of the nodes of the moon’s orbit—the ascending, for instance—retrogrades in such a manner that if it had coincided with the new moon at starting, this coincidence would again happen after an interval of 18 years and 11 days. The moon’s node will then be still 11 degrees distant from the position assumed 18 years and 11 days before. But the sun has in the meantime advanced 11 degrees, and consequently stands again in the node; therefore, since the moon is again in the new moon, an eclipse of the sun must occur, just as it did 18 years, 11 days before. However, the coincidence of the new moon with the node does not take place exactly in the same manner. These periods of 18 years and 11 days, supposed to have been called Saros by the Chaldsean astronomers, are known as the periods of Halley, and were employed by the ancients in the prediction of solar and lunar eclipses. The retrogression of the moon’s nodes is a consequence of the secular perturbations of the moon’s orbit, and at a mean, with reference to the fixed stars, amounts annually to 19° 20′ 29″ (pl. 6, fig. 20).
The Seasons; Daily and Yearly Motion of the Sun
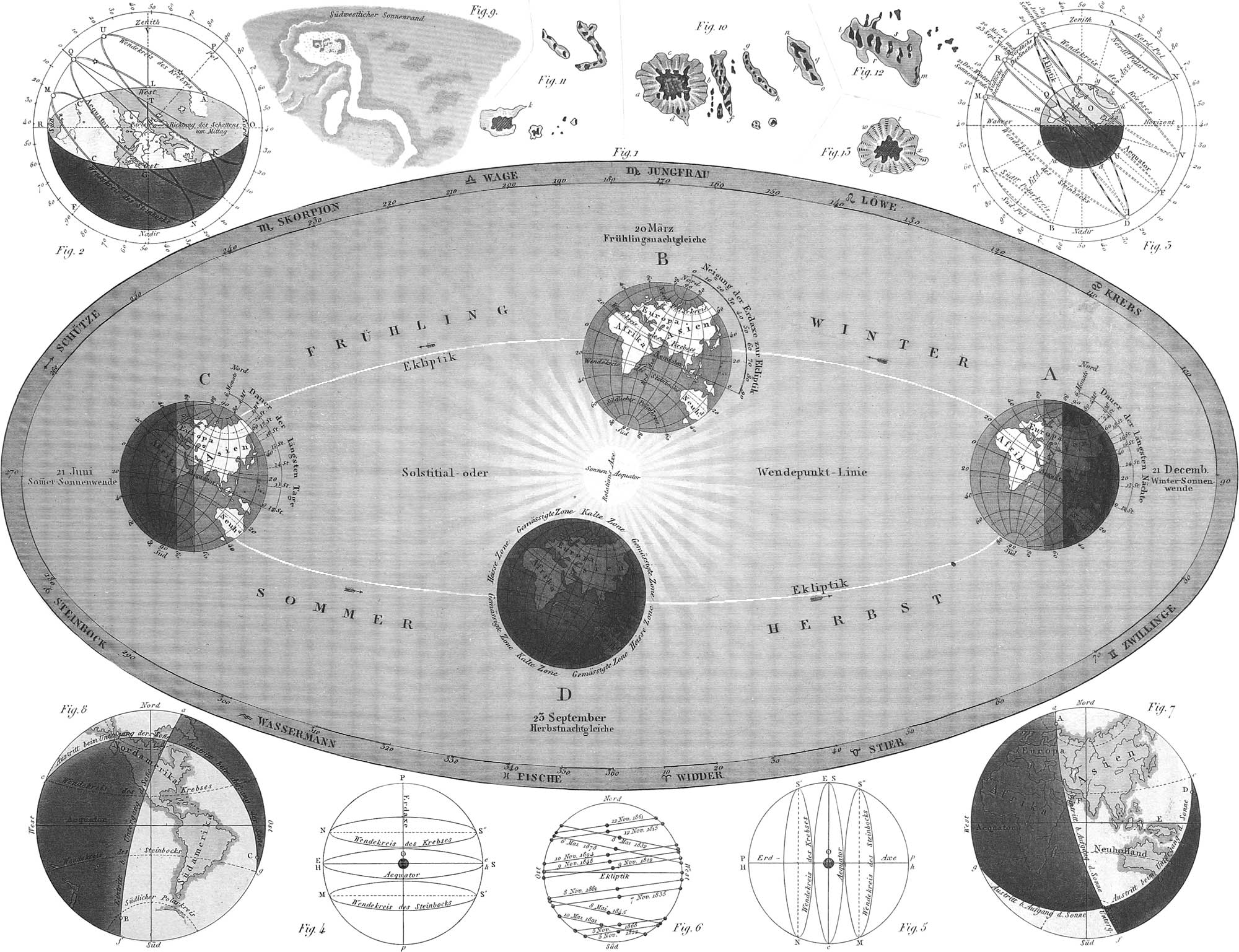
9. The illustration on pl. 9, figs. 1, 2, 3, serves to elucidate the theory of seasons, and of the daily and annual motion of the sun. The following may be taken in connexion with what is said further on (sect. 26) respecting the annual motion of the earth round the sun.
The visible horizon is that circle in whose centre we are supposed to stand, and which bounds our vision, and upon which the heavens appear to rest. The sun is said to rise in the morning when it appears above the horizon, as at C, pl. 9, fig. 2, and to set in the evening when sinking below the horizon, as at C′. The sun appears each day to describe a greater or less circular arc, CMC′, above the horizon, and this arc is constantly inclined towards the horizon. Noon of a place is that time of day when the sun at M has arrived at its greatest height above the horizon. The vertical of a place (Paris in fig. 2) is the straight line VT, parallel to the direction of the plumb line. The line RSO is the meridian line of Paris, or the direction of a shadow at time of noon at Paris; the four points, O, G, R, L, are the four cardinal points of the horizon. The sun appears to traverse a part, CMC, of a circle by day, completed at night in C′NC. beneath the horizon, and the entire apparent circuit of the sun about the earth lasts 24 hours, or an entire day. A careful examination will, however, disclose the fact that the points of rising and setting of the sun, as also those in which he cuts the meridian, vary from day to day, with respect to the horizon of one and the same place. Thus, on 21st December, CMC′ is the day circle of the sun; GQL that of the 20th March, greater than the preceding, and KUA that of the 21st of June, which is greatest of all. Hence the sun appears to remain stationary for a time, and then to return towards the south, describing anew the arc GQL to the 23d of September, and CMC′ on the 21st of December, as before. Here he appears stationary for a time, and then returns to the north as before. These arcs described by the sun are all parallel to each other: the greatest of them, KUAK (towards the north) is called the tropic of Cancer, the least, CMC′NC (to the south) the tropic of Capricorn. The two periods of the year in which the sun describes the tropics are called the solstices. The circle described on the 23d September and the 20th March is called the equator, and the two periods when the sun describes the equator are called the equinoxes. Consequently the sun seems to move north for six months in the year, viz. from December 21st to 21st June, and south for six months, from 21st June to 21st December.
There is still another motion observable in the case of the sun, viz. a daily progression eastward of about a degree, while the fixed stars retain their relative positions unchanged. Since now 1° in space answers to four minutes in time, the sun will return to the same point of the heavens four minutes later each day, which in 90 days will amount to six hours. The imaginary straight line, PF, passing through the centre, S, of the horizon, and about which the sun appears to describe his circles, is called the axis of the heavens. Since all parallel circles of the sun are inclined to the horizon, and the axis of the heavens is perpendicular to their planes, the axis itself will be inclined to the horizon at the angle PSO, or the arc PO. Their two extremities, P, F, are called the poles, P being the north pole, F the south. From the preceding it follows, that for all planes between the equator and the poles of the earth, the celestial sphere is oblique (pl. 9, fig. 3), since the equator, the parallels of declination, and the axis of rotation, have an oblique situation with respect to the horizon.
If the observer be situated at the north pole (fig. 4). O, then the celestial sphere becomes to him parallel, since there the equator and the tropics, as seen in fig. 4, are parallel to the horizon. The axis Pp of the horizon coincides with the axis of the sphere Pp, and the horizon Hh with the equator Ee. Should the sun be situated in the plane of the equator, he will describe the circle SH, or the horizon, his disk being half above and half below it. When, after the expiration of three months, the sun has reached the tropic of Cancer at S″, he will describe the circle S″N, 23° 27′ above the horizon. He will now be evidently above the horizon, and, in fact, so remain for three months longer, gradually returning to the equator. Thus at and about the north pole the day is six months long. As a matter of course the region about the south pole of the earth must have an equal length of night. During the other six months of the year, these conditions are reversed for the two poles. The fixed stars, however, of these regions never set, that is, those of the northern heavens at the north pole, and those of the southern heavens at the south pole, since they describe their circles parallel to the horizon.
Fig. 5, pl. 9, shows the position of the points and circles of the celestial sphere to the observer at the equatorial regions of the earth. There the two poles, P, p, lie in the horizon, Hh, and consequently the axis, Pp, zenith, E, and nadir, c, in the equator. The planes of the equator and tropics are perpendicular to the plane of the horizon, whence the celestial globe forms a right sphere. The fixed stars all rise and set perpendicularly to the horizon; each one remaining visible for 12 hours, and invisible for a like portion of time. It is very evident that, in the region of the equator, all the fixed stars must gradually come in sight, and that whether the sun describe the circles, S, S′, or S″, they will all be divided into two equal parts by the horizon. In consequence of this, throughout the whole year at the equator, the days and nights will be equal, and of 12 hours each.
The Geographical Latitude and Longitude of a place; Determination of these
10. An accurate knowledge of the geographical latitude and longitude of a place, that is, its geographical position upon the earth, is of vast importance to mathematical geography and navigation. The geographical latitude of a place is the shortest distance of the place from the equator, expressed in degrees, minutes, and seconds. It will, therefore, be northern or southern, as the place lies north or south of the equator. If, through the given place and the axis of the earth, we pass a great circle, cutting the equator at right angles, it will be the circle of latitude of the place, and that part of the circle intercepted between the place and the equator, will be its geographical latitude, which may consequently range from 0° to 90°. Any place at the equator has a latitude of 0°; at the poles the latitude will be 90°. Now, as the altitude of the poles is equal to the latitude of the place of observation, we know the one when we know the other. For the determination of the altitude of the pole, a knowledge of the mutual situation of the zenith and pole, with reference to the horizon and equator, is necessary, and this can only be obtained by measurement of the altitudes of certain stars. In practice, therefore, the determination of the altitudes of the pole will depend upon the accuracy with which this measurement can be effected. Various methods have been devised to meet the wants of observation, as also the uncertainties which result from the declination of the star employed, its parallax, and refraction, so that the following eight methods of determining polar altitudes have been suggested and followed.
1, By the meridian altitude of the star; 2, by circummeridian altitudes; 3, by two culmination altitudes at the superior and inferior transits across the meridian; 4, by two meridian altitudes in the southern and northern parts of the meridian; 5, by the altitude of the polar star; 6, by equal altitudes of the circumpolar stars; 7, by altitudes of two stars and the observed interval of time; 8, by the observation of a star in its passage through the eastern and western part of the prime vertical.
The geographical longitude of a place is the arc of the equator intercepted between the circle of latitude of the place, and the circle of latitude of another place, assumed as a fixed point of reference. The latter circle of latitude is then called the first meridian, and the former the meridian of the place whose longitude is to be determined. Since nature indicates no definite line or circle of departure for the determination of longitude, as she has done in the equator for the determination of latitude, it is evident that the position of the prime vertical, and consequently the amount of the longitude, must be entirely arbitrary. This uncertainty has had for its consequence, the assumption of various standards, inconvenient in practice, and very often producing mischievous effects upon the interests of navigation, which, although now palliated, have not been entirely removed. The difference in the estimate of longitude has, however, been hitherto still greater among astronomers than among navigators, although a difference in estimating the longitude among the former, where calculation is appealed to for assistance, is much less troublesome than among the latter. Almost every astronomer counted the geographical longitude from his own observatory. The meridian of Paris has, however, more recently been selected by the astronomers of the continent of Europe, to which almost all observations and geographical longitudes are referred. It is generally customary in astronomy, at the present time, to regard only the meridian difference of two places of observation, or the angle which the meridian or noon circles of the two places bear to each other, at the pole lying nearest to them. This angle is, of course, measured by the arc of the equator lying between the two meridian circles. This difference of geographical longitude is often called the meridian difference of two places, since it is equal to the difference of time given by two clocks keeping true time, at the respective places of observation. This difference expressed in hours, minutes, and seconds, is converted into degrees, minutes, &c., by being multiplied by 15, and then will be equal to the above-mentioned angle formed by the two meridian circles at the pole, or the arc of the equator contained between these circles.
The measurement of the distance of two meridian circles, however involves greater difficulties than the determination of the altitude of the pole. The meridian difference of two places is determined by the time required by a star, in the course of its apparent daily revolution, to pass from the meridian of the eastward place to that of the western. Should this star be the sun, we can only compare the times which the clocks in the two places show at one and the same moment. For since at each place the clocks are set 0, or 12, at the time the sun passes his meridian, these, if they keep accurate time, must always differ by the same number of hours, minutes, and seconds. There is therefore only needed some means by which the clocks and instruments used at the different places of observation may be compared with each other, and this may be done in two ways; first, by carrying one clock to the other, without changing their rate in the least; or, secondly, by observing the clock time at which some phenomenon visible from both places, and determinable to the seconds, takes place. The difference in time obtained by either of these methods is then the desired meridian difference, or the difference in longitude, of the two places. We may also remark that the first method consists in the employment and application of portable clocks or chronometers. The second, however, consists in the observation, a, of eclipses of the moon and of Jupiter's satellites; b, of occultations; c, of eclipses of the sun; d, of corresponding culminations of the moon and neighboring fixed stars; e, of lunar distances; and f, of gunpowder or other artificial signals. It is not our place here, to go over these different methods separately and circumstantially, nor to explain the mode of calculating the meridian difference desired. It must suffice to examine a little more closely one, and indeed a very simple method, namely, to show how from observations of the eclipses of one of Jupiter’s satellites in two places, the difference of their geographical longitude can be obtained. Let, for instance, in pl. 10, fig. 1, E be the place of one observer, V that of another, both points being on the surface of the earth. Let both observers note by their clocks the time of their place at which the eclipse of any one of Jupiter’s satellites takes place, that is, the time when the satellite begins to enter the cone of shadow ending at x. We will now assume that the time at E is 8 o’clock and the time at V is 10 o’clock, the difference of these two periods amounts to 2 hours 30°, therefore V is 30° east of E.
Unfortunately, the moments (beginning and end) of an eclipse of one of Jupiter’s satellites cannot be so readily determined as that of the moon, on account of the unequal illumination and magnifying power of the different telescopes, as also the different acuteness of vision of different observers. Consequently, the meridian difference deduced will not be accurate, or at any rate not reliable; while the other methods admit of greater precision.
The Fixed Stars; their Size, Number, Arrangement, and Distances
11. By fixed stars is to be understood all those stars which are neither planets, nor moons, nor comets, deriving the name from the fact of never changing their relative positions when viewed with the naked eye. The fixed stars are the most numerous objects in the heavens, and are divided into eight classes, according to their various apparent sizes and brilliancy. We speak, for instance, of stars of 1st, 2d, 3d, 4th, 5th, 6th, 7th magnitude, so that those of the 1st magnitude possess the greatest brilliancy, and those of the 7th are only visible to the very acute naked eye. To the 8th class, that is, to those of the 8th, 9th, 10th, &c., magnitudes, belong all those millions of stars which are only visible through the telescope, hence called telescopic stars. The color also, especially in the double stars, is very various.
Although the fixed stars do not change their relative positions to each other, yet they have a common apparent motion, produced by the actual daily rotation of the earth on. its axis; in addition to this, the annual revolution of the earth about the sun produces various differences in their position with respect to the sun. Finally, there are other although very minute variations in the position of the stars with respect to the horizon, the equator, the ecliptics, &c., produced by refraction, parallax, precession of the equinoxes, nutation, &c, which will be referred to hereafter.
As the number of the stars is apparently infinite, it must necessarily be impossible for us ever to estimate it. Nevertheless, many astronomers have attempted to determine this approximately, at least with respect to the visible stars. The number of those of the first magnitude is 14, of the second, 70, of the third, nearly 300; that of stars of the 4th and succeeding magnitudes is much greater. The fixed stars stand so close together in many parts of the heavens, that any enumeration of these would be absolutely impossible. We need only examine the milky way through a good telescope, to discover that it consists of an innumerable number of fixed stars. Herschel at one time saw more than 50,000 stars cross the fixed field of his great reflector in a space of 30 degrees, near the club of Orion: at another time, he observed 258,000 to pass his 20 foot reflector in 41 minutes.
Lambert, in his “Kosmologische Briefe,” was the first to treat of the distribution and arrangement of stars in the heavens. It is in more recent times, however, since the discovery by Madler of the central sun of our system of fixed stars, that the first tolerably satisfactory explanation of the arrangement of the stars has been given. With respect also to the distances of the stars, nothing more definite was known than that the nearest of them was so remote as to require six years for its light to reach our earth. Bessel and Struve, however, by means of observations of the particular motions exhibited by the double stars 61 Cygni, and Vega (α) Lyræ, have determined these distances with approximate accuracy. According to Bessel’s investigations, the distance between our sun and star 61 Cygni would be traversed by light within ten years.
12. Besides the division of stars according to their apparent size, they are classified as single, double, and multiple stars, variable and temporary stars, and nebulous stars. These will all be referred to hereafter. Groups of stars which are visible, partly to the naked eye, partly by means of the telescope, are called constellations; while those in which, even with the aid of the most powerful telescope, the individual stars cannot be made out, the whole appearing as a light nebulous cloud, are called nebulæ. Finally, that belt of light formed by innumerable stars, and encompassing the whole heavens, varying in breadth and concentration, exhibiting sometimes one branch, and sometimes two, is called the milky way. This passes through the constellations (pls. 12, 13) Cassiopeia, Perseus, Orion, Gemini, Argo, Centaurus, Ara, Scorpio, Sagittarius, Ophiuchus, Aquila, Cygnus, and Cepheus. Its two branches unite in Ara and Cygnus.
The Constellations
13. For the sake of assisting the memory in recollecting the general distribution and relations of the stars in the sky, they have been divided into constellations. Those of the northern hemisphere are represented in pl. 12, those of the southern in pl. 13. These constellations are groups of fixed stars, whose outlines have been supposed to represent figures of men, animals, and other objects, and to which corresponding names have been given. With the arrangement of new constellations, it becomes necessary to have new names, which may either be derived from the animal kingdom, as done by the ancients, e. g. the Giraffe and the Lizard, or names may be selected commemorating important discoveries and inventions in the arts and sciences, e. g. the compass, the air pump, and the pendulum clock.
The names of the separate constellations, as given by Hipparchus, are the following:—
The Twelve Constellations of the Zodiac
- ♈︎ Aries, (Ram,) Widder.
- ♉︎ Taurus, (Bull,) Stier.
- ♊︎ Gemini, (Twins,) Zwillinge.
- ♋︎ Cancer, (Crab,) Krebs.
- ♌︎ Leo, (Lion,) Löwe.
- ♍︎ Virgo, (Virgin,) Jungfrau.
- ♎︎ Libra, (Balance,) Wage.
- ♏︎ Scorpio, (Scorpion,) Skorpion.
- ♐︎ Sagittarius, (Archer,) Schütze.
- ♑︎ Capricornus, (Goat,) Steinbock.
- ♒︎ Acquarius, (Water Bearer,) Wassermann.
- ♓︎ Pices, (The Fish,) Fische.
The Twenty-one Constellations of the Northern Heavens

- Cassiopeia, (Cassiopeia,) Kassiopeia.
- Andromeda, (Andromeda,) Andromeda.
- Triangulum, (Triangle,) Nödliches Dreieck.
- Perseus, (Perseus,) Perseus.
- Auriga, (Charioteer,) Fuhrmann.
- Ursa Major, (Great Bear,) Grosser Bär.
- Draco Borealis, (Dragon,) Nödl. Drache.
- Bootes, (Bootes,) Bootes.
- Coronoa Borealis, (Northern Crown,) Nödl. Krone.
- Cepheus, (Cepheus,) Cepheus.
- Pegasus, (Pegasus,) Pegasus.
- Ursa Minor, (Lesser Bear,) Kleiner Bär.
- Hercules, (Hercules,) Hercules.
- Ophiucus, or (Serpentarius,) Ophiucus.
- Serpens, (Serpent,) Schlange.
- Lyra, (Lyre,) Leier.
- Aquila, (Eagle,) Adler.
- Cygnus, (Swan,) Schwan.
- Sagitta, (Arrow,) Pfeil.
- Delphinus, (Dolphin,) Delphin.
- Equuleus, (Little Horse,) Kleines Pferd.
The fifteen Constellations of the Southern Heavens
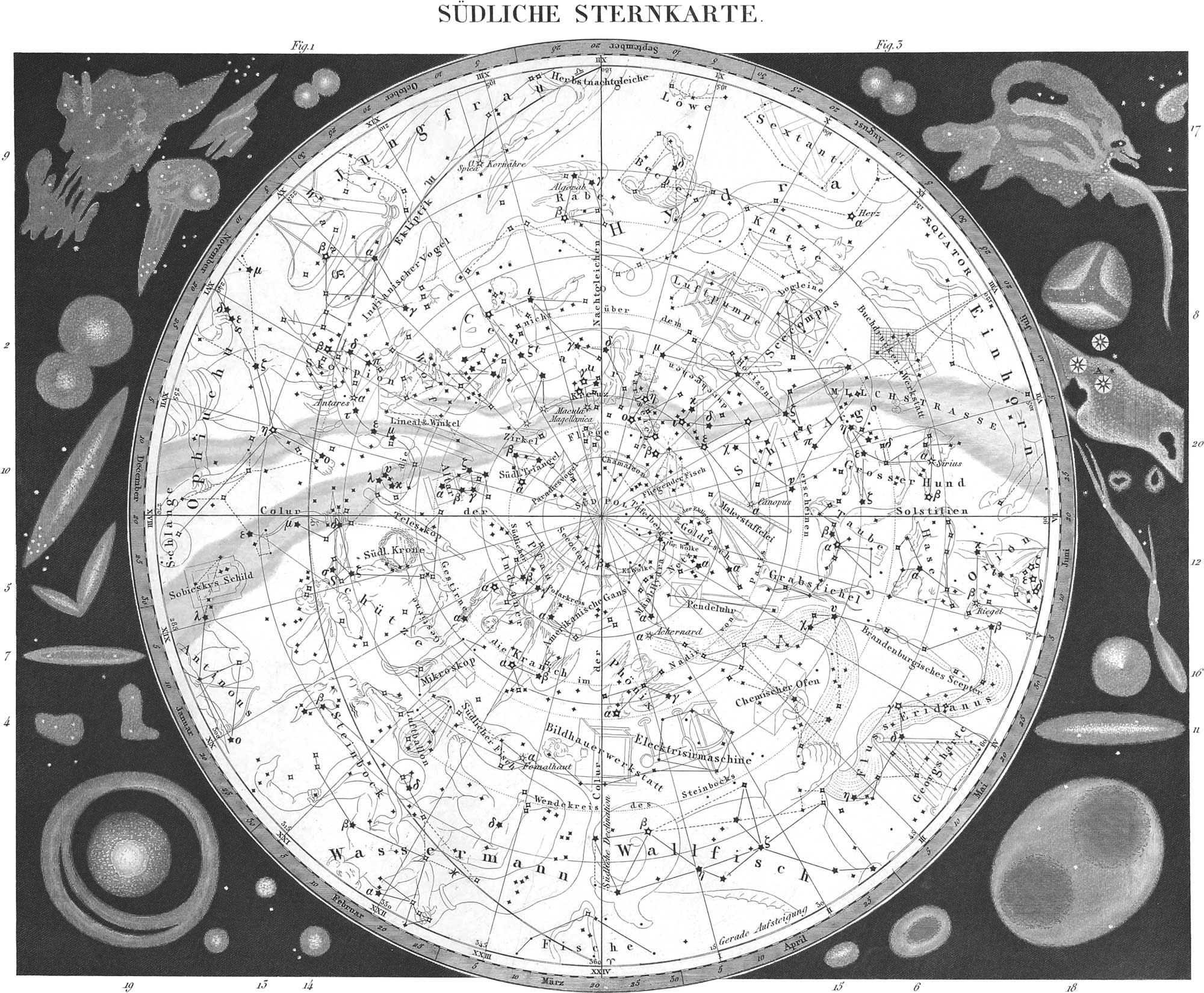
- Cetus, (Whale,) Wallfisch.
- Canis Major, (Great Dog,) Grosser Hund.
- Canus Minor, (Little Dog,) Kleiner Hund.
- Hydra, (Hydra,) Grosse Wasserschlange.
- Crater, (Cup,) Becher.
- Corvus, (Crow,) Rabe.
- Lupus, (Wolf,) Wolf.
- Orion, (Orion,) Orion.
- Centaurus, (Centaur,) Centaur.
- Argo, (Ship,) Schiff Argo.
- Corona Australis, (Southern Crown,) Südliche Krone.
- Piscis Australis, (Southern Fish,) Südlicher Fisch.
- Lepus, (Hare,) Hase.
- Ara, (Altar,) Altar.
- Eridanus, (The Po,) Fluss Eridanus.
To these forty-eight constellations of the ancients, there have been added in modern times the following fifty-eight:—
The Fifty-Eight Constellations discovered in modern times in the Northern and Southern Heavens
- Antinous, (Antinous,) Antinous.
- Coma Berenicis, (Berenice’s Hair,) Haupthaar der Berenice,
- Robur Carolinum, (Charles’s Oak,) Karlseiche.
- Columba, (The Dove,) Taube.
- Crux, (Cross,) Kreuz.
- Scutum Sobieskianum, (Sobieski’s Shield.) Sobieski’s Schild.
- Monoceros, (Unicorn,) Einhorn.
- Camelopardalis, (Giraffe,) Giraffe.
- Sextans, (Sextant,) Uranischer Sextant.
- Canes Venatici, (Greyhounds,) Jagdhunde.
- Leo Minor, (Little Lion,) Kleiner Lowe.
- Lynx, (Lynx,) Luchs.
- Vulpes et Anser, (Fox and Goose,) Fuchs und Gans.
- Lacerta, (Lizard,) Sterneidechse.
- Triangulum, (Little Triangle,) Kleines Dreieck.
- Musca, (Fly,) Fliege.
- Cerberus, (Cerberus,) Cerberus.
- Anser Americanus, (American Goose,) Amerikanische Gans.
- Phœnix, (Phœnix,) Phönix.
- Hydrus, (Hydra,) Kleine Wasserschlange.
- Dorado, (Swordfish,) Schwertfisch.
- Piscis Volans, (Flying Fish,) Fliegender Fisch.
- Chameleo, (Chameleon,) Chamaleon.
- Avis Indica, (Bird of Paradise,) Paradiesvogel.
- Triangulum, (Southern Triangle,) Südliches Dreieck.
- Pavo, (Peacock,) Pfau.
- Indus, (Indian,) Indianer.
- Grus, (Crane,) Kranich.
- Mons Msenalus, (Mount Maenalus,) Berg Mänalus.
- Cor Carolinum, (Charles’s Heart,) Herz Karl’s II.
- Cervus, (Reindeer,) Rennthier.
- Pica Indica, (Indian Bird,) Indianischer Vogel.
- Taurus Poniatowski, (Poniatowski’s Bull,) Stier Poniatowski’s
- Quadra, Square, Mauerquadrat.
- Officinum Sculptorum, (Sculptor’s Workshop,) Bildhauerwerkstatt.
- Fornax Chemica, (Chemical Furnace,) Chemischer Of en.
- Horologium, (Clock,) Pendeluhr.
- Reticulus Rhomboidalis (Rhomboidal Net,) Rhomboidisches Netz.
- Coelum Sculptorium, (Graver,) Grabstichel.
- Equuleus Pictoris, (Painter’s Easel,) Maler staff elei.
- Pyxis Nautica, (Mariner's Compass,) Seecompass.
- Machina pneumatica, (Air Pump,) Luftpumpe.
- Octans, (Octant,) Seeoctant.
- Watchman Erntehüter.
- Sceptre of Brandenburg Brandenburgisches Scepter.
- Honors of Frederick Friedrichsehre.
- George’s Harp Georgsharfe.
- Herschel’s Telescope Herschel’s Teleskop.
- Balloon Lufiballon.
- Printing Press Buchdruckerwerkstatt.
- Electric Machine Electrisir Maschine.
- Log Line Log Leine.
- Compasses Zirkel.
- Ruler and Square Lineal und Winkelmaass.
- Telescope Astronom. Fernrohr.
- Microscope Mikroskop.
- Table Mountain Tafelberg.
There are consequently 106 constellations in the heavens, forty-eight old, and fifty-eight new.
Maps of the Stars; Planisphers; Application of the Method of Alignments in Learning the Stars and Constellations
14. For the sake of more readily learning the constellations and their particular stars, as also for the more certain guidance of astronomers, those delineations on paper of the starry heavens known as celestial maps, or maps of the stars, have been invented. These maps comprehend either the two planispheres, as in pls. 12 and 13, and are then called planispheres, or they contain single parts of the heavens, and then together form an atlas. The celestial maps of Bayer, Doppelmayer, Goldbach, Flamsteed, Bode. Harding, Schwinck, Riedig, Argelander, and others, are well known. Besides the introduction of constellations, the ancients, particularly the Arabians, ascribed particular names to the brighter fixed stars, as, for instance, in Orion (pl. 12), Bellatrix and Betelgeux, Capella in Auriga, Altair in Aquila, Arcturus in Bootes. Castor and Pollux in Gemini, Marcab in Pegasus, &c., and in pl. 13, Rigel in Orion, Fomalhaut in Piscis Australis, Sirius in Canis Major, Antares in Scorpio, &c. Johann Bayer, however, in the beginning of the seventeenth century, introduced a much better and more complete assistant to the memory in recollecting and referring to the stars, by employing the letters of the Greek and Roman alphabets, which convenient notation has since been justly retained. It may be observed in the two charts of the stars, pls. 12, 13.
A very easy means of finding and readily learning the most important stars and constellations is afforded by what is called the method of alignments; this consists in having straight lines drawn in the chart (pls. 12, 13) connecting the single brighter stars, thus forming triangles and quadrilaterals, which are again reconstructed in the sky by imaginary lines drawn between these stars. This will be referred to hereafter.
The Double Stars; Remarkable Constellations of Stars; Nebulous Spots and Stars
15. By double stars is meant two stars, generally so near together that to the naked eye they appear but as a single star. There are nevertheless many double stars only visible through the telescope. These may consist of two kinds—optical, or apparent, and physical, or actual double stars. The first are such as, not related to each other, happen to fall nearly on the same line of vision; the latter are those which, connected in one system, revolve the one about the other. One of these is frequently larger than the other, although sometimes their size is nearly equal. Their colors, however, are always different. The single fixed stars and the optical double stars shine only with a whitish light, verging sometimes on yellow, sometimes on red. The physical or actual double stars, of which alone we here treat, have only been studied within the last few decades. The peculiar motions of these remarkable stars appear to occur according to the Newtonian laws of gravitation, and Savary, Encke, John Herschel, and Mädler, have already determined the orbits of many double stars, as 70 p, Ophiuchus, polar star, γ Andromedas, ζ Ursse Majoris, ζ Herculis, &c., as also their periods of revolution, which latter in some double stars amount to a few years, in others to many centuries. Since one of two double stars, as before stated, revolves around the other, it may readily happen that with respect to our earth one may pass before the other so as to cover it completely. This has actually been confirmed by observation. Thus, for instance, stars which once were double are now single, and others which were once single are now seen as double. Consequently the apparent distances of the double stars cannot be otherwise than variable. Struve has published a catalogue of 3112 double and multiple stars, arranged in order, which is thus far the most complete and accurate.
Since the double stars generally present very slight points of light of various distance and distinctness, their observation may serve as the surest test of the excellence of a telescope. Achromatic telescopes, which, for instance, merely exhibit ζ, Ursa Major, or Mizar (pl. 12, fig. 3), and γ Andromeda, Alamak (fig. 6), as double stars, are only of ordinary power. Those, however, are much better which show as double stars Castor and Pollux, or α Gemini (pl. 12, fig. 1) and the pole star, or α Ursa; Minor is (fig. 9), as also Mesarthim, or γ Arietis (fig. 8), and Cor Caroli in Canes Venatici (fig. 10). An instrument that shall show γ Virginis (fig. 2), α Arietis (fig. 5), β Ononis, or Rigel (fig. 7), and Ras Algithi, or α Herculis (fig. 4), as double, is one of extraordinary excellence. The double star Vega, or α Lyræ (fig. 11), is probably not really but only optically double, the smaller of the 12 magnitudes being distant about 43 seconds from the principal stars.
16. Among the spots of the northern heavens richest in stars belong the groups figured on pl. 12; the Pleiades, or the seven stars, fig. 12, in the back of Taurus, the Hyades, or rain stars, fig. 13, in the forehead of Taurus, the little group of stars (fig. 14) between the tips, β and ζ, of the horns of Taurus; the rich region about Vega and Lyra; the so called Lucida Lyræ; the numerous stars about Arcturus (fig. 16), in Bootes, and the vicinity of the great remarkable nebula (fig. 17) in Orion.
With respect to the nebulous spots and stars, pl. 13 (figs. 1 to 20) represents twenty of the largest and most beautiful. Fig. 1 is a double nebula in Gemini (108° 45′ right ascension, and 29° 49′ declination), consisting of two round nebulæ touching each other, which shine almost like stars. Fig. 2 exhibits the double nebula in Coma Berenicis (right ascension 187° 0′, declination 12° 8′), of great brilliancy. Fig. 3 gives a view of a small double nebula of right ascension 158° 15′, declination south 17° 55′. Fig. 4 is a curiously shaped nebula in Ophiuchus (Serpentarius). Fig. 5 represents two nebulous spots touching each other nearly at right angles, of tolerably elliptical shape, to be found in the constellation of Canes Venatici. Fig. 6 represents the remarkable annular nebula in Lyra, rt. asc. 281°; 45′, N. dec. 32° 49′, whose opening is filled with a second ash-grey nebula the whole appearing like a veil drawn over an almost circular hoop. At 33° 0′ of right ascension and 41° 34′ North declination, in Perseus, is seen a distinct and very eccentric nebula (fig. 7) of 4′ length and 40″ breadth, in whose midst is a concentric, also elliptical, space, at whose two extremes two little stars are seen. Still more remarkable is the nebulous spot (rt. asc. 268° 0′, S. dec. 23° 1′) in Sagittarius (fig. 8), seemingly split into three pieces; a double star is seen in the midst of the dark interspace. Fig. 9 gives a view of the extremely remarkable and tolerably large nebula in constellation Robur Caroli of the southern hemisphere, consequently not visible in the northern. A number of minute stars will be observed to shine out from it.
The following may be particularly mentioned among the number of irresolvable planetary nebulae. The well known great nebula in Andromeda (pl. 13, fig. 10), visible to the naked eye, of peculiar feebly glimmering light, 30′ in diameter; the stars standing in its vicinity do not appear to belong to it. A nebula (fig. 11) occurs in Cetus, similar to the one in Perseus (fig. 7), only longer and broader. A curiously shaped elongated nebula (fig. 12) is met with in Cygnus, while planetary, entirely round, and brilliant nebulous spots exhibit themselves in Sagittarius (fig. 13) and the hand of Andromeda (fig. 14). A spot (fig. 15) similar to these last is shown in Orion, and a granular nebula, with a very bright spot, in Ursa Major (rt. asc. 127° 45′, N. dec. 50° 49′). But the most remarkable, perhaps, of all is the great nebula in Orion (fig. 17), under the middle of the (so called) Jacob’s Staff, near the star Θ; distinguished above all the others by its peculiar shape (not unlike the opened jaws of a wild beast), by the curious variety in the distribution of its light, as well as by its great extent. Even the fixed stars in and about it are remarkable for their lustre, and the positions of some of them appear to have a particular relation to the nebula itself. It has been supposed, from a comparison of older figures of this nebula with its present appearance, that it has undergone a decided change, although this is by no means absolutely certain. An almost equally remarkable object is found in the constellation Vulpes (rt. asc. 298° 0′ and N. decl. 22° 17′), in the shape of a large oval nebulous spot (fig. 18), whose major axis is to its minor as 4 to 3. In the two foci are found two circular nebulae, much darker, and equally illuminated in all parts. Fig. 19 represents a curious nebulous figure found in the head of the northern Canis Venaticus. It is a round, bright, central spot, surrounded by a nebulous ring split on one side. Further improvements in the telescope will probably exhibit more clearly the true character of these wonderful objects. The Magellanic Clouds, observed in the southern hemisphere and invisible to us (fig. 20), are in like manner highly remarkable appearances of the starry heavens, consisting of isolated clear spots, like separated portions of the Milky Way. According to Horner, who has communicated some observations on these Magellanic Clouds, the greater of them is about as bright as the Milky Way in its brightest part, as near Cygnus, while La Caille was not able to find a single star in them with his 14-foot telescope.
Multiple, Variable, and New Stars
17. In conclusion, it remains to state that, besides the double stars, there are threefold and fourfold, or multiple stars, as also changeable and new stars. Threefold stars are found, for example, in Orion, under 72\(\frac{1}{2}\)° rt. asc, and 14\(\frac{1}{4}\)° N. decl., in ζ Cancer, ξ Libra, 7 Taurus, Ψ Cassiopeia, π Monoceros, Ψ Libra, as also in Lynx, under 97\(\frac{1}{2}\)° rt. asc. and 59\(\frac{3}{5}\)° N. declination. Of the fourfold stars Θ Orion is perhaps the most distinguished; it stands very near the darkest part of the great nebula in Orion; ε Lyra is also a fourfold star. Among multiple stars, ζ Orion is known as the most remarkable; it was known by Schröter as a 12-fold, but by Struve as a 16-fold star. The variable stars are also remarkable, that is, those stars whose apparent magnitude does not remain the same. These stars shine within a certain period with various degrees of brilliancy, and it is said that they have a certain period, as, for instance, Algol in Perseus, α Hercules, β Lyra, γ Antinous, δ Cepheus, &c. Nevertheless the periods of several variable stars appear subject to many irregularities. Other stars often vanish entirely, and reappear at a later period, as Mira in Cetus, κ Cygni, and seven stars in Leo, Virgo, Hydra, Corona, and Aquarius.
In addition to all these, stars have sometimes appeared suddenly in regions of the heavens tolerably free from stars, which could not have been there before; such appeared in Aquila in 389, between Cepheus and Cassiopeia in 945, again near the same place in 1264, in Cassiopeia (Tycho’s star) in 1572 and 1573, in Ophiuchus, 1604 and 1605, and in Cygnus (Anthelm’s star), 1670. Astronomers have not yet been able to frame a satisfactory hypothesis to explain the phenomena which the variable and new stars exhibit in so remarkable a manner.
![]() Theoretical Astronomy
Theoretical Astronomy
The Circle and the Ellipse
18. In the study of Astronomy a knowledge of the circle and ellipse is absolutely necessary. If a straight line, CD (pl. 6, fig. 3), make a complete revolution in the same plane around one extremity, C, the other end, D, will describe the circumference, DHAGFD, in which each point is equally distant from the centre, C. The plane surface inclosed by this circumference is called the circle. Every straight line drawn from the centre, C, to the circumference is a radius; and every straight line connecting two points of a circumference and passing through the centre is a diameter (AB). All radii are equal to each other, so also are all diameters. Any straight line connecting two points of the circumference, not passing through the centre, is called a chord (EF). It divides the circle into two unequal parts, EAHDBF and EGF, of which the latter, as the smaller, is called the segment. The diameter, AB, on the contrary, divides the circle into two equal parts, AHDB and AEGFB, called semicircles. The angle. DCB, formed by two radii, DC and CB, at the centre of the circle, is called a central angle; the surface, BCD, inclosed between a central angle and the arc of the circumference inclosed between the radii, is called a sector. Finally, a straight line outside of the circle and touching the circumference in only one point, is called a tangent, JK.
An ellipse, ADBEA (pl. 6, fig. 4), is a complete curve, possessing the peculiarity that, if two straight lines be drawn from certain points, SS′, in its area, called the foci, to any point in the circumference, their sum will be equal to the sum of similar lines drawn to any other points. Thus SP + S′P = Sp + S′p. This same sum will also be always equal to the length of the greater axis, AB. The lines SP and S′P (or also Sp and S′p) are called the radii vectores of the point P (or p). The straight line, DC, passing through the centre, C, at right angles to the major axis, AB, is called the minor axis. CS or CS′ is called the eccentricity of the ellipse. Should this ellipse represent the orbit of a planet in one of whose foci the sun is situated, then if the planet be situated at P or p, the line SP or Sp will be the radius vector of the planet.
Parallax; Horizontal Parallax and Parallax in Altitude; Parallax of a Place
19. Fig. 5 will serve for the explanation of what astronomers mean by the word parallax. Let ABD represent the meridian circle of a place of observation, A; C the centre of the earth; let H J be a part of the infinitely distant sphere of the heavens; finally, let the moon be at M. The line HCD represents the true horizon, aAa′ the apparent horizon of the place, A. If the moon be supposed to stand in the horizon at M, it will be referred by an observer at A to that part of the celestial sphere occupied by the star a. From the centre of the earth it would be referred in the direction CM to the celestial sphere at b. The angle AMC, or aMb, will represent the difference of the two directions; and this angle, AMC, is called the parallax of the point M, or its horizontal parallax, since M is situated in the horizon. Let the moon now stand higher in the heavens, as at M′, then from A she will be seen in the direction AM′c, consequently referred to the point c of the heavens; and from C, the centre of the earth, in the direction CM′d, referred consequently to the celestial sphere at d. The angle CM′A = cM′d will be the difference of the two directions CM′ and AM′; and CM′A will be the parallax of M ', more definitely its parallax in altitude, because M′ is situated a certain distance above the horizon. Let the moon now be situated at M″, or in the direction of the zenith, e, of A, then the moon, M″, will be referred to the heavens at e; the two lines of sight will coincide, and they will form no angle, so that for heavenly bodies situated in the direction of the zenith, the parallax in altitude vanishes or becomes zero. We find, also, by examining the figure that the parallax is at its maximum in the horizon, diminishing with the angle of elevation until in the zenith it is zero.
Suppose now a second place of observation, E, lying in the same meridian, and the moon to be situated at M′; then from A she will be seen in the direction AM′c, consequently referred to c, and from E in the direction EM′d′, and referred to d′. The angle EM′A gives the difference of the two directions EM′. AM′. This angle EM′A, or the corresponding arc cd′, is called the local parallax of the star at M′ for the two places A and E. Hence it is clear, that for the same altitude of the same star, its local parallax will be less as the distance of the two places of observation on the same meridian is less.
The Heliocentric and Geocentric place of the Planets; their Commutation and Annual Parallax
20. The motions exhibited by the planets are not so simple as the apparent daily motions of the fixed stars, as above considered. This results from the fact of their having two motions, of which one is diurnal, in common with the fixed stars, from east to west, and the other an orbitual motion from west to east. Add to this, that the planets are not, like the fixed stars, almost infinitely distant from us, and that therefore it makes a material difference whether their revolutions be observed from the sun or the earth. The place of a planet, as seen from the sun, is called its heliocentric place; its position as seen from the earth, is the geocentric place. Fig. 14, pl. 6, is intended to illustrate these terms. Let S be the centre of the sun, the circle described through T the orbit of the earth, that through P the orbit of any superior planet, and the extreme circle, the ecliptic; the exterior and interior circles lying, of course, in the same plane, which may be the plane of the paper. Furthermore, let the earth be at T, the planet at P, and let ♈︎ be the vernal equinox. The arrows give the direction of the motions of the earth and planet, as also the order of the signs of the ecliptic. The planet P will now be seen from the sun, S, in the direction Sp; the angle ♈︎Sp, or the arc ♈︎p, will consequently be the heliocentric longitude of the planet, and the angle ♈︎ST, or the arc ♈︎t, the heliocentric longitude, of the earth. From the earth T, the planet P will evidently be seen in the direction Tp′. It is further allowable, on account of the almost infinite distance of the fixed stars, to consider the line TA parallel to S♈︎ as meeting in the same point of the celestial sphere, and consequently A and ♈︎ as coinciding. The angle ATp′ then, or the arc ♈︎p′, is the geocentric longitude of the planet; and since the plane of the planet at P has a certain inclination to the common plane of the inner and outer circles, the angle PSQ, or the arc PQ, will represent the heliocentric latitude of the planet, if the arc PQ be supposed drawn from the planet P, perpendicular to the plane of the earth’s orbit. Finally, the angle PTQ will be the geocentric latitude of the planet. The angle PTS, at the earth, will be the elongation of the planet, or its apparent angular distance from the sun, this elongation being (pl. 6, fig. 14) equal to the heliocentric longitude of the earth, + 180°, diminished by the geocentric longitude of the planet. From the preceding it follows that p will be the heliocentric, and p′ the geocentric place of the planet, with respect to the ecliptic. We can speak in the same manner of the heliocentric and geocentric position of a planet with respect to the equator, and consequently of the heliocentric and geocentric right ascension and declination.
We have still to speak of the commutation and the annual parallax of a planet. The commutation is the angle PST (fig. 14), at the sun, S, obtained by deducting the heliocentric longitude of the earth from the heliocentric longitude of the planet. The annual parallax is the angle TPS, at the planet P, obtained by deducting the heliocentric longitude of the planet from its geocentric longitude. It is very evident that we can never speak of the geocentric place of the earth.
Some other Important Elements in the Theory of the Planetary Motions
21. The mean anomaly, the true anomaly, the perihelion distance, and the aphelion distance, are far more important to the theory of the planetary motions than the commutation and the annual parallax. If, for instance, m (fig. 15) be the mean place of a planet, p the true place, then rays, Sm, Sp, from the sun to these two positions will form, with respect to the major axis AP, of the elliptical planetary orbit, the angles mSP′, pSP, which are respectively called the mean and the true anomaly of the planet. Their great importance consists in this, that the mean anomaly expresses the uniform or the mean motion in the circle, while the true anomaly expresses the true motion in the ellipse. The true anomaly, or the angle PSp, consists of two parts, angles mSP′ and mSp. This latter angle, mSp. however, which evidently is the difference between the true and mean motions of the planet, is called the equation of the orbit, and is one of the most essential elements in the theory of the planetary motions. For, knowing the equation of the orbit, the sum of the mean anomaly and the equation of the orbit gives the true anomaly, and consequently the true—that is, the elliptic longitude of a planet in its orbit. In conclusion, P is the perihelion and A the aphelion of the planet, in which points it will be respectively at its least and greatest distances from the sun.
Eclipses of the Sun and Moon
22. We come now to eclipses of the sun and moon (pl. 6, fig. 18). The full moon at times loses gradually its light in a manner just as if a blackish grey disk were drawn slowly over its face, moving from left to right, and passing off on the opposite side. An eclipse of the moon is then said to take place, which, as it only occurs when the moon is full, and, indeed, when the full moon is in or near the straight line connecting the centres of the sun and earth, is of easy explanation. The earth, as an opake globe illuminated by the sun, must throw a shadow into space on the side opposite to the sun, this shadow being conical, and longer than the distance of the moon from the earth. The moon must also, as a body likewise illuminated by the sun, lose partly or entirely her light by passing partly or entirely into the shadow of the earth. If the moon’s orbit lay in the plane of the ecliptic, it is clear that an eclipse would occur at every full moon, which experience shows not to be the case. We learn above, section 8, that the path of the moon is inclined 5° 8′ 48″ to the ecliptic; the full moon passes for the most part, therefore, above or below the earth’s shadow, and it is only when the full moon happens in or near one of the moon’s nodes, that the moon can encounter the earth’s shadow. As the moon’s nodes do not remain in the same part of the ecliptic, it is very evident that the eclipses of the moon (and sun) must take place in different years and months, so that definite periods arise, after whose lapse the eclipses again occur in the same months.
Astronomy teaches the conditions necessary for the occurrence of an eclipse. Should the full moon be situated at a distance from one of its nodes of less than 12\(\frac{1}{2}\)°, the moon may be partially eclipsed. Should the distance be less than 9\(\frac{1}{2}\)°, and greater than 5\(\frac{1}{2}\)°, a partial eclipse must take place. The eclipse will be total, that is, the moon will be entirely obscured, when the full moon takes place at less than 5\(\frac{1}{2}\)° from one of the nodes. A merely partial eclipse of the moon cannot last more than 2 hours and 18 minutes; the time of a partial, and at the same time total eclipse, may amount to 4 hours and 24 minutes. Astronomers are accustomed to determine beforehand the particular circumstances of an eclipse of the moon, as the beginning, the middle, and the end of the obscuration, the countries in which it will be visible, as well as the size of the eclipsed portion. The latter is given in digits (1 digit = \(\frac{1}{12}\) of the diameter of the disk). Unfortunately, however, the period of beginning and ending of an eclipse cannot be exactly determined, as the earth’s shadow falling on the moon (pl. 6, fig. 18), like any other shadow, is not bounded by sharp outlines, but fades off into light, and in every eclipse there is also distinguished a full shadow or umbra, and a half shadow or penumbra. From the preceding it is clear that an eclipse of the moon is not merely an apparent, but a real occurrence. Consequently, the inhabitants of all those portions of the earth in which the moon shines at the time of the eclipse, see every particular of the eclipse in the same manner and at the same time, even if the local times of the places should be different.
Sometimes a black disk is seen to pass gradually from right to left before the sun. But as this phenomenon is not seen alike at all places above whose horizon the sun may be at the time, since in some countries the sun is covered more or less than in others, or not at all, it is evident that this phenomenon cannot be the result of an actual obscuration of the sun. It is rather produced by the moon (pl. 6, fig. 18, and pl. 14, fig. 56), since it only happens at the time of new moon. It has been observed that these uncommon phenomena, called eclipses of the sun, occur only when the new moon happens to be in or near one of its nodes. By its intervention between the earth and sun, it then hides the view of the latter entirely or partly from the former. The phenomenon exhibited, is precisely as if the sun in a cloudless sky were covered for a time by a little black cloud passing over his disk. As the shadow of the cloud moves along in the plain beneath, in the direction in which the cloud is driven by the wind, and conceals from the observer whom it overtakes the sight of the sun, while others out of the bounds of the shadow still see that luminary; just so the shadow of the moon moves along over the earth’s surface from west to east in the direction of the moon’s motion around the earth, conceals from the countries traversed by it the view of the sun, and produces the phenomenon of eclipse. All regions not thus traversed see the sun as usual.
Eclipses of the sun are distinguished into partial, total, central, and annular. An eclipse is partial, when the moon covers the sun only in part; total, when this covering is complete. When the moon’s disk is apparently smaller than that of the sun and stands directly before him, the eclipse is annular. A total or annular eclipse is central when the centres of the sun and moon’s disk coincide. For the entire earth’s surface, a partial eclipse can last about 7 hours; one, partial and total, 4 hours and 48 minutes; but for a given place on the earth’s surface, a total eclipse cannot continue more than 4\(\frac{1}{2}\) hours at the very utmost. The calculation of the separate circumstances of an eclipse of the sun becomes, therefore, more difficult and circumstantial than those of the moon, since, as before mentioned, the former are not actual occurrences like the latter, but only apparent phenomena, whose shape, size, and duration depend upon the place of the observer on the earth’s surface.
An eclipse of the sun cannot take place when the new moon is more than 1° 35′ distant north or south of the ecliptic: 1° 24′ is the minimum distance that the moon can pass near the sun without causing an eclipse. A north or south latitude of the moon less than 1° 24′ at time of new moon always produces an eclipse of the sun, whose extent, as in the case of the lunar eclipses, is given in digits (12 digits = diameter of the sun’s disk). Hence it follows that the limits of possible occurrence of eclipses are much more extended in the case of the sun than in that of the moon. Consequently it follows that, for the whole surface of the earth, the former are much more frequent than the latter, for on an average there may happen within 18 years 41 eclipses of the sun and only about 29 of the moon. At least two eclipses of the sun must occur annually, because the sun every six months comes in the neighborhood of the moon’s ascending or descending node; while eclipses of the moon may be wanting for an entire year. But for any particular place on the surface of the earth, as, for instance, Leipzig, the visible eclipses of the moon are thrice as numerous as those of the sun. It may be assumed that every part of the earth’s surface may expect a partial eclipse of the sun within every two years, and a total within 200. Sometimes, though but rarely, the number of solar and lunar eclipses for the entire earth may amount to seven in a year, occurring then in January, July, and December.
By the actual observation of a solar eclipse, its beginning and end can be determined much more accurately than the same circumstances of a lunar eclipse. For this reason observations on the former are much more certain assistants in determining geographical longitude.
The course and extent of the moon’s shadow over the surface of the earth during a total or annular eclipse of the sun is shown by fig. 56, pl. 14. It represents also the manner in which the principal circumstances of such a phenomenon are usually delineated on a map.
The Planetary Systems of Ptolemy, Copernicus, Tycho, and the Egyptians. Tabular Exhibition of the Most Important Features of our Planetary System.
23. By a planetary system, the ancients understood the disposition and course of seven planets with respect to our earth. Since the time of Copernicus, however, by the solar system, in the ordinary acceptance of the term, is meant the disposition and mutual arrangement of 14 primary and 19 secondary planets about our sun, which system is commonly termed the Copernican. By a solar system, taken generally, is understood any fixed star of the heavens, as a sun, with the spheres revolving about it as planets. Since astronomy has been pursued as a science, four planetary systems have had the greatest share of attention, being, in order of time, that of Ptolemy, the Egyptians, Copernicus, and Tycho.
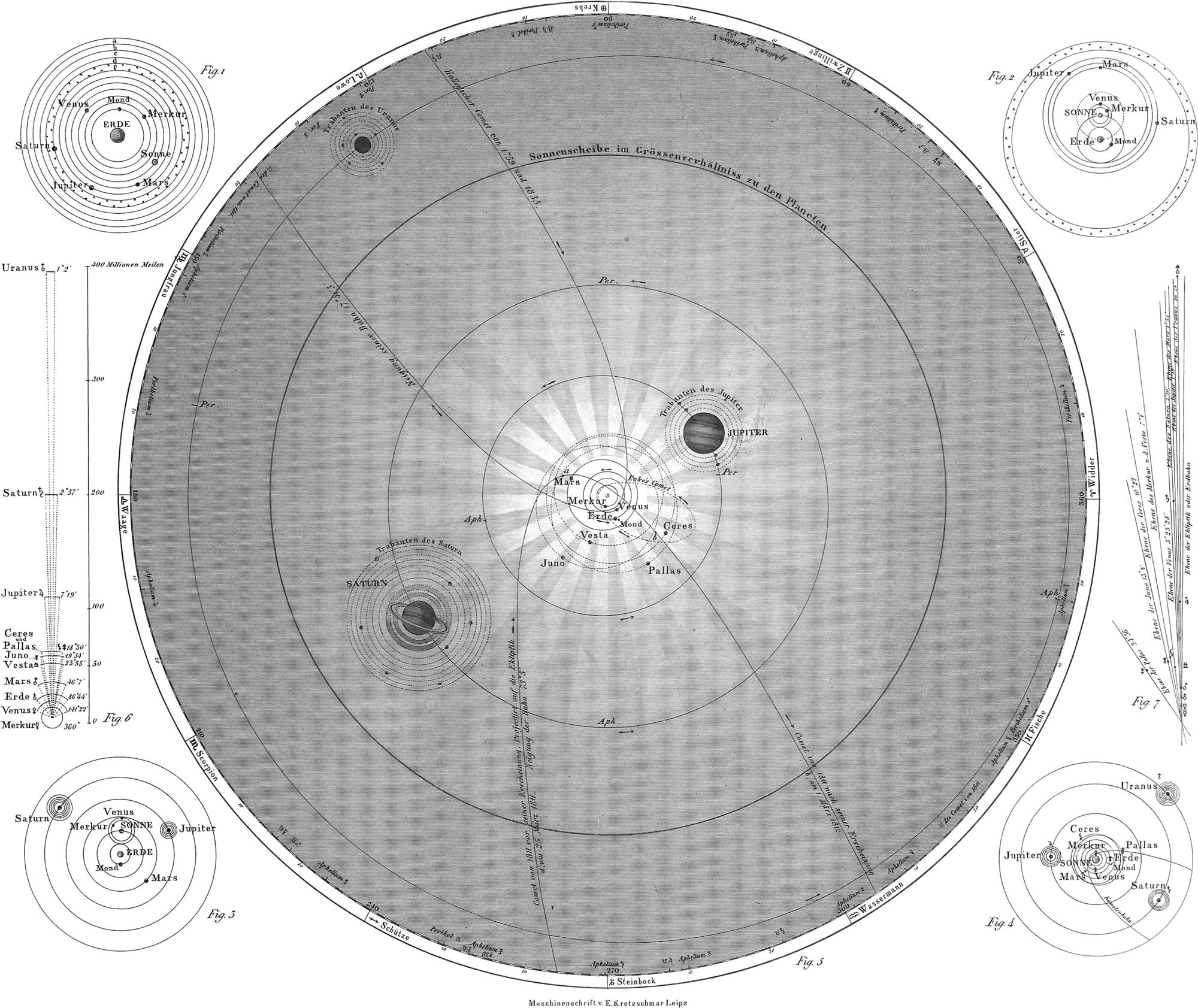
According to Ptolemy (an astronomer of Alexandria, living about a.d. 150), the earth (pl. 7, fig. 1) stands immovably in the centre of 12 circles. From the earth outwards the seven first circles represent the paths of the following bodies as planets, and in the following order:—the Moon; Mercury; Venus; the Sun; Mars; Jupiter; and Saturn. The eighth circle, e, represents the path of the fixed stars; the ninth, d, and tenth, c, called the first and second crystal heavens, were intended to serve in explaining the phenomena produced by precession (precession of the equinoxes); the eleventh circle, b, called primum mobile, was supposed to carry along the ten circles inclosed by it, in its daily rotation from east to west, while each planet traverses its ascribed path from west to east about the earth; the twelfth and last circle, a, Ptolemy indicated by the name of Empyrseum, or the abode of spirits and the blessed. This Ptolemaic system explains the heavenly appearances only imperfectly, provides in no way for the varying distances of the planets, and is, on the whole, very unnatural; it endured, however, with little change until the time of Copernicus.
Certain of the Egyptian astronomers easily perceived that the arrangement of the orbits of Venus and Mercury, according to Ptolemy, could not be the true one, since it could not explain the superior conjunctions of these two planets. They, therefore, allowed the moon, and then the sun, to revolve (pl. 7, fig. 2) round the earth, but supposed Venus and Mercury to revolve round the sun in minor orbits, accompanying it in its revolution round the earth. Mars, Jupiter, and Saturn moved in great circles about the earth, as in the Ptolemaic system. This system, termed the Egyptian, is as false as the Ptolemaic, and could not be maintained so long in authority. It was reserved for the great Copernicus (1472–1543) to teach the world the true theory of the arrangement of the primary and secondary planets, afterwards confirmed by the laws of Kepler, and the discovery by Newton of the law of universal gravitation. According to this theory the sun ☉ is a fixed star, occupying the centre of as many circular orbits as there are primary planets. These latter occur in the following order from the sun; Mercury ☿, Venus ♀, Earth ♁, Mars ♂, Jupiter ♃, Saturn ♄; the Moon ☽︎, a secondary planet, revolves about the earth, and with it around the sun. All these motions take place in the direction from west to east (shown by the direction of the arrows, fig. 5).
Tycho de Brahe, who lived in the second half of the sixteenth century, certainly recognised the correctness of the Copernican system at an early period, but his ambitious vanity, and perhaps still more his religious prejudices, urged him to oppose it. In Tycho’s opinion the earth could not move around the sun, because the Bible would be thereby falsified. He preferred to represent the earth (fig. 3), like the earlier theorists, as placed immovably in the centre of the universe, the moon revolving round it first, and then the sun; around which latter the other planets, Mercury, Venus, Mars, Jupiter, and Saturn, revolve as their centre. This system of Tycho, however, could not longer maintain any stand when the true Copernican system had been discovered. The Copernican system received a very essential confirmation by Kepler, who showed that the planets revolve in orbits that are ellipses, but which differ very little from circles, the sun being situated in one focus common to all (pl. 10, fig. 2). This is also approximately exhibited in pl. 7, fig. 5, by the eccentric position of the circular planetary orbits.
Since the invention of the telescope, the following primary and secondary planets have been discovered as members of our solar system; the four moons of Jupiter, the ring and seven satellites of Saturn, the planet Uranus ♅ (March 13, 1781, by Herschel), his six moons also by Herschel, Ceres (Jan. 1, 1801, by Piazzi), Pallas (March 28, 1802, by Olbers), Juno (Sept. 1, 1804, by Harding), Vesta (also by Olbers, March 29, 1807), Astræa (Dec. 8, 1845, by Henke), Neptune ♆, his ring and moon (Sept. 23, 1846, by Galle), and the planet provisionally called Iris (July 1, 1847, by Henke). The orbits of all these planets and moons, except Astræa, Iris, and Neptune, are represented on pl. 7, fig. 5, upon which are represented also the orbits of Halley’s Comet 1759, 1835, and of the great comet of 1811, as well as that of Encke. The outer circle of the figure represents the ecliptic with its division into the 12 signs, and on it are indicated by corresponding signs, in what parts to look for the following points:—the ascending node, ☊, of the great comet of 1811; the aphelion of Mars; the aphelion of Jupiter; the descending node, ☋, of Mars; the aphelion of Juno; the perihelion of Vesta; the descending nodes of Mars and Venus; the aphelion of Saturn; the descending node of Jupiter; the aphelion of the Earth; the descending node of Saturn; the aphelion of Pallas and Venus; the descending node of the Comet of 1811, and the aphelion of Ceres. In addition to these are given the proportional diameters for the Sun, Jupiter, Saturn, and Uranus.
24. Since the planets move slower in their orbits as their distance from the sun is greater, fig. 6, pl. 7, is intended to exhibit the relative velocity of these motions. When Mercury, the planet nearest to the sun, has completed an entire revolution in 360°, Venus in the same time describes an arc of 141° 22′, the Earth an arc of 86° 44′, &c. The proportionate velocities of the recently discovered planet Astraea (between Vesta and Juno) and Neptune (almost twice the distance of Uranus from the sun) could not well be represented in the figure. Astræa, if introduced into the preceding comparison, would describe an arc of about 21°, and Neptune one of about 20′. From the measurement of these various axes, it results, that Venus moves 2\(\frac{1}{2}\), the Earth 4, Mars 8 times slower than Mercury. Fig. 7 represents the inclinations of all the planetary orbits (except those of Astræa, Iris, and Neptune) to the plane of the ecliptic or the earth’s orbit.
25. We shall now present a tabular view of the most important elements of our planetary system, principally with regard to those points which could not be represented on pl. 7, without affecting the distinctness of the figures. The estimates are given in English geographical miles, according to the most recent observations and calculations. The different values ascribed to Neptune may possibly require rectification whenever his elements are better known than they can be now.
| Planets | Mean distance from the Sun | Eccentricity | Sidereal period in mean solar days and Julian years | |||||
|---|---|---|---|---|---|---|---|---|
| Mercury | 32,000,000 | 6,580,000 | 87d | 23h | 15′ | 36″ | ||
| Venus | 65,392,000 | 412,000 | 224d | 16h | 49′ | 7″ | ||
| Earth | 82,664,000 | 1,388,000 | 365d | 5h | 9′ | 10″ | 7‴ | |
| Mars | 125,956,000 | 11,740,000 | 1y | 321d | 17h | 30′ | 41″ | |
| Vesta | 195,212,000 | 17,296,000 | 3y | 229d | 17h | 38′ | 0″ | |
| Astræa | 212,64,000 | 18,706,000 | 4y | 49d | 6h | 8′ | 50″ | |
| Juno | 220,672,000 | 56,400,000 | 4y | 132d | 1h | 36′ | 0″ | |
| Ceres | 229,052,000 | 17,564,000 | 4y | 223d | 17h | 38′ | 0″ | |
| Pallas | 229,192,000 | 55,468,000 | 4y | 225d | 7h | 19′ | 0″ | |
| Jupiter | 430,084,000 | 20,732,000 | 11y | 314d | 20h | 2′ | 7″ | |
| Saturn | 788,516,000 | 44,232,000 | 29y | 166d | 23h | 16′ | 32″ | |
| Uranus | 1,185,692,000 | 73,892,000 | 84y | 5′d | 19h | 41′ | 36″ | |
| Neptune | 2,900,584,000 | 25,524,000 | 167\(\frac{1}{2}\) | |||||
| Planets | Mass The Sun = 1 |
Density Earth = 1 |
Gravitation Earth = 1 |
Light & Warmth Earth = 1 |
Rotation in Mean Solar Time | ||
|---|---|---|---|---|---|---|---|
| Mercury | 1.2025810 | 2.94 | 1.15 | 6.67 | 1d | 0h | 5′ |
| Venus | 1.401847 | 0.92 | 0.91 | 1.91 | 0d | 23h | 21′ |
| Earth | 1.354936 | 1.00 | 1.00 | 1.00 | 0d | 23h | 56.1′ |
| Mars | 1.2680337 | 0.96 | 0.50 | 0.43 | 1d | 0h | 37.3′ |
| Jupiter | 1.1054 | 0.24 | 2.69 | 0.037 | 0d | 9h | 55.5′ |
| Saturn | 1.3500 | 0.14 | 1.26 | 0.011 | 0d | 10h | 29.3′ |
| Uranus | 1.17918 | 0.24 | 1.05 | 0.003 | |||
| Planets | Surfaces in Square Miles | Volumes in Thousands of Cubic Miles |
|---|---|---|
| Mercury | 22,272,000 | 10,210,816 |
| Venus | 144,048,000 | 163,373,248 |
| Earth | 148,512,000 | 170,180,672 |
| Mars | 40,096,000 | 23,825,280 |
| Vesta | 148,500 | 832 |
| Juno | 4,448,000 | 850,880 |
| Ceres | 5,936,000 | 1,361,472 |
| Jupiter | 18,710,496,000 | 230,635,198,720 |
| Saturn | 12,088,880,000 | 124,082,652,800 |
| Uranus | 2,802,416,000 | 13,954,799,360 |
| Sun | 1,865,312,000,000 | 239,460,953,480,000 |
| Moon | 10,350,400 | 3,024,812 |
| Planets | Mean Velocity in a Second | Fall towards the Sun in a Second | Right Ascension of the Eternal Node of the Orbit |
|---|---|---|---|
| Mercury | 26.8 Eng miles | 8.46 | 316° 51′ |
| Venus | 19.6 Eng miles | 2.42 | 242° 45′ |
| Earth | 16.4 Eng miles | 1.27 | 248° 0′ |
| Mars | 13.6 Eng miles | 0.55 | 254° 21′ |
| Vesta | 10.8 Eng miles | 0.20 | 180° 33′ |
| Juno | 10.4 Eng miles | 0.20 | 197° 3′ |
| Ceres | 10.0 Eng miles | 0.20 | 208° 43′ |
| Pallas | 10.0 Eng miles | 0.20 | 182° 19′ |
| Jupiter | 6.8 Eng miles | 0.047 | 242° 5′ |
| Saturn | 5.2 Eng miles | 0.014 | 231° 12′ |
| Uranus | 4.0 Eng miles | 0.003 | 247° 30′ |
| Neptune | 2.8 Eng miles |
| Planets | Inclination of the Orbit to the Sun’s Equator | Arc of the Retrograde Motion | Duration of the Retrograde Motion | ||
|---|---|---|---|---|---|
| Mercury | 2° 54′ | 8° 33′ | 16° 18′ | 20 and 24 days | |
| Venus | 4° 9′ | 15° 20′ | 16° 31′ | 41 and 43 days | |
| Earth | 7° 30′ | ||||
| Mars | 5° 50′ | 11° 8′ | 19° 30′ | 62 and 81 days | |
| Vesta | 4° 28′ | ||||
| Juno | 16° 28′ | ||||
| Ceres | 3° 43′ | ||||
| Pallas | 37° 8′ | ||||
| Jupiter | 6° 24′ | 10° 0′ | 119 days | ||
| Saturn | 5° 57′ | 6° 48′ | 137 days | ||
| Uranus | 6° 44′ | 3° 36′ | 151 days | ||
The most important items respecting the moons of Jupiter, Saturn, and Uranus, will be found further on, principally in section 33. Sections 30 and 31 will contain the principal points in the history of our moon.

26. The central figure on pl. 8 is intended to exhibit clearly, with many other phenomena, the annual revolution of the earth about the sun; nevertheless, for the better knowledge of the whole subject, it will be necessary to premise a few general observations. It is. in the first place, evident that bodies cannot themselves change their condition, and that thus a body once set in motion can never stop—that it will continue to move in the same direction and with the same velocity as when it set out, unless some other external force changes its direction or velocity. This peculiarity of bodies is called inertia. It is, moreover, evident, by reference to what is said, sec. 46, of the parallelogram of forces, that if the paths of the planets, and consequently of the earth, also be ellipses about the sun, two forces must combine to their production. The one is the attractive force of the sun, varying with the distances; the other a continuous tangential force, originating in an impulse. Pl. 10, fig. 2, will show how an elliptical orbit for each planet is produced by the co-operation of these two forces. We have to remark, finally, that gravitation communicates to all freely falling bodies a tendency towards the centre of the earth.
We will now direct our attention to the orbit of the earth, with the help of the figure in pl. 8, representing its motions. By measuring the distances of the earth from the sun, at different times of the year, the shape of its orbit has been ascertained. These distances, as they were unequal, could not, of course, be semi-diameters of a circle, but they corresponded, taken together, to the radii vectores of an ellipse (pl. 10, fig. 2). The mean distance of the earth from the sun, is about 95,103,000 (statute) miles; it moves in its orbit at the average rate of 16\(\frac{4}{10}\) (Eng. geog.) miles in a second; the eccentricity of its orbit amounts to 0,016,784; the least or perihelion distance from the sun, to 81,276,000 (Eng. geog.) miles, or 33,917,997 hours; while the greatest or aphelion distance is 84,052,000 (Eng. geog.) miles, or 35,085,379 hours. The straight line connecting the perihelion and aphelion, passing through the centre of the sun, is called the line of apsides. The inclination of the earth’s orbit to its equator, or the so-called obliquity of the ecliptic, amounts to 23° 27′. The velocity of the earth is greatest at the perihelion and least at the aphelion. It is further to be observed, that the mean distance of the earth from the sun is equal to half the major axis of the earth’s orbit, and the line of apsides is itself the major axis. There are four noteworthy points in the earth’s orbit; they are those which mark the beginning of the four seasons. Two of these points are called the solstices—they mark the beginning of winter and summer. The straight line (pl. 8) uniting them, passing through the centre of the sun, is called the solstitial colure. The two other points are the equinoxes, vernal and autumnal, marking the commencement of spring and autumn. The straight line connecting these points, passing through the centre of the sun, is the equinoctial colure. It still remains to observe, that the axis of the earth being always parallel to the axis of the heavens, may also be conceived to coincide with it; for, in consequence of the great distance of the fixed stars from our sun, the diameter of the earth’s orbit (of more than 190,000,000 [statute] miles), as well as the whole orbit itself, would be seen as a mere point at the stars.
The representation on pl. 8, shows the position of the earth on the first day of each of the twelve months of the year, the solar distances corresponding to these twelve positions, and the shape of the earth’s orbit. The horizontal projection has been chosen, in order to represent to the eye the increase and diminution of days, and the variation of illumination about the pole of the earth. The deeper circle surrounding the pole at a short distance, is intended to represent the parallel of latitude of Paris, or the hour circle of that place divided into twenty-four hours. Although at the end of December the earth is nearest the sun, yet at that time in the northern hemisphere, the heat is less than at any other. The reason of this lies in the fact of the short days and long nights, as well as that the sun’s rays fall very obliquely on the earth, traversing a longer path through the atmosphere, and consequently losing much of their heating power. At the beginning of July, on the contrary, although then the earth is at its greatest distance, the temperature of the northern hemisphere is greatest, on account of the long days and short nights, and the great altitude of the sun at noon. This, of course, depends upon the declination of the sun north or south from the equator. This declination of the sun for the first day of every month, is given in pl. 8. The great inner circle contains the division of the year into days and months, and enables us, by drawing a straight line to any point of this circle, to find the situation of the earth on the day corresponding to the point. The external circle, on the contrary, is divided into twelve equal arcs, of which each one answers to a sign (30 degrees) of the ecliptic. It must not be forgotten, however, that owing to the precession of the equinoxes, these signs no longer correspond to the constellations of the same name, so that now the sign Pisces corresponds to the constellation Aries, the sign Aries to the constellation Taurus, &c. It is further evident from an inspection of the plate, that if the earth at the beginning of spring, summer, autumn, and winter, should be in the signs Aries, Cancer, Libra, and Capricornus respectively, then the sun, as being always directly opposite in the ecliptic, will be in the signs Libra, Capricornus, Aries, and Cancer.
By properly combining the preceding with sections 27, 28, which are devoted principally to an explanation of the theory of the seasons, and particularly of the daily and yearly motion of the sun, it will not be difficult to obtain a perfect idea of all the phenomena occurring in the course of a year, over the whole surface of the earth. On account of the great importance of this subject, it may be remarked further, that the changes of days and nights, as also of the seasons, may be very easily represented by means of a Tellurium, or by means of a terrestrial globe, with a little simple additional mechanism.
The inner space of pl. 8, is employed to represent the orbits of the two inferior planets, Mercury and Venus, in their proportional size, shape, and eccentricity. The accompanying figures are readily intelligible without further explanation.
27. The sun is stationary! It is incredible that so enormous a body as the sun should have three different motions at the same time. Accurate observations have shown that the earth moves about its axis from west to east, once every day, by means of which the daily apparent motion of the heavens, as well as of the sun, from east to west is produced. It is further- more only apparently, not really, that the sun in the course of a year moves around the earth from west to east in an ellipse termed the ecliptic (pl. 9, fig. 3, LCD), making an angle with the equator of 23° 27′. This inclination, termed the obliquity of the ecliptic, combined with the revolution of the earth, explains the apparent motion of the sun. both towards the north and towards the south. If, for instance, we suppose the sun on June 21st to have reached the point L, it is evident that while the earth rotates about her axis, ax, from west to east, or in the direction from Q to U, it will seem as if the sun in the same time, but from east to west, had described the parallel circle, VOLV (or the tropic of Cancer), about the earth; where the sun is at R, he will appear to describe the equator CRFC; and on December 21st, the tropic of Capricorn or the circle DHMD. The planes of the equator and tropics intersect the earth in circles, which are respectively the terrestrial equator and the terrestrial tropics. It is further to be observed that the poles, N, K, of the ecliptic, during the apparent daily rotation of the heavens, describe two small circles, of which the northern, AN, is called the arctic, the southern, BK, the antarctic. The polar circles of the earth corresponding to these are u, y, and k, b.
The rotation of the earth on its axis, and the inclination of the ecliptic to the equator, explain without any difficulty the inequality of days and nights, and the succession of the seasons. For when the sun on the 21st June traverses the tropic of Cancer, he remains much longer above the horizon zz than when describing the tropic of Capricorn on Dec. 21. In this latter case we readily perceive that the sun remains much longer below the horizon, and that consequently the nights are much longer than on the 21st of June. It is further evident, that about the 20th of March and 23d of September, when the sun is on the equator, an equality of days and nights must take place. Figs. 1 and 3, pl. 9, also show that during the six months that the sun is north of the equator, spring and summer must take place in the northern hemisphere, autumn and winter in the southern; but during the six months that this luminary is south of the equator the case must be reversed, spring and summer now happening in the southern hemisphere, autumn and winter in the northern.
28. All that has hitherto been said with regard to phenomena occurring in connexion with the earth, can only be explained by the assumption of a rotatory motion of the earth about an axis at the same time with a revolution about the sun in an elliptical orbit (pl. 9, fig. 1). The inequality of the seasons is a necessary consequence of the elliptic motion of the earth, and of the inclination of its axis of rotation to the plane of the ecliptic. If, for instance, the axis of rotation were perpendicular to the plane of the ecliptic, then there would be no change of seasons, but rather a single continuous torrid, temperate, or frigid zone. In this case also the planes of the equator and ecliptic would coincide, and as the sun would remain constantly in this plane, the days and nights would be equal the whole year through, and the poles of the earth be illuminated by only half the sun’s disk. The equatorial regions would have a burning summer continually, the temperate zones would have an eternal spring, and the polar lands would experience without intermission intense cold, in which ice would never melt. But the axis of the earth, ever parallel to itself, is inclined to the plane of the ecliptic 66° 33′, and thence follows,—1st, a progressive difference in the length of the days and nights for all points of the earth’s surface from the equator to the poles, and from the first day of the year to the last; 2dly, an increase and diminution of temperature for the northern and southern hemispheres, in proportion as these are turned more or less to the sun. Pl. 9, fig. 1, shows that the earth (revolving in the direction of the arrows), wherever in her orbit she may happen to be, always has her axis constantly parallel to itself and at the same angle of inclination to the plane of her orbit. The earth is found at A, on Dec. 21, in the beginning of winter, the shortest day of the year for our northern hemisphere. The sun is then at his greatest distance south, describes the tropic of Capricorn, and at noon stands in the zenith to all inhabitants of the earth whose latitude is 23° 27′ south. The north pole, nevertheless, lies in the middle of its six months’ night. The boundary of the earth’s shadow will fall in the north polar circle, whose inhabitants will then have a night of 24 hours. On the other hand, this will be summer to the southern hemisphere, and its inhabitants will have the longest days. This point, A (fig. 1), of the earth’s orbit is the winter solstice; the earth, which now, seen from the sun, stands in 0° of Cancer, will traverse the part AB of its orbit in 89 days, from Dec. 21 to March 20, thus marking the duration of the winter.
B is the position of the earth on the first day of spring (autumn for the southern hemisphere): the sun then describes the equator (see the direction of the equinoctial line), and as the shaded portion of the earth divides the parallel circles into two equal parts, the days and nights will at this time be equal all over the world. At the north pole the long day of six months is just commencing. The earth, standing in 0° of Libra, now traverses the part BC of its path in 93 days, from March 20th to June 21, marking the duration of spring.
C is the position of the earth on June 21, the first day of summer (of winter in the southern hemisphere); the sun then describes the tropic of Cancer, and the north pole lies in the middle of its day of six months. The inhabitants of the north polar, or arctic circle, see the sun for 24 hours, and all other dwellers oh the northern hemisphere have longer days than nights. The south pole lies in the middle of its night of six months, and the inhabitants of the southern hemisphere have longer nights than days. C is the summer solstice, and the summer lasts 94 days, that is, the time from June 21st to Sept. 23, during which the earth passes from C to D. The earth itself, on the 21st June, as seen from the sun, stands in 0° of Capricornus.
Finally, on the 23d Sept., the first day of autumn (spring for the southern hemisphere), the earth is at D, the sun standing again in the equator, the days and nights are again equal all over the earth. The sun now becomes invisible to the north pole, and visible to the south pole, the autumnal equinox occurring on Sept. 23d, the vernal on March 20. Autumn lasts 89 days, that is, the interval from Sept. 23d to Dec. 21, in which time the earth traverses the distance DA of its orbit.
From the preceding explanation it is evident that the four seasons are not of equal duration, for spring and summer together embrace 187 days, while autumn and winter last only for 178 days. There is thus a difference of nine days between the times occupied by the earth in traversing BC, CD, and DA, AB. This difference of nine days is a consequence partly of the eccentricity of the earth’s orbit, partly of the varying velocity with which the earth moves around the sun.
The Transit of Mercury and Venus across the Disk of the Sun
29. When the inferior planets, Mercury and Venus, during their revolution around the sun, come into inferior conjunction, and at the same time into or not far from the imaginary straight line drawn through the centres of the sun and earth, they will, if examined through a telescope, be seen as dark spots passing over the sun’s disk (pl. 14, fig. 55). These transits of Mercury and Venus belong to the rarer celestial phenomena, since they evidently can only take place when inferior conjunction occurs near one of the nodes of their orbits. It is plain that with regard to the origin and progress of these transits, the conditions are precisely the same as in eclipses of the sun, which latter might be called with equal propriety, transits of the moon over the sun’s disk. Astronomy teaches that Venus at her inferior conjunction must be within 1° 49′ of one of her nodes, and Mercury within 3° 28′, for a transit to occur to any observer on the earth’s surface. These two limits, then, determine the periods of these occurrences, which for Venus are 8 and 113\(\frac{1}{2}\) years, and for Mercury 6, 7, 10, and 13 years. Thus, transits of Venus happened on June 5, 1761, and June 3, 1769; the next will take place December 9, 1874, and December 6, 1882, June 7, 2004, and June 5, 2012. Pl. 9, fig. 6, exhibits the 13 transits of Mercury during the present century, with its direction each time over the sun’s disk. It is to be remembered that Mercury as well as Venus will enter on the left (eastern) limb of the sun, and emerge on the right (western) limb, for the reason that at the time of their inferior conjunction these planets are retrograding. The reason of the transits of Venus occurring in the beginning of June and December, and those of Mercury only at the beginning of May and November, lies in the fact, that at these times the earth is in the line of nodes of each planet respectively. On account of the small apparent diameters of Venus and Mercury, these phenomena could not be detected before the discovery of the telescope. The first transit of Mercury was observed by Gassendi at Paris, November 7, 1631; the first transit of Venus by Horrox, at Hoole, in England, December, 1639.
The observation of the transit of Venus is to the astronomer of vast importance, as it is almost the only certain way of obtaining the sun’s parallax, and hence of finding the mean distance of the sun from the earth, Halley first recognised this fact, and recommended these transits to the observations of astronomers. His suggestion was followed out when the next transits occurred in 1761 and 1769, and at these times observations were made in many places. The transit of 1769 was observed in the South Seas, in California, as also in the northern regions of Asia. Venus at the time of her inferior conjunction is very near the earth, and consequently seen from different places on the earth’s surface, will be referred to very different points on the sun’s disk, so that first of all the parallax of both Venus and the sun can be obtained. According to Encke, who has fully and most accurately carried out the calculation, the mean horizontal parallax of the sun at the equator amounts to 8\(\frac{5776}{10,000}\) seconds, and consequently the mean distance of the earth from the sun to 95,103,000 (English) miles. That the transits of Mercury are not available in determining the sun’s parallax, is readily intelligible, when we know that the parallax of Mercury at its inferior conjunction is not very different from that of the sun, while the parallax of Venus at inferior conjunction is almost four times as great as that of the sun.
Pl. 9, figs. 7 and 8, represents the individual phenomena of the transits of Mercury for the whole earth, as they occurred May 4, 1786. The obscure portions in figs. 7 and 8 cover those regions in which the transit was visible, the bright portions answer to the countries in which it was invisible. Those places lying in the boundary of the obscure and light parts, observed, as indicated in the figures, either an entrance or emersion at sunrise only, or an entrance or emersion at sunset only.
Additional Remarks on the Course of the Moon

Glossary for plate 10
- Abend, Evening; — stern, Evening star.
- Abnehmender Mond, Decreasing moon.
- Aphelium, Aphelion.
- Apsidenlinie, Line of Apsides.
- Aufsteigender Knoten, Ascending node.
- Austritt beim A.ufgang der Sonne, Emersion at sunrise;—beim Untergang der Sonne, Emersion at sunset.
- Axe der Ekliptik, Axis of the Ecliptic.
- Bahn des Merkur, Orbit of Mercury;—der Venus, Orbit of Venus.
- Colur des Frühlings-Æquinoxiums, Colure of the vernal equinox;—des Herbst-Æquinoxiums, Col. of the Autumnal equinox;—der Nachtgleichen, Col. of the equinoxes;—des Sommersolstitiums, Col. of the Summer solstice;—des Winter solstitiums, Col. of the Winter solstice.
- Comet von 1811 vor seiner Erscheinung. Projectirt auf die Ekliptik am 25 März 1811. Neigung der Bahn 75° 5′, Comet of 1811 before its appearance. Projected on the ecliptic March 25, 1811, Inclination of the orbit 75° 5′.—von 1811 nach seiner Erscheinung b. am 1 März 1812, Comet of 1811 after its appearance until March 1, 1812.
- Dauer der längsten Nachte, Duration of the longest nights;—des langsten Tages, Duration of the longest day.
- Dichteres Medium, Denser medium.
- Drei Uhr Morgens, 3 o’clock A. M.;—Nachmittag, 3 o’clock P. M.
- Dritter Octant, Third octant.
- Dunneres Medium, Rarer medium.
- Ebene der Pallas, d. Juno, &c., Planes of the orbits of Pallas, Juno, &c.
- Eintritt beim Aufgang der Sonne, Entrance at sunrise;—beim Untergang d. Sonne, Entrance at sunset.
- Ekliptik, Ecliptic.
- Erdaxe, Axis of the earth.
- Erdbahn, Orbit of the earth.
- Erde, Earth.
- Erster Octant, First octant.
- Erstes Viertel, First quarter.
- Excentricität, Eccentricity.
- Frühling, Spring.
- Frühlingsnachtgleiche, Vernal equinox.
- Gemässigie Zone, Temperate zone.
- Grosse Axe, Axis of the heavens.
- Halley’scher Comet v. 1759 u. 1835, Neigung seiner Bahn, Halley’s Comet of 1759 and 1835, inclination of its orbit.
- Heisse Zone, Torrid zone.
- Herbst, Autumn.
- Herbstnachtgleiche, Autumnal equinox.
- Horizont, Horizon.
- Kalte Zone, Frigid zone.
- Kometenbahn, Orbit of a comet.
- Letztes Viertel, Last quarter.
- Millionen Meilen. Millions of miles.
- Mittag, Noon.
- Mittelkraft, Mean force.
- Mitternacht, Midnight.
- Monate, Months.
- Mond, Moon;— -bahn, Orbit of the moon;—-finsterniss, Eclipse of the moon.
- Morgen, Morning;—-stern, Morning star.
- Neumond, New moon.
- Neun Uhr Abends, 9 P.M.;—Morgens, 9 A.M.
- Niedersteigender Knoten, Descending node.
- Nord, North;—-pol, Northpole.
- Nördliche Declination der Sonne, Northern declination of the sun.
- Nördlicher Polarkreis, Arctic circle.
- Obere Conjunction, Superior conjunction.
- Œstliche Digression, East digression.
- Ost, East.
- Perihelium, Perihelion.
- Polarstern, Polar star.
- Polhöhe über dem Horizont, Elevation of the pole above the horizon.
- Richtung des Schattens um Mittag, Direction of the shadow at noon.
- Roiationsaxe, Axis of rotation.
- Scheinbarer Himmelsbogen, Apparent arch of the heavens;—Horizont, visible horizon.
- Sechs Uhr Abends, 6 P.M.;—Morgens, 6 A.M.
- Solstitial oder Wendepunktlinie, Solstitial colure.
- Sommer, Summer;—-Sonnenwende, Summer Solstice.
- Sonne, Sun;—Sonnen-Æquator, Sun’s equator;—-finsterniss, Eclipse of the sun;—-scheibe im Grössenverhaltniss zu den Planeten, The sun’s disk; its size compared to the diameters of the planets.
- Stunden, Hours;—Entfernung, Hours’ distance;—-ring, Hour-circle.
- Süd, South;—-pol, South pole.
- Südliche Declination der Sonne, Southern declination of the sun.
- Südlicher Polarkreis, Antarctic circle.
- Südwestlicher Sonnenrand, Southwestern edge of the sun.
- Trabanten des Jupiter;—des Saturn;—des Uranus, Satellites of Jupiter, Saturn, and Uranus.
- Untere Conjunction, inferior conjunction.
- Vierter Octant, Fourth octant.
- Vollmond, Full moon.
- Vom Pol bis zum Zenith, From pole to zenith;—Zenith biz zum Æquator, From zenith to equator.
- Wahrer Horizont, True horizon.
- Wendekreis des Krebses, Tropic of Cancer;—des Steinbocks, Tropic of Capricorn.
- Westliche Digression, West digression.
- Winter- Sonnenwende, Winter solstice.
- Zoll, Digit, inch.
- Zunehmender Mond, Increasing moon.
- Zweites Octant, Second octant.
30. We have already said all that is essential with respect to the origin of the moon’s phases, the inclination of the moon’s orbit to the ecliptic, the retrograde motion of the moon’s nodes, as also the causes of solar and lunar eclipses. There still remain a few additional considerations respecting the moon’s course. The principal figure on pl. 10, fig. 5, contains the phases of the moon, or the various aspects under which she presents herself to us. The earth being in the centre of the external circle, the moon’s orbit is so placed, with reference to this circle, as readily to exhibit its eccentricity. The moon revolves in this orbit from west to east around the earth, and the figure represents her in her proper proportion to the earth and in the eight principal points of her course. The sun may be supposed to be stationed at a distance to the right of the earth in pl. 10, exceeding 410 times that of the moon from the earth. In order to exhibit the phases of the moon in their fullest conditions, they are represented within the moon’s orbit in much larger proportion. The orbit of the moon is properly an ellipse, the earth standing in one of the foci. Its eccentricity amounts to 0.0548442; the greatest distance of the moon from the earth (that is at time of the apogee), to 63.842 semi-diameters of the earth, and the least, or that at time of perigee, to 55.916 semi-diameters. Both perigee and apogee retrograde from evening to morning about 40° 42′ annually. The moon appears to revolve in 24 hours from east to west around the earth, which, with the apparent daily motion of the heavens, is produced by the rotation of the earth on her axis. Again, the moon, as full moon during the nights of summer, appears to describe a very small arc, and during the nights of winter a very large arc above the horizon, which is explained in the following manner: Let us suppose the night to be that of the winter solstice (pl. 9, fig. 1), on December 21, consequently the longest night in the year. Let now the earth (pl. 10, fig. 4) be opposite the sun, situated in the tropic of Capricorn, which it describes on this day, and the moon, as full moon at M, in the tropic of Cancer, which she describes; our horizon, HR, shows that the diurnal arc of the sun is very small, while the moon traverses by night a very large arc. The contrary of this must take place on the night of the summer solstice, June 21, the shortest night of the year. Should the moon, as full moon in spring and autumn, stand in the equinoxes as the sun, she would then be as long above as below the horizon.
31. If we suppose the moon to be at L′ (pl. 10, fig. 3), in conjunction or between the earth and sun, then the centres of these three bodies will be in the straight line RE. While the moon is completing a revolution around the earth, moving daily about 13° 10′ 35″, the earth will have passed forward over a certain part of her orbit, about to t. The moon will then be at n, in a direction, xz, which is parallel to the former, RE. The moon has consequently a periodical or tropical revolution completed within 27 days, 7 hours, 43 minutes, 4\(\frac{7}{10}\) seconds. For the moon to return to conjunction, however, that is, again to become new moon, it must in addition traverse the arc nh, equal to the arc Tt or Rm, described by the earth in its orbit, which arc amounts to about 27°. To accomplish this the moon requires somewhat more than two days; she consequently returns to conjunction in 29 days, 12 hours, 14 minutes, and 3 seconds. This period is known as the lunar month (in its proper sense), and the revolution itself (from conjunction to conjunction) is the synodic revolution, or simply the lunation, which may also be counted from one full moon to another. Pl. 10, fig. 10, shows that the course of the moon projected on the plane of the earth’s orbit, must form a kind of serpentine. The moon has yet to pass over the arc nv (fig. 3), to come back to the. same fixed star; this return, accomplished in 27 days, 7 hours, 43 minutes, and 12 seconds, is called the sidereal revolution of the moon. Finally, the revolution of the moon, with respect to the nodes of its orbit, occupies 27 days. 5 hours, 5 minutes, and 36 seconds.
The moon revolving about our earth is forced to accompany her in her course round the sun, so that the path traversed by the moon in space is properly an epicycloid. This compound motion of the moon is, consequently, the source of the various phases represented in fig. 5, as already explained in sections 7 and 29. Pl. 10, fig. 5, shows, in addition, the first, second, third, and fourth octants, as also that the moon, when full, is in opposition to, and when new, in conjunction with the sun. The inclination of the moon’s orbit to the earth’s equator is very variable, ranging in 19 years from 18° 19′ to 28° 36′. The inclination of the moon’s equator to the ecliptic (1° 28′ 25″) never varies. The time of the rotation of the moon about her axis corresponds precisely with that of her mean revolution around the earth, consequently equal to 27 days, 7 hours, 43 minutes, and 12 seconds. Hence the moon always turns the same side to us, and the opposite side is constantly concealed, except the small part of it revealed by libration. For this reason the conclusion was early formed, though too hastily, that the moon had no rotation.
The Primary Causes of the Elliptical Orbits of the Planets; Kepler’s Laws
32. In the explanation of the yearly course of the earth about the sun (by means of the figure on pl. 8), it was mentioned that the paths of the planets, and consequently those of the earth and moon, are ellipses, which are produced by the co-operation of two special forces. How that takes place will be explained hereafter. Let us suppose that any body (as ♏︎, pl. 10, fig. 2) once set in motion is impelled by two forces; let the line ♏︎P represent the direction and intensity of the one force, the line ♏︎V the direction and intensity of the other. It is evident that the body ♏︎ will not move towards S, the sun alone, nor towards x alone. It must rather (see what is said, section 26, about compound motion) follow the direction ♏︎o, and pass to the point ♐︎; the force represented by ♏︎P is the attractive force of the sun at S, and the force represented by ♏︎V, is the tangential force produced by an impulse. As the ever-varying central force, namely the attraction of the sun, is constantly acting upon this tangential force, this must also vary. The curvature ♏︎♎︎, ♏︎♌︎, of a planet’s orbit, produced by the co-operation of these two forces in the first, and in all following moments, must manifestly depend upon their relative proportion. The central force again depends upon the distance of the planet from the sun. Should the original velocity of the planet in the first second be exactly equal to the planet’s fall towards the sun in the same second, then the ratio will be 1:1, and the orbit will be a circle. It is perfectly plain, however, and much more probable, that the original velocity may have been a little greater or less than what would be necessary to the production of a circular orbit. Then the planet would move in an ellipse (pl. 10, fig. 2), in which the point z, where the planet started, would be the perihelion if the projectile force had been the greatest, for it would recede from the sun from the very beginning of its motion. But if the planet had started in the point ♋︎, the projectile force must have been the lesser of the two, and the point ♋︎ would be the aphelion. The higher mechanics shows that ellipses arise when, beginning at the perihelion, the original velocity amounts to from 51\(\frac{96}{100}\) to 73\(\frac{36}{100}\) English geographical miles in a second, and that ellipses likewise arise when, beginning in the aphelion, the original velocity amounts to from \(\frac{4}{100}\) to 51\(\frac{88}{100}\) geographical miles in a second. It has actually been found that the planets (and their moons), whether starting in their perihelion or aphelion, must have had initial velocities falling within the above limits, and consequently must describe elliptic orbits.
If the tangential force operate on the point ♏︎, in the direction V♏︎, and the attractive force of the sun in the direction P♏︎, the point m will move in the direction ♏︎♎︎ to ♎︎. At ♎︎ the tangential force operates in the direction B♎︎, and the central force in the direction p♎︎, therefore the point ♎︎ now moves in the direction ♎︎♍︎ to ♍︎. At ♍︎ the tangential force acts afresh in the direction D♍︎, and the central force in the direction k♍︎, consequently the point ♍︎ now moves in the direction ♍︎♌︎ to ♌︎, &c. It is hence evident that the planet must describe an ellipse, not, however, the broken line ♏︎♎︎, ♍︎♌︎. For we may suppose the parallelogram of forces to be constructed anew every successive moment, and consequently infinitely small, so that instead of the broken line, a continually curved one, namely an ellipse, will be produced, since both forces, the central and tangential, operate incessantly upon the planet. It is only for the more intelligible illustration of the subject that the single parallelograms in fig. 2 are represented on so large a scale; the eccentricity, CS, is, for the same reason, assumed tolerably great, as the real eccentricity of the planetary orbits is much less.
The proposition that the planets describe ellipses, the centre of the sun being in one of their foci, is the first of the three celebrated laws of Kepler, upon which the whole theory of the planetary motions depends. The second law (discovered, however, first) is, that any two areas (sectors), SQq and SQ′q′, described by the radii vectores, SQ and Sq, SQ′ and Sq′, are proportional to the times (pl. 6, fig. 4). This law may also be expressed in this manner: The different velocities of a planet are as the squares of its different distances from the sun. Suppose the planet to describe the distances Qq, and Q′q′ of its orbit in equal times, then the elliptical sectors, SQq and SQ′q′, will have equivalent areas. Hence it follows, that if the areas of the sectors at the perihelion B and at the aphelion A are to be equivalent, the arc described by the planet at the perihelion must be greater than that described in equal time at the aphelion. Thus the planet must move with the greatest velocity at the perihelion, and the least at the aphelion, and these two different velocities are as the squares of the distances SA and SB. In general, the velocity of a planet’s motion must be greater as it approaches the sun, and less as it recedes from it.
The first law of Kepler expresses the character of the curve described by the planets; the second, the varying velocities of the planetary motion; while the third law is a bond of union connecting the different planets together. This third law is expressed as follows: the squares of the times of revolution of two planets are as the cubes of their mean distances from the sun. The great value of this law consists in its presenting a geometrical proportion, so that knowing three of the four elements, the mean distances from the sun, and the periods of revolution, the fourth can always be obtained. In conclusion, the laws of Kepler are true laws of nature, since Newton has demonstrated that they are only consequences of that single and supreme law discovered by him—the law of universal gravitation.
The Moons of Jupiter, Saturn, and Uranus
33. The planet Jupiter is accompanied by four moons in his journey of 11\(\frac{1}{2}\) years around the sun. Immediately after the discovery of the telescope, Simon Marius (at Ansbach), in November, 1609, observed four small stars very near to Jupiter, which, almost always in a straight line with him, appeared sometimes to the right, sometimes to the left, never separating far from him. Marius observed them carefully, and in March, 1610, was convinced that those four small stars were moons of Jupiter. Galileo observed them for the first time on January 10th, 1610.
Indicating the satellites of Jupiter by I., II., III., IV., their mean distances from the centre of Jupiter are as follows:—232,000 (English) geographical miles for I.; 372,000 for II.; 592,000 for III.; and 1,040,000 for IV. The eccentricities of their orbits (pl. 10, fig. 6) are inconsiderable, as also their inclinations. The sidereal period of I. is 1 day, 18 hours, 28 minutes; of II., 3 days, 13 hours, 14 minutes; of III., 7 days, 3 hours, 43 minutes; and of IV., 16 days, 16 hours, 32 minutes. These are uncommonly short, and consequently eclipses of Jupiter’s moons occur with remarkable frequency. We often see one or another moon vanish suddenly and re-appear on the eastern side after the lapse of some hours. A tolerably attentive examination soon shows that such an eclipse of the moon is produced by the shadow of the primary. This also shows incontestably that Jupiter and his four moons are opake bodies, deriving all their light from the sun.
By the assistance of a good telescope, it will frequently be observed that these moons enter Jupiter’s disk on the eastern border, moving towards the western border, accompanied by circular dark spots, going in the same direction and with the same velocity. These spots are evidently nothing else than the shadows of the moons cast from them upon the surface of Jupiter. These phenomena are consequently eclipses of the sun to Jupiter, produced by his moons. The maximum duration of the eclipses amounts for satellite I., to 2 hours, 16 minutes; for II., to 2 hours, 52 minutes; for III., to 3 hours, 34 minutes; and for IV., to 4 hours, 45 minutes. In one year of Jupiter, that is in almost 12 of our years, 4,400 eclipses of the moons, and as many of the sun, may be observed. The beginning and ending of the same eclipse of I. and II. are never both seen, as before the opposition to Jupiter only the beginning, and after it, only the ending are observed. On the other hand, both beginning and ending in III. and IV. may be perceived. With respect to eclipses of the sun, it is to be remarked that at the time of visible beginning, the shadows follow the satellites, and precede them at the time of ending. In conclusion, one moon of Jupiter may sometimes, though rarely, eclipse another.
Observations of the so frequently occurring eclipses of Jupiter’s satellites offer an exceedingly ready means of determining geographical longitude. Unfortunately, the moment of such an eclipse, just as in the case of an eclipse of our moon, will be observed very differently at different places, owing to the unequal illumination and magnifying power of telescopes, and the different acuteness of sight of the several observers. It was the observation of the eclipses of Jupiter’s satellites that led the Danish astronomer, Olaus Homer (in the latter half of the seventeenth century), to the discovery of the velocity of light.
When Jupiter is at his mean distance from the earth, the diameters of his moons appear to us respectively at angles of 1″.02, 0″.91, 1″.49, 1″.27. Hence the apparent diameters of his moons to Jupiter will be 31′ 11″, 17′ 35″, 18′ 0″, and 8′ 54″. The true diameters are for I., 2,120; for II., 1,880; for III., 3,120; and for IV., 2,040 English geographical miles; their densities are \(\frac{1}{5}\), \(\frac{2}{5}\), \(\frac{3}{10}\), and \(\frac{1}{4}\) that of the earth.
34. The planet Saturn, on his 30 years’ journey around the sun, is accompanied by seven moons, revolving round him from west to east. Huyghens discovered one of these moons, namely, the sixth, March 25, 1655. Cassini found the seventh and most distant on October 25, 1671, the fifth on December 13, 1672; as also in March, 1684, the third and fourth. One hundred years after, August 28 and Sept. 17, 1789, Herschel discovered the two satellites nearest the planet. The orbits of the six inner moons (pl. 10, fig. 7) are nearly circular, and lie almost entirely in the plane of Saturn’s ring; the orbit of the seventh, however, lies nearly in the plane of the ecliptic. Their periods of revolution are days, 22 hours, 38 minutes; 1 day, 8 hours, 53 minutes; 1 day, 21 hours, 18 minutes; 2 days, 17 hours, 45 minutes; 4 days, 12 hours, 25 minutes; 15 days, 22 hours, 41 minutes; and 79 days, 7 hours, 55 minutes. Their mean distances from Saturn amount, in geographical miles, to 76,680, 99,640, 163,880, 211,680, 295,480, 642,840, 2,098,744. With regard to the true magnitudes, masses, and densities of the satellites of Saturn, nothing satisfactory is known, as these moons are among the smallest and most remote objects of the heavens. Schröter estimated the true diameter of the fifth and sixth satellites at 1,040 and 2,720 geographical miles. It is only since 1830 that the sixth moon has received a more accurate determination by Bessel.
The first and second moons had only been seen by their discoverer Herschel, until in 1836 Camont found the second, and in June 27, 1838, the astronomers at Rome were enabled to observe the first. The seventh or outermost moon revolves about Saturn at the great distance of 2,098,744 geographical miles, and has the remarkable peculiarity of almost entirely vanishing when to the east of Saturn, and of shining brightest in its western elongation. This is probably produced by. the fact of its completing a rotation about its axis in the time that it is accomplishing a revolution about Saturn, presenting the same side to the earth when it comes into the same position with respect to its primary—the one side reflecting the sun’s light much more completely than the other, consequently the equality of the time of rotation and revolution in the secondary planets appears to apply to these bodies also. The moons of Saturn are sometimes eclipsed, and sometimes produce eclipses of the sun to inhabitants of Saturn; nevertheless, both kinds of eclipses, which always follow closely the time of the disappearance of the ring, occur more rarely than in the case of Jupiter, a consequence of the great inclination of their orbits to that of Saturn (pl. 10, fig. 7). Yet eclipses of Saturn’s moons often occur among themselves, and are also caused by the ring.
35. Uranus, on his 84 years’ journey about the sun, is accompanied by six moons (fig. 8). Herschel, on January 11, 1787, discovered the second and fourth; on January 18, 1790, the first; on February 9, 1790, the fifth; on February 28, 1794, the sixth; and on March 26, 1794, the third satellite of Uranus. These moons are at the following successive distances from their primary, expressed in geographical miles, 196,000, 254,000, 296,000, 339,600, 680,000, and 1,360,000. Their magnitudes, so difficult to determine, must be very great to make them visible at so immense a distance from the earth. The plane of their orbits is almost perpendicular to that of the orbit of Uranus (fig. 8); and it is remarkable that these six moons have the unique motion from north to south. The inclination of the equator of Uranus to its orbit, or the obliquity of his ecliptic, is very nearly a right angle, whence all difference of zones must disappear; while, on the other hand, that of seasons must be very great. When near one pole of Uranus, the sun stands during summer almost immovably in the zenith, and afterwards, for almost a year, describes a very small circle about the zenith; in like manner, the satellites present themselves a very long time in the first and last quarters. New moon and full moon only take place when a pole of Uranus has the sun in its horizon, and at this time alone can eclipses of the sun and moons occur.
In conclusion, it may be remarked that figs. 6, 7, and 8, pl. 10, represent somewhat in perspective, the systems of the moons of Jupiter, Saturn, and Uranus; and fig. 9, the orbit of our moon. The proportional size of the orbits is represented as accurately as the small size of the scale would allow.
Estimates of the proportional size of the Planets
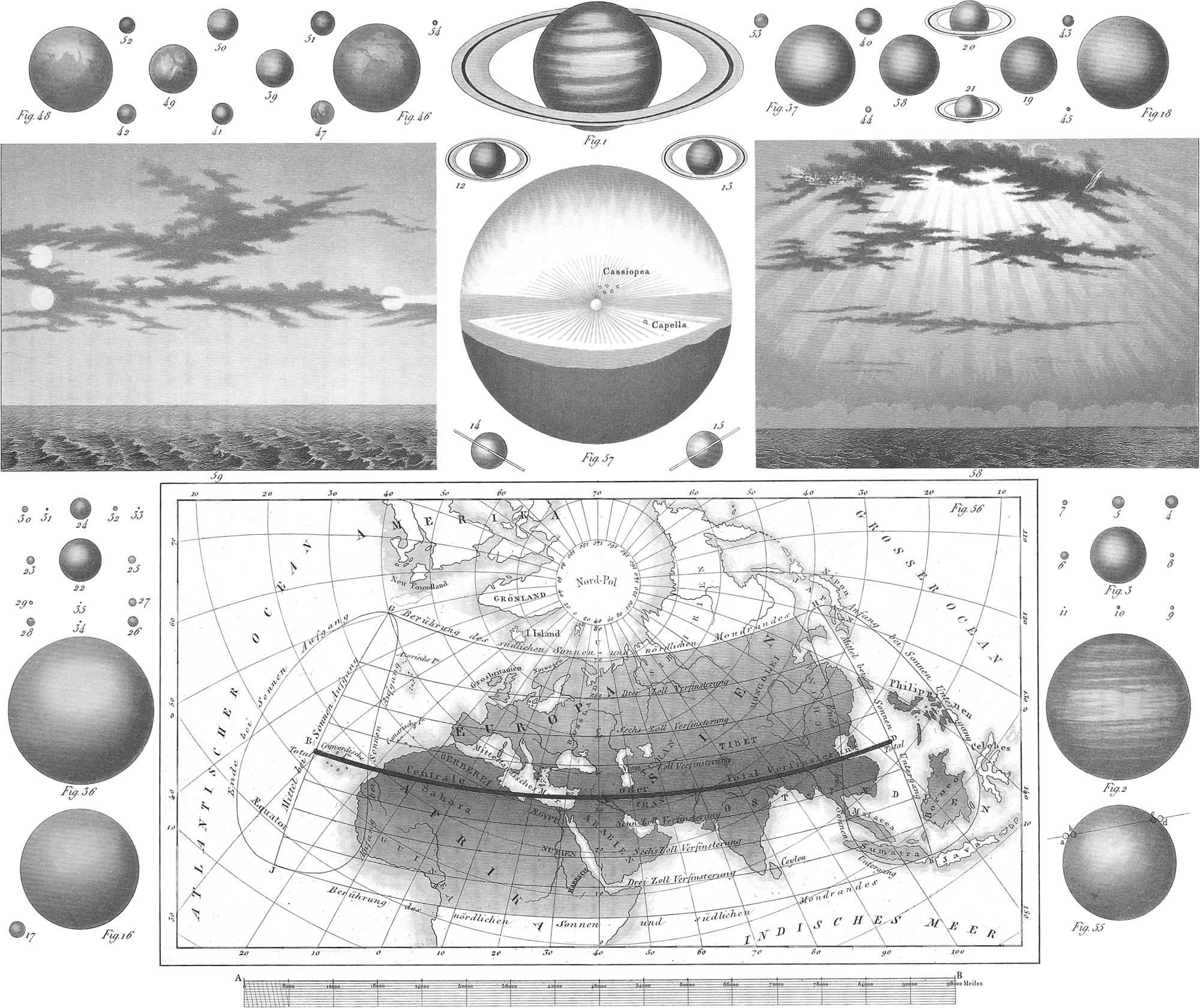
Glossary for plate 14
- Anfang bei Sonnenaufgang, Beginning at sunrise;—bei Sonnenuntergang, beginning at sunset.
- Arabien, Arabia.
- Atlantischer Ocean, Atlantic Ocean.
- Azorische Inseln, The Azores.
- Berberey, Barbary.
- Berührung des Sonnen-, und Mondrandes, Contact of the edges of sun and moon.
- Canarische Inseln, Canary Islands.
- Capverdische Inseln, Cape Verd Islands.
- Centrale oder totale Verfinsterung, Central or total eclipse.
- Diet Zoll Verfinsterung, Three digits eclipsed.
- Ende bei Sonnenaufgang, End at sunrise;—bei Sonnenuntergang, End at sunset.
- Grönland, Greenland.
- Grossbritanien, Great Britain.
- Grosser Ocean, Pacific Ocean.
- Indisches Meer, Indian Sea.
- Island, Iceland,
- Mittel bie Sonnenaufgang, Middle at sunrise;—bei Sonnenuntergang, Middle at sunset.
- Mittelländisches Meer, Mediterranean Sea.
- Mongolei, Mongolia.
- Neun Zoll Verfinsterung, Nine digits eclipsed.
- Nordpol, North pole.
- Norwegen, Norway.
- Nubien, Nubia.
- Ost Indien. East Indies.
- Russland, Russia.
- Seeks Zoll Verfinsterung, Six digits eclipsed.
- Sibirien, Siberia.
36. To obtain a clear idea of the relative size of the planets (Astræa, Neptune, and Iris excepted) and the sun, we may compare the scale at the bottom of pl. 14, representing the sun’s radius, with the diameters of the circles representing the planets (figs 1 to 11). Taking the diameter of the sun, 2AB, at 770,944 geographical miles, that of the eleven planets in geographical miles, and the ratio of the planets’ diameters to that of the sun, will be as follows:—
| Figs | Planets | True Diameter | Ratio of the Diameters of Planets to the Sun’s Diameter |
|---|---|---|---|
| 1 | Saturn | 62,072 | 1 : 12\(\frac{3}{5}\) |
| 2 | Jupiter | 77,228 | 1 : 10 |
| 3 | Uranus | 28,888 | 1 : 25\(\frac{4}{5}\) |
| 4 | Earth | 6,880 | 1 : 112\(\frac{1}{10}\) |
| 5 | Venus | 6,776 | 1 : 113\(\frac{3}{5}\) |
| 6 | Mars | 3,572 | 1 : 215\(\frac{4}{5}\) |
| 7 | Mercury | 2,688 | 1 : 286\(\frac{4}{5}\) |
| 8 | Pallas | 1,800 | 1 : 428\(\frac{3}{10}\) |
| 9 | Ceres | 1,360 | 1 : 566\(\frac{9}{10}\) |
| 10 | Juno | 1,200 | 1 : 856\(\frac{2}{5}\) |
| 11 | Vesta | 200 | 1 : 3,854\(\frac{7}{10}\) |
| Planets | Actual Volume in Millions of Geographical Miles | Ratio of True Volumes of the Planets to that of the Sun |
|---|---|---|
| Sun, | 14,966,308,588 | 1 : 1 |
| Jupiter, | 15,039,700 | 1 : 995 |
| Saturn, | 7,817,666 | 1 : 1914 |
| Uranus, | 872,175 | 1 : 17,160 |
| Earth, | 10,636\(\frac{4}{10}\) | 1 : 1,407,122 |
| Venus, | 210\(\frac{8}{10}\) | 1 : 1,465,733 |
| Mars, | 1489 | 1 : 10,052,599 |
| Mercury, | 638 | 1 : 23,458,165 |
| Pallas, | 180\(\frac{8}{10}\) | 1 : 82,778,261 |
| Ceres, | 85 | 1 : 176,489,500 |
| Juno, | 53\(\frac{2}{10}\) | 1 : 281,321,609 |
| Vesta, | \(\frac{7}{77}\) | 1 : 288,101,459,569 |
37. Pl. 14, figs. 12–15, gives the four principal positions of Saturn and his rings, with respect to our earth, as they are perceived during the 29\(\frac{1}{2}\) years’ revolution of Saturn about the sun. Fig. 12 gives a view of Saturn and his rings at the time this planet is situated in the sign of Cancer (♋︎); fig. 13 represents them when—14\(\frac{3}{4}\) years later—Saturn is found in the sign of Capricornus ♑︎; fig. 14, when in the sign of Libra ♎︎; and fig. 15, when—14\(\frac{3}{4}\) years later—he is found in Aries ♈︎.
The dimensions of the rings, as also their distances from each other and from Saturn, will be found in sec. 58. This ring system is, however, no great source of gratification to the inhabitants of Saturn, as it is only visible in the middle equatorial regions of the planet. It does not shine by night, only during the day, or a litcle while after sunset and before sunrise, and even this in general only during the summer. For at night the whole ring is shaded by Saturn; and in winter, instead of illuminating the planet, it casts a shadow upon the side of the planet opposite to the sun, covering an area of many millions of miles, and lasting in part almost fifteen of our years. On the other hand, the inhabitants of the surface of the ring will perceive Saturn’s hemisphere in their horizon, of enormous size, and should they be on the very edge of the ring, they will perceive the planet in their zenith about 20,000 times larger than the sun. The floor itself upon which they stand, reaches to the right and to the left, visible up to the heavens, closing beyond the planet, thus affording beyond all question an entirely unique and most magnificent spectacle.
38. Every planet revolving about the sun must have at one time a period of least, and at another one of greatest distance from the earth. In the first case the planet is said to be in its perigee, in the second in its apogee. The two inferior planets, Mercury and Venus, are in their perigee at inferior conjunction, and in their apogee at superior conjunction; the superior planets are in apogee at conjunction, and in perigee at opposition. On account, however, of the different eccentricities, as well as the different inclinations of the planetary orbits to that of the earth, the perigee and apogee for each planet cannot be always the same. The consequence of this is, that seen from the earth, the planets do not always appear of equal apparent size. Each planet must appear greatest in its perigee, and least in its apogee. The difference for all the planes is approximately represented in pl. 14, figs. 16–35, according to the scale AB, whose larger divisions measure 25 seconds, the smaller 2\(\frac{1}{2}\). This difference at the time of perigee is the following:—
Distance of the Planets from the Sun, and apparent Diameter at time of Greatest Perigee
| Figs | Planets | Distance in Millions of Geographical Miles | Apparent Diameter in Seconds |
|---|---|---|---|
| 16 | Venus, | 20 | 62 |
| 18 | Jupiter, | 316 | 46 |
| 20 | Saturn, | 644 | 20 |
| 22 | Mars, | 28 | 23 |
| 24 | Mercury, | 160 | 12 |
| 26 | Uranus, | 1,392 | 4 |
| 28 | Pallas, | 88 | 3\(\frac{1}{2}\) |
| 30 | Juno, | 80 | 2\(\frac{1}{3}\) |
| 32 | Ceres, | 124 | 2 |
| 34 | Vesta, | 92 | \(\frac{4}{5}\) |
And for the time of Greatest Apogee
| Figs | Planets | Distance in Millions of Geographical Miles | Apparent Diameter in Seconds |
|---|---|---|---|
| 17 | Venus, | 140 | 9\(\frac{1}{2}\) |
| 19 | Jupiter, | 520 | 30 |
| 21 | Saturn, | 892 | 15\(\frac{1}{2}\) |
| 23 | Mars, | 216 | 3\(\frac{1}{3}\) |
| 25 | Mercury, | 120 | 4\(\frac{2}{5}\) |
| 27 | Uranus, | 1,696 | 3\(\frac{4}{5}\) |
| 29 | Pallas, | 368 | 1\(\frac{1}{2}\) |
| 31 | Juno, | 360 | 1\(\frac{1}{5}\) |
| 33 | Ceres, | 328 | \(\frac{4}{5}\) |
| 35 | Vesta, | 296 | \(\frac{2}{5}\) |
39. Pl. 14, figs. 36–45, exhibits approximately the apparent size of the sun, as seen from the planets at their mean distances from him. To this we will add the apparent diameters in seconds.
Apparent Size and Diameter of the Sun, as seen from the Planets
| Figs | Apparent Size in Order | Apparent Diameter |
|---|---|---|
| 36 | Mercury, | 1° 22′ 49′ |
| 37 | Venus, | 0° 40′ 32′ |
| 38 | Earth, | 0° 32′ 3′ |
| 39 | Mars, | 0° 21′ 2′ |
| 40 | Vesta, | 0° 13′ 35′ |
| 41 | Juno, | 0° 12′ 0′ |
| 42 | Ceres and Pallas, |
0° 11′ 34′ 0° 11′ 33′ |
| 43 | Jupiter, | 0° 6′ 10′ |
| 44 | Saturn, | 0° 3′ 22′ |
| 45 | Uranus, | 0° 1′ 40′ |
The figures above are also constructed on the scale AB, only the greatest divisions amount to 1500, the smaller to 150, and the smallest to 15 seconds. Hence it follows that to Uranus the sun appears 49\(\frac{1}{2}\) times smaller than to Mercury, and to Jupiter 5\(\frac{1}{2}\) times smaller than to the earth.
Finally, figs. 46–54 show the true diameter of the earth’s moon, and of these planets, compared with the true diameter of the earth. If in pl. 14, fig. 46, the diameter of the earth be taken as equal to 100 parts, then will the other diameters be as follows:—
- Moon of the earth, fig. 47, 26 parts
- Venus, fig. 48, 98 parts
- Mars, fig. 49, 52 parts
- Mercury, fig. 50, 39 parts
- Pallas, fig. 51, 26 parts
- Ceres, fig. 52, 20 parts
- Juno, fig. 53, 18 parts
- Vesta, fig. 54, 3 parts
Principal Phases of a Transit of Mercury or Venus over the Suns Disk, and manner of observing them.
40. The general theory of the transits of Venus and Mercury has been already explained in section 29, by reference to figs. 6, 7, 8, pl. 9. It still remains to show by fig. 55, pl. 14, the mode of observing such a phenomenon. When, as is generally the case, an astronomical telescope is employed, which represents all objects inverted, the attention of the observer, before the commencement of the transit, is to be directed to the right border of the sun’s disk. The straight line, passing through the figure, represents the course that Mercury, for instance, takes across the sun. When arrived at d, the first external contact of the limbs of Mercury and the sun, or the so-called external immersion, takes place; at this time the transit begins. Arrived at c, we have the first internal contact of the limbs of Mercury and the sun, or the so-called internal immersion; Mercury has now entered altogether on the disk of the sun. When the planet reaches b, the second internal contact, or the so-called internal emersion, takes place; at this moment the planet begins to leave the sun. Finally, the arrival of Mercury at a, brings about the second external contact, or the external emersion, the transit ceasing at this moment.
In reality, or when observed with the terrestrial telescope, these four phases follow in a direction from left to right; in other words, Mercury occupies in succession the points a, b, c, d. The case is precisely the same in a transit of Venus. The method of obtaining the sun’s parallax, and hence the mean distance of the earth from the sun, from such observations instituted at different places on the surface of the earth, cannot be here intelligibly exhibited and explained, as geometrical considerations combined with trigonometrical calculations are absolutely necessary.
The Total Eclipse of the Sun, June 4th, 1788
41. Fig. 56, pl. 14, furnishes a representation of the extent and course of the moon’s shadow over the earth’s surface during the existence of a total eclipse of the sun. For our illustration we have taken the total eclipse of the sun, which was observed on the 4th of June, 1788, in the eastern hemisphere of the earth. The figure represents, in the first place, a broad curved line or zone of intense black. This zone covers all places at which the total eclipse was seen. To all places in its very central line, the eclipse was annular and of longest duration, while the localities on its external border saw a total eclipse only for a moment. Parallel to this zone, and to the north and south of it, lines are drawn with these indications, 9, 6, and 3 digits obscuration, with corresponding shading. They include all those places where the eclipse affected 9, 6, and 3 digits of the sun’s disk respectively; to the north of the zone of total obscuration, the sun being eclipsed on its inferior, and to the south of it on its superior limb, and this in proportion to the proximity of the place to the central zone. The upper and lower arcs, GH and JK, cut all those places which saw, for a moment only, the beginning or the end of the entire eclipse. The arcs uniting the ends of GH and JK, cut the places which—the westerly at sunrise, the easterly at sunset—perceived just half the eclipse (or 6 digits). The other curved lines cut all those places where the beginning, the middle, or the end was perceived at sunrise, or the beginning, the middle, or the end at sunset. A glance at the chart consequently shows that this eclipse was visible in the whole of Europe and Asia, except Kamtschatka, the greater part of Siberia, and the island Celebes, as also in north and middle Africa.
42. The explanation of the origin and progress of eclipses of the sun and moon has already been given in section 22. To project any other great solar eclipse upon a map, as has been done in fig. 56, it will be first of all necessary to call in the assistance of a terrestrial globe, and likewise to obtain by previous calculation, several places on the earth’s surface, where, for a given time of the place, a central (total or annular) eclipse will happen. In other words, it will be necessary to know beforehand the course of the centre of the moon’s shadow over the earth’s surface. Cut from thin brass plate or pasteboard a circle, whose diameter is equal to the diameter of the globe, multiplied by the difference of the apparent radii of the sun and moon, and divided by the parallax of the moon. Next, place horizontally upon the globe a ruler, and upon the ruler the above-mentioned circle. Let A be a place on the globe, which for a given local time has the sun in its zenith, and let B represent a place which, according to the preceding calculation, is to see a central eclipse at this same time; adjust the globe in such a position that A occupies its highest point, and for this position of the globe, move the circle upon the inner horizontal ruler in such a manner that the centre of the circle shall lie perpendicularly above the point B. If we suppose straight lines to be drawn from all points in the circumference of the circle, perpendicular to its plane, then those vertically under the plane will inclose that space on the globe which, for the time in question, will be covered by the full shadow of the moon. We must now place the still horizontal ruler in such a manner that the centre of the circle shall constantly be vertically above the successive points B′, B″, B‴, &c., which for given times have a central eclipse. The globe must be turned at the same time in such a manner that its highest point is continually that which at the given times has the sun in its zenith. We can thus mark the entire path of the full shadow and its bounds on the globe, from which it may be transferred to a map. Cut now a circle whose diameter is equal to the diameter of the globe, multiplied by the sum of the apparent radii of the sun and moon, divided by the moon’s parallax, and proceed with this circle as before; we shall in this manner obtain all those places which lie before the northern and southern borders of the half shadow, and which consequently only perceive a contact of the edges of the moon and of the sun.
![]() Physical Astronomy
Physical Astronomy
Rotation of the Earth; its Spheroidal Form; Centrifugal Force; Simple Proof of the Spheroidal Shape of the Earth; Local Variation of Gravity
43. The daily motion of the starry heavens is only apparent, being a consequence of the actual turning of the earth on its axis, called its rotation. This rotation proceeds in a direction from west to east, since we see the apparent rotation of the heavens taking place in the opposite direction, or from east to west. Let, in fig. 7, pl. 6, the greater circle, KIHkih, represent the stationary heavens, and the smaller circle, the rotating earth with its centre C. The point o, in the upper part of the circle, will then, by its rotation, be made successively to assume the positions o, o. The consequence will be, that the horizon of o will be first Hoh, then Joi, then Kok, &c. The place o will consequently first see the part Hkih of the heavens, then JHki, then KJHk, &c. Now, since we do not perceive the motion of the earth, we are led to imagine that it is the heavens that move, which, however, is only an illusion caused by the earth’s rotation.
The flattened shape of the earth is also a consequence of its rotation. It is known from the theory of physics, that all parts of any body driven round in a circle with uniform velocity, endeavor to recede from the centre of this circle, which effort is called the centrifugal force. Let, in fig. 6, pl. 6, AMBN represent an elastic globe with an axis AB, passing through the centre C. If now the globe be turned rapidly about AB, all its parts will move the faster, the more remote they are from the poles A and B, or the nearer they are to the equator MN; A and B moving only on themselves as poles. With a more rapid motion there will be an increase of centrifugal force, and those parts of the globe lying near the points M and N will separate more from the axis of rotation AB. Hence the spherical globe, AMBN, will finally assume the ellipsoidal shape, mBnA, and appear depressed or flattened. The earth, when first set in motion, must have been in precisely the same condition as the above globe, assuming, however, that at that time its matter was in a fluid or semi-fluid state.
44. Thus the earth is not a perfect sphere, but an elliptical spheroid, in which the curvature of a meridian section at the equator is sensibly greater than at the poles, shown by measurements of degrees of latitude. Let NABDEF (pl. 6, fig. 9) represent a meridian section of the earth, C its centre, NA, BD, and GE, each a meridian arc, corresponding to a degree of latitude or to a degree of change in the meridian altitude of a star. Finally, let nN, aA, bB, dD, gG, eE, be the direction of the plummet at the places N, A, B, D, G, E, of which N is situated in the pole, and E in the equator. If now any two neighboring vertical lines, as nN and aA, bB and dD, gG and eE, be prolonged to their intersections in X, y, z, then the angles NXA, ByD, GzE, will each amount to a degree, and consequently be all equal. Thus the small arcs NA, BD, GE, may be considered as circular arcs described about X, y, z, as centres. The points X, y, z, are called the centres of curvature, and the lines XN or XA, yB or yD, and zG or zE, radii of curvature, by which the curvature at these points is determined and measured. Geometry teaches us that the intersections of all these vertical lines do not, as in the sphere, all fall in C, but must lie in a certain curve, Xyz, called the evolute. Experience has now shown that the terrestrial meridian is an ellipse, having for its major axis the equatorial diameter EF (fig. 9), and for its minor axis, the axis of the earth NS. This agrees also with the ratio of increase of the degree from the equator towards either pole. The radius of curvature at E is the least, that at N the greatest. The dotted lines in fig. 9 represent the parts of the evolute belonging to the other quadrants. It is to the celebrated Bessel that we owe the most recent and authentic results from measurements of degrees According to him, a mean degree of the meridian is equal to 57013.109 toises (364,576 English feet); half the major axis, or half the equatorial diameter to 3272077.14 toises (20,923,624 English feet); and half the minor axis, or half the axis of rotation to 3261139.33 toises (20,853,681 English feet). Consequently the flattening of the earth’s spheroid amounts to almost \(\frac{1}{300}\).
45. One important consequence of the centrifugal force is the local variation of gravity. It has actually been observed that there is a difference in the gravity or weight of the same body, when brought in succession to places of different geographical latitude. The methods by which these variations of gravity can be indicated, and their magnitude determined, are both statical and dynamical. The statical method consists in bringing the gravity of the weight in equilibrium with some natural force of entirely different character, upon which the local situation exerts no influence. Such a force is the elasticity of a spring. Let ABC (pl. 6, fig. 10) represent a strong beam of brass, standing on a firmly connected foot, AED. In this latter a flat plate of agate is inserted, and the whole foot rendered capable of being placed in a perfectly horizontal position by a water-level. To C is fastened the spiral spring G, carrying at its lower extremity the polished weight F, the length and strength of the spring being so adjusted that, even in the highest geographical latitude, the weight attached shall not at any time touch the agate plate D. If now the apparatus in perfect order be carried to a place of less geographical latitude, and again erected, it will soon be perceived that the weight F, loaded with the same additional weights as before, will no longer have power to stretch the spring to the degree necessary for bringing about contact between the weight and agate plate. It will therefore be necessary to add more weight, and this addition will evidently measure the difference of gravity in the two places, in so far as it operates on the sum of the suspended matter, that is, upon the sum of the weight F, and the half weight of the spiral spring G.
The dynamical method, on the other hand, consists in determining the velocity which is communicated in a second to a freely-falling body, by that force which draws a given heavy body to the earth. This velocity can only be determined indirectly by observations, as the oscillation of a pendulum. It is shown by the laws of mechanics, that when the same pendulum oscillates in two different places, and consequently under the influence of different forces of gravitation, the intensities of gravitation will be to each other as the squares of the numbers of oscillations made in a given time, and hence their ratio is readily determinable.
Compound Motion; Parallelogram of Forces
46. Two or more forces acting on the same body in different directions cause it to assume a compound motion. If, however, these forces act on each other in such a manner that no motion can result to the body, they are said to hold one another in equilibrium. If any two forces act upon the same body in directions forming a known angle with each other, and with known intensities, it is evident that in its course it can obey exclusively neither the one nor the other of these forces. We must therefore investigate the direction and velocity with which the body will move forward, This is easily done by representing the given directions and velocities by the two straight lines, AB, CD (pl. 6, fig. 11), completing the parallelogram ABCD, and drawing its diagonal AD. AD, by its position with respect to AB and AC, will then give the desired direction, and by its length the desired velocity of the motion of the body. This construction, so important in mechanics, is called the parallelogram of forces; AB and AC, the lateral forces; and AD the mean force, the resulting force, or simply the resultant. It has been previously mentioned (section 32) that in astronomy a very important application is made of the parallelogram of forces.
Refraction; Morning and Evening Twilight
47. Refraction or bending of rays is of great importance in astronomical observations, as it causes the apparent to differ from the true altitude of a star. The atmosphere, like any other transparent body, turns an obliquely incident ray of light, SA (pl. 6, fig. 17), from its rectilineal direction—in other words, it bends it. Thus a ray of light, SA, coming from a rarer medium (the ether), and incident at a point, A, upon a denser medium (the atmosphere), is bent towards the perpendicular BAC at the point of incidence, just in proportion to the density of this medium into which the light passes. Suppose now an observer to be situated at any point, A, of the earth’s surface, KAk (fig. 16); furthermore, let Ll, Mm, Nn, represent successive strata of decreasing density, into which the atmosphere may be supposed to be divided, these evidently being spherical layers conpentric with the earth’s surface, KAk. Finally, let S represent a star beyond the external limits of the atmosphere. If now there were no atmosphere, the observer at A would see the star in the direction of the straight line AS. In reality, however, the ray SA begins, as soon as it reaches the atmosphere at d, to take a more inclined direction, dc, according to the above-mentioned law of dioptrics. This change of direction at first, owing to the extraordinary rarity of the outermost layers of the atmosphere, is very slight, but increases as the ray approaches the earth, entering successively into denser and denser strata, and the refraction becoming accordingly greater and greater. Thus, instead of following the rectilineal direction SdA, it describes a curve Sdcba, which becomes more and more concave, finally reaching the earth, not at A, but at a point a, nearer to S. This ray consequently does not come to the eye of the observer. The ray by which the observer at A perceives the star S, is not SdA, but another ray, which, in the absence of an atmosphere, would have reached the point K, behind the observer. Now, however, by the refractive power of the atmosphere, it is bent into the curved line SDCBA, actually reaching the earth at A. It is a well-known law in optics, that every object is seen in the direction which the way from the object has at the time of its entrance into the eye, the intermediate course of the ray not coming into account. The star S will therefore be seen, not in the direction AS, but in the direction of the straight line As, tangent to the curve SDCBA at A. Since the curve described by the refracted ray has its concavity inferior, the tangent line As must lie above the unbroken ray AS; consequently the star S will, by means of the refracting atmosphere, appear higher above the horizon AH than it would were there no such atmosphere. Moreover, since the direction of the strata of air is the same in every direction about A, the ray cannot deviate laterally, but must always remain in the same vertical plane, SAC′, passing through the eye, the star, and the centre of the earth.
From what precedes it is evident that refraction causes all the heavenly bodies to appear higher than they really are. Therefore, a star actually below the horizon may, by refraction, be raised above it, and become visible, which could not occur without the refracting atmosphere. Thus, for example, the sun, when actually at P, below the horizon AH of the observer, may be rendered visible by the curved line PqrA, of which Ap is the tangent, so as to be referred to p. The amount of the astronomical refraction (to be distinguished from terrestrial refraction), for any given altitude in the heavens, depends mainly upon the character, density, temperature, and moisture of the atmosphere; and for this reason the accurate determination of refraction for all heights, particularly for moderate ones, is one of the most difficult problems of physical astronomy. The following general considerations alone can here be mentioned: In the zenith there is no refraction, that is, it is equal to Zero; consequently, a star directly overhead will be seen in its true direction, or as if no refracting atmosphere surrounded the earth. The astronomical refraction increases from the zenith to the horizon, at first very slightly, afterwards more decidedly, so that a star situated near the horizon will appear more distant from its true place than one at a greater altitude. The mean amount of refraction for a celestial body, midway between the zenith and horizon, or at an altitude of 45°, is only 57 seconds, an amount scarcely sensible to the naked eye; but in the horizon, where refraction is greatest, it amounts to 33 minutes, which is more than the greatest apparent diameter of the sun or moon.
48. A prominent consequence of the refraction and deviation of the rays of light is the morning and evening twilight. Night, as is well known, does not immediately follow the day, nor the day night; after the setting of the sun, his rays still penetrate the higher regions of the atmosphere, losing themselves in space. The night thus comes on gradually. This prolongation of day is known commonly as twilight, produced partly by reflection, partly by refraction. Let SO (fig. 22, pl. 6) be a ray of sunlight entering the atmosphere at O; then, instead of following the original direction, and leaving the atmosphere at M, it will be diverted from its course or become broken. This deviation will be the greater the further the ray penetrates into the lower strata, which are denser as they are situated nearer the earth, so that the ray will describe the curve OG. In like manner, the ray SZ will become a curve from Z to D. Since, as has already been shown in pl. 6, fig. 16, this refraction is most considerable in the horizon, the sun appears to rise earlier and set later than is actually the case, by which means the day is lengthened and the night shortened. Before the rising of the sun, a part of his light will be reflected from the atmosphere to the surface of the earth. Thus, in fig. 22, let MGBD be the earth, and G a point on its surface for which the sun is just about to rise. It is now evident that the horizon HGR, of the point G, receives light from every part of the heavens, whether direct or reflected; consequently the point A, for which the sun has not yet risen, has above its horizon the indirectly illuminated part, KLR, of the heavens. The morning redness is more brilliant at K, becoming gradually feebler towards R. The point B, on the contrary, has no light at all, and it is there midnight. The cause of evening twilight may be explained in the same manner, and it will be perceived that for the point D, where the sun is just setting, the whole horizon is still bright; while for the point C, the part TNX of the heavens is only indirectly illuminated. A circle in the heavens, parallel to the horizon, and at a distance of 18° below it, is called the crepuscular circle, or circle of twilight.
Let the point M (fig. 22) represent Leipzig, and the time be exactly noon; for the place G, situated 90° west, it will be past 6 o’clock A.M.; for the place Y, 45° west, it will be 9 o'clock A.M.; and to this latter the sun, on account of refraction, will appear at J. It will moreover be seen that for a place III., situated 45° east, the sun will appear at E, and that it will there be already 3 o’clock P.M. Finally, it will be readily understood, that while the earth moves about its axis, whose north pole is P, from west to east, or in the direction of the arrows, it must seem as if the sun, in an inverse order, attained successively the points F, J, S, E, U. Fig. 22 has been drawn to represent the time of the equinox, when the sun appears to describe the equator.
The morning and evening dawn or twilight is, in conclusion, not only more or less different in the same place at different seasons, but also different at places of different latitudes for the same season.
The Tides
49. Another very remarkable phenomenon, produced by the attraction of the sun and moon upon the surface of the earth, is the ebb and flow of the tide, that well-known and generally regular motion of the sea, which results in a considerable variation of its height twice every day. On the coast of a great and open sea, as the North Sea, the phenomena of ebb and flow will take place in the following manner:—At the time when the water is highest, or at high tide, no change will be perceptible for some minutes. Gradually the water begins to run off westward, slowly at first, then with a continually increasing velocity, which reaches its maximum in about three hours. After this the fall continues for three hours with decreasing velocity, so that in a little more than six hours from the time of highest tide, low tide takes place. The sea, after remaining at this stage for some minutes, again begins to rise for six hours, and indeed in the same manner as it fell, so that in a little more than six hours from low tide, high tide again prevails. The rise of the water is called the flow of the tide, and the falling the ebb. In this manner the whole phenomenon is incessantly repeated in periods of 12 hours and 25 minutes. The difference of elevation of the water at high tide and at low tide is not the same in all places at the same time, nor in one and the same place at all times. This difference, for example, on the German coast of the North Sea, amounts to 13 feet; while at the western end of the Straits of Dover it is sometimes more than 40 feet. The position of the coast, and the direction of the wind, change not a little the regular course of the whole phenomenon. Apart, however, from these local and temporary influences, a monthly and a yearly period are plainly evident. There is a greater difference between high and low water at the time of new and full moon, than at the time of the quadratures; and furthermore, this difference is more considerable when the sun and earth are nearest to each other, than when most remote. From this there cannot be the slightest doubt that the sun, and more particularly the moon, produce the ebb and flow of the tide.
For the proper elucidation of this phenomenon, suppose the earth’s surface to be covered equally with water, and let us inquire what shape this watery surface will assume when the earth, on account of the attraction, begins to fall towards the moon; we will here have reference only to the influence of the latter, as being the most important. It is evident that those portions of the water will be attracted the strongest, which lie nearest the moon M (pl. 6, fig. 23), and consequently the water surrounding the earth will be heaped up highest at that place, O, which has the moon in its zenith. Here, then, where a mountain of water has arisen, the height of the water will be greatest, decreasing, however, more and more in every direction reaching the minimum at those points, Z and Z′ (at time of full moon V and V′), which have the moon in the horizon; at the point O′ of the earth, which has the moon in its nadir, there will also be an elevation of the water: this point will be attracted least, and consequently will remain further behind the other points. Hence it follows that there will be a rise of the water at the two points, O, O′, of the earth, distant a whole diameter from each other, and lying in the straight line connecting the centres of the earth and moon. From these two points, the height of the water will decrease according to a certain law, until finally it will be lowest in the points of that great circle which has the two points of highest water for its poles; that is, as before mentioned, in all those places which have the moon in their horizon. Now, although the earth is not a globe entirely surrounded by water, yet by far the greatest portion is covered with water; and the waters of the sea will thus be heaped up in those points which have the moon in the meridian, whether at the inferior or superior culmination. Since the moon, on account of its own motion and the rotation of the earth, culminates every 12 hours and 25 minutes for one and the same place, the phenomenon known as the ebb and flow must continually return within this period. Nevertheless, the time of flood does not exactly coincide with that of the culmination of the moon, which at first may appear strange; but when we reflect that on account of the inertia of the material, the mass of water cannot immediately follow the apparent motion of the moon, that apparent anomaty will be explained. That the flow in different places of the earth follows sometimes sooner, sometimes later, the culmination of the moon, is to be ascribed to local causes, as has been satisfactorily ascertained by means of many accurately conducted experiments.
Not only the moon, but also the sun, exercises an attraction on the water, and the attractive forces of the sun and moon must co-operate at time of new and full moon, and act against each other in the quadratures. That at full moon a high tide must, occur, might at first appear singular, until explained by the fact that, on the side of the earth opposite to the moon, an elevation of the water necessarily occurs. Thus is explained the monthly period of ebb and flow. The tides occurring at the time of the syzigies in O and O′, are commonly called spring tides; those at the quadratures E, E′, neap tides.
Finally, there are several causes of the yearly period of ebb and flow, but we shall here only mention those which depend on the varying distance of the sun from the earth. Higher tides will take place in the winter than in the summer months. Since the moon can never separate more than 30° from the celestial equator, it is evident that within that terrestrial zone included between 30 degrees of north and south latitude, the tides must be greatest. This is confirmed by observation, since in the polar seas the entire phenomenon disappears. From what has been said, the conclusion is readily deducible—that the ocean alone, with the open and large seas in connexion with it, can have tides; for supposing the moon to be above the Caspian sea, for instance, then its waters will be attracted; yet, on account of the small extent of surface, this lunar attraction will be everywhere equal, so that an elevation of any particular part cannot take place.
The Resistance of the Ether; its Influence on the Motion of Comets
50. The apparent course of the inferior and superior planets has already (pl. 6, figs. 24, 25) been explained. Some attention will here be directed to a circumstance of great importance to the planets, and particularly to the comets. For a long while it was believed that the spaces between the heavenly bodies were absolutely empty, or that a perfect vacuum existed there. This supposition, however, does not seem to be confirmed, at least with respect to the interspace of our planetary system. It is well known that all bodies fall with equal velocity in a perfect vacuum: moreover, the denser the air, and the rarer the body moving in it, the more readily the latter loses its original velocity, since it must experience a greater resistance than another body of greater density moving in the same medium. This must be true with regard to the planets. As these have shown no diminution in their velocity produced by the resistance, we must suppose one of two things: either that the interspaces of our planetary system are absolutely empty, or that if a medium really exists, it is much too rare, in comparison with the density of the planets, to produce any retarding influence on their motions. The comets, however, which are known to be bodies of very slight density, may experience some retardation, even if it be very slight, from the rare ether existing in space. The continual abbreviation of the period of revolution of Encke’s comet, already several times returned, observed, and calculated, indicates conclusively enough that space is filled by a medium, and consequently is not absolutely empty. This abbreviation of the period of the above mentioned comet, is evidently a consequence of the resistance which the ether opposes to the course of the comet. The comet itself may by this means experience, one day or other, a very destructive catastrophe. Since it meets a resistance in its course around the sun, it naturally will not be able to retain its original orbit, but must by degrees move in arcs which lie nearer to the sun than those previously described in similar times. The orbit will, therefore, remain no longer an ellipse or a closed curve, but must become a spiral, terminating in the sun itself, since the comet will be more and more affected by his attraction, and consequently approach nearer and nearer (pl. 6, fig. 26). The immediate consequence of this must be a gradually diminishing period of the comet, which will accomplish its course with greater and greater velocity, until finally it will be lost in the sun.
The Sun’s Spots
51. Pl. 9, figs. 9–13 represent the black spots seen sometimes, with the assistance of the telescope, on the sun’s disk, of greater or less size, irregular shape, and surrounded by an ash grey border, generally of uniform breadth. The solar spots appear frequently to change not only their shape, as shown by figs. 10 and 11, but also their position on the sun’s disk. They are sometimes very large, and their constant occurrence in connexion with the solar faculaœ (fig. 9), as also their ash grey border, plainly indicate a common origin with these. Thus, for instance, their black spots may be seen to break out in the midst of these faculse, or, inversely, faculse arise in the places whence spots have just vanished. These facutœ are streaks, which, by their dazzling light, are distinguishable from the rest of the disk, and resemble, so to speak, veins of light.
It is very rare that the spots on the sun are seen at a distance of more than 30° from his equator on each side. At their entrance on the sun’s disk they appear very small, and when they come near to the border of the sun, they are seen as black lines, becoming broader the nearer they are to the centre of the disk; they moreover seem to move in almost parallel lines from east to west over the sun’s disk: their true motion, however, is from west to east, as they would appear to an eye at the centre of the globe of the sun. A spot generally occupies from 12 to 13 days in crossing the visible disk of the sun. It is then invisible for a period of 14–15 days, but at the expiration of this time it appears in the same place in about 27 or 28 days after the first appearance, to commence its second revolution. The paths of the spots appear towards the 10th of June and 10th of December as straight lines; on all other days of the year as ellipses, whose convex sides are turned for half a year towards the north, and for the same length of time towards the south, and whose greatest curvature takes place shortly before March 10th and September 10th. Observations on the sun’s spots have enabled us to ascertain a rotation of the sun on its axis in a period of 25\(\frac{1}{2}\) days.
Herschel’s hypothesis with respect to the nature of the spots on the sun, appears to be the most probable. He assumes a threefold concentric envelope of the obscure body of the sun proper. This first envelope is the photosphere, or atmosphere of light; beneath it the second, a transparent and very elastic medium; and beneath this layer the third, a cloudy obscure envelope, illuminated on its outer side, and reflecting the light to our eyes. In this manner it forms an ash grey border, which is seen sometimes on the sun without a central spot, whenever an opening may exist in the first, or first and second layers. Whenever this fissure or opening extends, as is generally the case, through the third layer, the dark nucleus of the sun is then perceived, and about it the above mentioned grey border, which is, accordingly, nothing else than the light passing into the opening from the outermost layer, and reflected back from the inner atmosphere to our eye.
The group of spots represented in fig. 9, was discovered May, 1799, by Fritsch of Quedlinburgh. The western spot, very near the border of the sun, appeared as a black nucleus of oval shape, with an equally oval nebulous inclosure. Eastward of the oval spot, Fritsch observed another circular one, both united by a so called valley or mountain way, having the appearance of a ring mountain of our moon. From this mountain way run lateral branches, and both appear to the eye whiter and fainter than the rest of the solar surface. The spots, pl. 9, figs. 10, 11, 12, 13, were discovered by Pastorflf, in Frankfurt on the Oder, May 24th, 1828. The largest (fig. 10), abcd, had at ab a diameter of 100 seconds, and at cd one of 60. It now appears, however, as a straight line of 392 geographical miles on the surface of the sun, under an angle of almost one second, seen from the earth; consequently, the true diameter of this spot amounted to 39,200 geographical miles at ab, and to 23,520 at cd. The greatest diameter amounted to more than five diameters of the earth (= to 6880 geographical miles), consequently the surface of this spot contained nearly 928,000,000 square geographical miles. Furthermore, ef (fig. 10) had an apparent diameter = 110 seconds; gh = 60; no = 68; pq = 30; ik (fig. 11) = 38; lm (fig. 12) = 66; rs = 24; tu (fig. 13) = 46; and wx = 12. All these numbers multiplied by 392 give the dimensions in geographical miles, altogether equal to an area of 2,496 millions of square geographical miles, or about 17 times as great as the whole surface of the earth.
The honor of the first discovery of the sun’s spots appears due to the English astronomer, Harriot, who saw them Dec. 8, 1610. The eminent physician Averrhoes (in the twelfth century) was perhaps the first who saw a spot with the naked eye, erroneously supposed by him to be the planet Mercury. Phrystus of Wittemberg published the first treatise on these spots in 1611; the Jesuit, Father Scheiner, however, sought to appropriate the discovery. He seems to have exhibited, in May, 1611, the first spot to his pupils in Ingolstadt, where he was professor. Galileo had observed the spots of the sun as early as the beginning of 1611, nearly contemporaneously with Fabricius, and very soon presented correct views of their nature.
Topography of the Moon
52. The most interesting object visible by a good telescope in the heavens, is certainly the surface of the moon, whose peculiarities, as being of all heavenly bodies the nearest to us, are known best of all. At an early period Galileo, Scheiner, and Hevelius, and afterwards Grimaldi, Riccioli, Cassini, and Lahire, attempted to construct a chart of the moon; the maps of the moon by Hevelius, Mayer, and Schroter, are well known. Lohrmann, however, uniting an intimate knowledge of facts with sound judgment, first published accurate and beautiful maps of the moon, four in number, whose continuation was unfortunately arrested by his death. Beer and Madler, finally, in 1836, published four large sheets with a general map of the moon, on Lohrmann’s plan, indeed, but founded on original observations. Of this general map pl. 11, fig. 1 is an accurately reduced copy. Our chart represents the moon inverted, or as it would be exhibited to the observer in an astronomical telescope of from 60 to 80 magnifying power. North is consequently below, South above, East to the right, and West to the left. From want of room, and to avoid crowding, the single mountains and craters are indicated by numbers, whose import will presently be explained. On the moon there can be directly distinguished nothing but differences of level and illumination; consequently only mountains, craters, and colors. The two first are exhibited best in the growing and waning moon, when the part to be observed lies near the illuminated border; the colors we see to the most advantage at the full moon. Many of the ring mountains have, following Riccioli’s example, been named after eminent philosophers; while for the rest, with Hevelius, the names of mountains, rivers, &c., have been borrowed from the earth.
53. The numbers annexed to the names in the following list, indicate the depth or the inner descent of the wall in Paris feet; where a second number, inclosed in brackets, occurs, it indicates the height of the wall above the outer inclosure. All these numbers are derived from original measurements by Beer and Mädler.
I.—Northwestern Quadrant of the Moon
The Map of the Moon (pl. 11, fig. 1) to the Left Below
- Schubert
- Reper
- Firmicus4638
- Apollonius5100
- Taruntius3272
- Maskelyne4362
- Sabine2485
- Ritter3718
- Dionysius
- Arago5022
- Sosigenes
- Cæsar5082
- Ariadäus
- Godin6780
- Agrippa6342
- Boscowich
- Hyginus
- Rhäticus
- Triesnecker5086
- Uckert
- Condorcet8410
- Hansen
- Alhazen
- Azout5300
- Picard4982 (2867)
- Proclus7790
- Jansen
- Vitruvius4227
- Maraldi
- Plinius5904
- Ross
- Acherusia ape4536
- Taquet
- Menelaus6164
- Sculpic. Gallus
- Manilius7223
- Agarum Cape9666
- Eimmart9683
- Oriani
- Plutarch
- Seneca
- Hahn9095
- Berosus10,722
- Cleomedes8194
- Tralles8202
- Macrobius14,409
- Römer10,864
- Littrow
- Lemonnier8475
- Bessel3606 (1464)
- Linnæus
- Conon
- Hadley14,208
- Bradley12,639
- Gauss
- Burckhardt13,672
- Geminus11,577
- Bernouilli11,868
- Messala3,360
- Berzelius
- Franklin7,436
- Posidonius5346 (2976)
- Kalippus7,230
- Theätetus7004 (3312)
- Aristillus10,464 (4750)
- Autolycus8457 (4485)
- Cassini4098 (3870)
- Struve
- Schumacher
- Mercurius
- Hook
- Cepheus8588
- Oersted
- Atlas10,261 (3462)
- Hercules10,209
- Mason5705 (3336)
- Plana
- Bürg6372 (4297)
- Eudoxus13,980
- Aristotle10,031 (4266)
- Egede320
- Endymion15,690
- Strabo
- Thales
- Gärtner
- Democritus5302
- Christ. Mayer3906
- Meton
- Euktemon
- Scoresby9216
- Barrow8832
- Archytas3704
II.—Northeastern Quadrant of the Moon
The Map of the Moon (pl. 11, fig. 1) to the Right Below
- Pallas4193
- Bode
- Schröter3640
- Gambart2500 (2154)
- Stadius630
- Copernicus10,584 (2478)
- Reinhold8819
- Hortensius
- Encke1698
- Kepler9400
- Reiner9306
- Hevelius
- Cavalerius8990
- Olbers
- Marco Polo
- Eratosthenes14,678 (6204)
- Gay-Lussac
- Mayer
- Milichius
- Marius4270
- Bessarion
- Cardanus
- Kraft
- Huyghens16,934
- Woff11,316
- Archimedes5084 (3636)
- Timocharis6786 (3436)
- Pytheas(5500) (2241)
- Lambert5580 (2259)
- Euler5585 (1062)
- Diophantus4000 (2392)
- Lahire4788
- Herodotus4032
- Seleucus
- Briggs
- Aristarchus7058
- Helicon2482
- Carlini
- Delisle5586
- Wollaston
- Lichtenberg
- Lavoisier
- Kirch
- Pico6624
- Laplace9022
- Heraclides3,681
- Maupertius
- Bianchini7,936
- Sharp6,949
- Mairan7520 (4890)
- Louville
- Gerard
- Plato6,810
- Lacondamine3996 (2490)
- Bouguer
- Harpalus14,872 (2576)
- Œnopides
- Repsold
- Harding
- Xenophanes
- Cleostratus
- Timäus
- Epigenes
- Fontenelle6372
- Horrebow
- Anaximander
- Pythagoras
- Gioja
- Anaxagoras8943
- Philolaus11,604
- Anaximenes7487
- Sömmerring4282
- Vasco de Gama
III.—Southeastern Quadrant of the Moon
The Map of the Moon (pl. 11, fig. 1) to the Right Above
- Malapert
- Cabeus
- Short17,532
- Moretus14,994
- Newton22,362
- Casatus19,514
- Klaproth9365
- Wilson12,954
- Gruemberger13,024
- Cysatus11,900
- Blancanus16,892
- Scheiner
- Kircher16,530
- Bettinus11,616
- Bailly13,910
- Hausen
- Zuchius
- Clavius15,792
- Deluc
- Maginus13,553
- Longomontanus13,641
- Rost7406
- Weigel
- Segner7617 (6006)
- Bayer7572
- Schiller11,856
- Phokylides8250
- Wargentin(400) (1392)
- Saussure
- Pictet
- Street4188
- Sycho16,662
- William I.10,389
- Heinsius8130
- Hainzel10,880
- Drebbel
- Schickard7938
- Inghirami11,460
- Lehmann
- Nasireddin10,308
- Orontius
- Sasserides7415
- Lexell7236
- Walter13,749
- Hell5034
- Gauricus8730
- Wurzelbauer5160
- Pitatus
- Hesiodus
- Cichus7938 (4848)
- Capuanus8022
- Ramsden3000 (1722)
- Vitello4000 (4810)
- Piazzi
- Lagrange
- Bouvard
- Regiomontanus9564
- Purbach7594
- Thebit7882
- Mercator4358
- Campanus6126
- Hippalus
- Kies2292
- Bulliald8410
- Doppelmayer
- Fourer8877
- Vieta13,739
- Cavendish7038
- Byrgius6516
- Mersenius7890
- Eichstädt
- Arzachel12,750
- Alphonso6600 (5196)
- Alpretagius11,291 (3540)
- Davy
- Guericke1926
- Lubiniezki924
- Agatharchides3456
- Gassendi8970
- Letronne3015
- Billy3183 (2992)
- Zupus4399
- Lontana
- Sirsalis9528
- Crüger
- Rocca
- Ptolemäus7452
- Herschel8832
- Mösting7062 (1524)
- Lalande
- Parry1536
- Bonpland
- Fra Mauro
- Landsberg9064 (2802)
- Euclides
- Flamsteed5479 (1320)
- Damoiseau
- Grimaldi
- Lohrmann
- Riccioli
- Hansteen3522 (2649)
IV.—Southwestern Quadrant of the Moon
The Map of the Moon (pl. 11, fig. 1) to the Left Above
- Schomberger
- Simpelius9645
- Boguslawski10,468
- Boussingault
- Manzinus9991
- Mutus11,525
- Pentland
- Curtius
- Pontecoulant
- Hanno
- Biela
- Hagecius
- Nerchus
- Rosenberger
- Blacq9762
- Hommel
- Pitiscus9463
- Baco11,616
- Jacobi9684
- Zach11,414
- Lilius9286
- Oken
- Vega
- Steinheil11,046
- Fabricuius7818
- Nicolai5874
- Clairaut
- Barocius11,366
- Maurolicus13,314
- Cuvier11,272
- Licetus12,766
- Stöfler10,950
- Marinus
- Faunhofer
- Furnerius10,100
- Stevinus10,782
- Rheita13,464
- Metius12,372
- Reichenbach10,996
- Neander7476
- Stiborius11,343
- Riccius
- Rabbi Levi
- Zagut
- Lindenau11,136
- Büsching4218
- Buch
- Gemma Frisius12,796
- Poisson6888
- Aliacensis13,624
- W. von Humboldt
- Hekateus
- Legendre7627
- Petavius10,158
- Snellius6400
- Borda10,338
- Fracastoro7988
- Santbech12,894
- Piccolomini14,574
- Polybius7278
- Pons
- Fermat
- Sacrobosco11,295
- Ponanus
- Azophi13,644
- Abenezra10,254
- Appianus8787
- Playfair11,290
- Werner14,658
- Ansgarius
- Vendelinus5046
- Cook2959
- Colombo7540
- Magellan
- Bohnenberger
- Beaumont5778
- Thophilus14,939
- Cyrillus
- Katharina15,423
- Kant
- Tacitus9762
- Almanon5724
- Geber8112
- Abulfeda9600
- Airy
- Albategnius13,943
- Parrot
- Kästner
- Maclaurin
- Langrenus11,616
- Messier5256
- Goclenius4386
- Gutenberg
- Capella9504
- Isidor9005
- Torricelli
- Hypatia6904
- Delambre14,046
- Hyparchus
- Réaumur
- Biot
- Lacaille
54. With only a tolerably good telescope, the bright spots of the moon can be determined as mountains, by means of their shadows. Their shadow lies always on the side opposite to the sun, and is the longer the less the altitude of the sun for the mountain. The grey spots were at one time erroneously supposed to be seas. The distinct brilliant points, so many of which are seen on the full moon, are only rarely elevations; oftener steeply precipitous depressions. The structure of the lunar mountains in general is very different from that which prevails on our earth, in that they present themselves for the most part as circular closed walls, with a hollow sloping cavity. They are called ring mountains, as, for instance (pl. 11, fig. 1), Ptolemaeus (III. 87), Alphonso (III. 73), and Archimedes (II. 26); Plato (fig. 4). The greater of them are called walled plains when they inclose a plane surface: the smallest ring mountains are called craters. The most diminutive of these, on account of their small size, could not be represented in pl. 11 by mountain streaks, and therefore small circles have been employed for these. They are seen on a larger scale in fig. 3, namely, Pliny and Vitruvius. The walled plains occurring most frequently in the southwestern part of the moon, appear to belong to the earlier formations of the moon’s surface, since they are unmistakably inferior to later forms of every kind. The light streaks passing frequently through walled plains, as also over the other regions of the moon, are not, as a whole, actual elevations, as they are sought in vain under an oblique illumination, when actual elevations are indicated as such by their shadows.
Next to the walled plains follow, in order of size, the ring mountains proper, which, often truly circular, exist in great numbers. Frequently their wall slopes inwards and outwards in so called terraces; and in their interior, they generally present an elevation known as the central mountain. The most of these central mountains, however, do not reach as high up as the wall. Where the central mountain stands, the inside is sometimes dark grey; commonly, however, as bright as the outer wall. In the southern hemisphere of the moon, the most of these mountains with their walls and environs are so much alike in color and light, that at full moon nothing more can be distinguished of them. The same thing occurs frequently in the deepest, most conspicuous, and most varied ring mountains and walled plains, sometimes even in the grey spots. These latter, consequently, as for instance in fig. I., Mare Crisium, Mare Fcecunditatis, Mare Tranquillitatis, and Mare Serenitatis, cannot possibly be seas. Hence it also follows that the view of the full moon is entirely different from that at the first or last quarter, since here the shadows of the mountains and craters present themselves, while there it is only various colors and their shading that are seen.
Mountain chains occur here and there upon the moon, as upon the earth, but never of so great length. Even those mountains connected with one another, and termed mountain chains, have by no means the same valley and hill structures as the mountain chains on our earth, but they approach more to the crater form, and do not run out into various branches. The names of these mountain chains have been derived from those on the earth, as may be seen on the maps of the moon (pl. 11, fig. 1). The greatest elevations of the following mountain chain are given in Paris feet.
- Caucasus17,138
- Appenines16,934
- Altai12,459
- Mountain on Sinus Iridum14,022
- Pyrenees11,178
- Alps11,136
- Taurus8,472
- Hemus6,222
- Carpathians5,970
- Riphæans2,580
Again, perfectly insulated mountains, called cone mountains, exist in great numbers on the moon. With respect to the grey level regions of the moon, at one time called seas, they are universally intersected by ranges of heights, either long and straight, or running in great free curves. The latter are with some inaccuracy termed mountain spurs, since they are not ramifications and extensions of greater mountains, and vanish entirely at full moon, casting a shadow only at sunrise and sunset, by which they are then recognised. The streaks of light must be considered as very remarkable and difficult of explanation, many of which run along singly, but most form radiating systems. These streaks of light stretch indifferently over mountains, valleys, and plains, without altering their shape, direction, or color. They are almost always four to twelve miles broad, and vanish under an oblique illumination. Equally singular are the channels, those extremely narrow but deep furrows, which run generally in rectilineal directions through plains, and more rarely through mountainous regions. These channels cannot be streams or their beds, nor can they remind us of canals and highways. These channels are indicated by narrow parallel lines on the map of the moon.
As regards the colors of the moon, we can only indicate them on our chart in the most general outlines. At least ten different shades, from dark grey to the most brilliant white, can be distinguished. In general, the elevation is the brighter, and the depression the darker; this relation is, however, sometimes inverted. The brightest spots very rarely belong to the higher mountains; it is rather great depths that shine with uncommon brilliancy.
55. For the sake of giving a clear idea of the appearance of particular regions of the moon through a good refractor of 200–300 magnifying power, we have furnished the figures 2, 3, 4, and 5, which surround fig. 1, pl. 11. The region fig. 2 contains the mountains Caucasus, Calippus, Eudoxus, and Aristotle, found in quadrant I. (fig. 1); fig. 3, the mountains Jansen, Plinius, Vitruvius, and Littrow, with a part of Mare Serenitatis, also occurring in quadrant I. Fig. 4 represents the mountains found in quadrant II. (fig. 1), namely, Kirch, Pico, Alps, Plato; as also a part of Mare Imbrium and of Palus Nebulum. Finally, fig. 5 represents the mountains Saussure, Pictet, Tycho, Sasserides, and Gauricus, of quadrant III. (fig. 1.)
A degree of the equator, or \(\frac{1}{360}\) part, is equal to 60 geographical miles; a degree of the moon’s equator is equal to 16 \(\frac{36}{100}\) geographical miles; the whole surface of the moon is therefore about equal to the area of America.
The visible hemisphere of the moon is represented in fig. 1, pl. 11, as it appears at the time of mean libration. Consequently only the central parts appear in their true proportions; for nearer the borders all circular crater groups must appear oblong.
It is erroneous to suppose that with better instruments and higher magnifying powers, it will be hereafter possible to perceive more and minuter details of the moon’s surface (as, for instance, artificial structures) than at present: for with these improvements the difficulties and hindrances will increase in like proportion. We need only refer to the atmosphere of the earth and the borrowed light of the moon. These difficulties are even now experienced in the application of the best telescopes, as the moon, of all the heavenly bodies, is that for which the highest powers are unsuited. It is by means of very accurate and long continued observations that we are to have our knowledge of the moon increased. It is only then that better comparisons with the earlier observations, and more accurate conclusions may be drawn than now, when only since the time of Lohrmann and Mädler the moon has been attentively examined with the more improved refractors. Posterity will be able to verify changes which appear to be taking place on the surface of the moon, and our successors will probably ridicule many of our opinions, and reject them as untenable. One fact is certain, however, that Selenography (description of the moon) must commence with generalities and progress to particulars, while Geography (description of the earth) pursues the opposite method. Selenography has the advantage of Geography, as we do not possess so good a general view of the earth as of the half of the moon which is visible to us.
To become most readily acquainted with the mountains, craters, &c., of the moon, it will be necessary to examine attentively the moon at the time of the first or last quarter, through a telescope of about 40–60 magnifying power, and to make constant reference to the lunar maps. During the full moon, this, at least to a beginner, is not very satisfactory, as at this time the sun stands directly over the centre of the visible moon’s disk, and the shadows of the mountains are not seen. In the first and last quarters, however, the sun moves above and below the centre of the visible disk, and at this time, accordingly, the shadows of the mountains are greatest and most evident.
The Planets Mars, Jupiter, Saturn, and Uranus
56. Pl. 8, fig. 18, represents the planet Mars in his not entirely illuminated condition, as seen August 16, 1830, by Sir John Herschel, at Slough, with a 20-foot reflector. We see plainly enough presumptive continents and seas; the first distinguished by their reddish color, characterizing the light of this ever red and fiery planet. In contrast with this color, the seas, if we may so term them, appear of a greenish hue. These spots cannot always be seen with equal distinctness, which is probably owing to the fact of Mars not being entirely free from an atmosphere. This supposition is confirmed by the exhibition of brilliant white spots at the poles of Mars. These spots are probably snow, as they vanish when they have been long exposed to the sun, and on the other hand are largest on emerging from the long night of their polar winter. By observations on the spots, Mars has been found to have a period of rotation in 24 hours, 39 minutes, 21 seconds; and the inclination of the axis of rotation to the ecliptic, amounts to about 30° 18′.
Since the time of Herschel and Schröter, Mädler in Dorpat has first, in our day, carefully and attentively examined the surface of Mars. It is moreover known that Mars alone of all the superior planets exhibits phases to the earth, or some slight deviation from the perfect roundness of his disk.
57. The disk of the great and beautiful planet Jupiter, always appears with dark streaks drawn across in a determinate direction. Fig. 19 gives a view of these streaks as observed at Slough with a 20-foot reflector on Sept. 23, 1832; these are, however, by no means the same at all times. Remarkable dark spots also, resembling masses of clouds, are not rare; and from careful and continued observations of these spots, the conclusion has been derived, that Jupiter rotates in 9 hours, 55 minutes, 50 seconds (sidereal time), upon an axis perpendicular to the direction of the streaks. On account of the parallelism of these streaks with Jupiter’s equator, their oft-occurring changes, and, finally, from appearances of the spots, it may be maintained that these streaks belong to Jupiter’s atmosphere, forming tracts in a tolerably serene sky, and are produced by currents similar to our trade winds. They have, nevertheless, a much more permanent and decided character than the clouds in our atmosphere, which may result from the enormous velocity of rotation of the mighty planet. Moreover, that we perceive in the streaks the proportionally darker body of Jupiter is clear, from the well known circumstance that these streaks do not reach to the very edge of the disk, but fade gradually away before they arrive there.
58. Saturn (fig. 20) is surrounded by an attendant of entirely unique and wonderful character; for accompanied as he is by seven moons, he is also surrounded by two broad and flat, though thin rings, concentric with each other and the planet. Both rings lie in the same plane, and are entirely separated from each other by a narrow, and from Saturn by a much broader interspace. The interval between the planet and the inner edge of the inner ring amounts to 18,572 geographical miles, the breadth of the inner ring to 29,820, the interval between the inner and the outer rings to 1556, and the breadth of the outer ring to 18,356, and finally the thickness of each ring to 88 geographical miles. Pl. 8, fig. 20, gives a view of Saturn surrounded by his rings, and with dark streaks on his surface, tolerably similar to those of Jupiter; they are however broader and not so evident, although probably originating in the same cause. The supposition that the double ring of Saturn is a solid and opake mass, is confirmed by the fact that it casts a shadow upon the planet, and is shadowed by it in certain positions with relation to the sun. The parallelism of the streaks with the plane of the ring, makes it probable that the axis of rotation of Saturn is perpendicular to this plane, this supposition also being confirmed by the extended dark spots on the planet. From accurate observations of these spots, the period of rotation has been established at about 10 hours, 29 minutes, 17 seconds.
59. Uranus is too distant for the observation of spots on his surface which might assist in determining his period of rotation. Nevertheless it must be supposed that like Jupiter and Saturn, Uranus possesses a very short term of rotation, since Madler has plainly discovered a flattening of the planet’s disk, which by measurements instituted has been found to be quite considerable. Consequently by reason of this considerable flattening, the velocity of rotation of Uranus must be very great.
The Comets, Nebulæ, Groups of Stars
60. Fig. 15, pl. 8, represents the comet of 1819, which, suddenly emerging from the beams of the sun, appeared to Europe, in the beginning of July, of remarkable size. Arago maintained that the light of this comet exhibited traces of polarization, which can only be exhibited by reflected light. This fact speaks strongly for the theory of Olbers, who maintained that the comets are non-luminous bodies, only rendered visible by the reflected light of the sun. Comets consist of a usually spherical nebulous envelope, with a somewhat brighter nucleus, although occasionally without the latter. Sometimes the nucleus is of great size; thus, for instance, that of the great comet of 1811 had a diameter of at least 560,000 geographical miles. In general the nebulosity does not entirely surround the nucleus, but exists as a spherical hull, elongated on the side of the tail, so that the tail appears as a continuation of the nebulosity. It seems besides, that this nebulous envelope constitutes the chief peculiarity of comets, as many of these wandering stars are seen, some without tails, some without nucleus, none however without the nebulosity. The tail is generally found on the side f opposite to the sun; at times, however, it deviates from this direction, which may be a consequence of the resistance of the ether in which the comet moves. The length of the tail is very various. Thus for instance the length of the tail of the great comet of 1811 (pl. 8, fig. 17) amounted on Oct. 12 to above 88 millions of geographical miles. The tails also become broader towards their extremity, and are often divided longitudinally in their middle by a dark line, so that it seems as if the tail were double. This was plainly perceived on the 10th of Sept. 1811 in the great comet, as shown in fig. 16. The sun undoubtedly produces the tail, as this is always first visible when the comet approaches the sun, becomes larger as the approximation increases, and again diminishes with the gradual increase of distance between the two bodies. Consequently the tails appear, for the most part, to consist of very thin vapor developed by the heat of the sun from the nucleus of the comet. The alterations arising from this cause, which, according to numerous observations, must often be enormous, and may take place even within a few days, doubtless produce the changes observed in the size, shape, and brilliancy of comets. When a comet becomes visible to the naked eye, it is generally seen but a short time, and has a very different course in the heavens from the planets, though it follows the usual daily motion of the heavens. Formerly, on account of the rarity of comets, their remarkable appearance, and their course, it was supposed that they were not true heavenly bodies. Newton, however, first showed that they, like the planets, are heavenly bodies belonging to our solar system. Like the planets, they describe, according to the same laws, orbits around the sun. The eccentricity of their orbits is very great. It is now also known that telescopic comets, or those only visible to the eye when assisted by a good telescope, occur in far greater numbers than others, and that multitudes of them are probably always present in the space belonging to our solar system.
There are thus far, only three comets whose return has been calculated several times, and whose orbits are accurately known. The first of these is Halley’s comet. Halley found that the comets of 1456, 1531, 1607, and 1682 were one and the same, which, he predicted, would return in the beginning of 1759. His prediction was nearly fulfilled. It again appeared in 1835, and is next expected in the end of 1911. The period of revolution of this comet, which can approach within 48 millions of miles of the sun, and recede from him 2920 millions of miles, embraces 76 years. The inclination of its orbit is 17° 44′, and its eccentricity is \(\frac{97}{100}\) of the semi-major axis. The motion of this comet is retrograde.
The second comet, discovered by Pons in Nov. 26, 1818, is the direct comet of Encke, with the very short period of 3\(\frac{1}{2}\) years. Encke found that it had been already observed in 1786, 1795, and 1805, that its perihelion distance was 26 millions of miles, its aphelion 340 millions, the inclination of its orbit 13°, and the eccentricity \(\frac{85}{100}\) of the semi-major axis. The predictions of later reappearances of this comet, whose course is affected by the resistance of the ether (sec. 50), were fulfilled in 1825, 1828.. 1832, &c.
The third, also a direct comet, was discovered by Biela, 28th Feb. 1826, and named after him. This comet revolves in 6f years about the sun. Its aphelion distance amounts to 508 millions of geographical miles, while its perihelion comes very near the earth’s orbit. This, as is well known, is the comet which in 1832 passed near the earth, and on that account excited universal apprehension. The inclination of its orbit amounts to 13°, and the eccentricity to \(\frac{74}{100}\) of the semi-major axis.
Besides these three comets, there are some others recently discovered, whose periods have been found with great accuracy. Their return in the calculated time must, however, be determined by experience. Of these, the best known is the one discovered in the constellation of the Fly, by Olbers, March 6, 1815, and named after him. The motion of this comet is direct. It approaches to within 100 millions of geographical miles of the sun, and recedes to a distance of 2840 millions. The inclination of its orbit amounts to 44°, its eccentricity to \(\frac{93}{100}\) of the semi-major axis, and its period to a little more than 74 years. Its re-appearance may consequently be looked for about the year 1889.
While in earlier times comets were looked upon as harbingers of misfortune, or as indicative of Divine wrath, more recently the fear has been excited, lest, on account of their great number, and the various positions of their orbits with respect to that of the earth, a comet may at some time or other come in contact with the earth. This fear, however, Olbers, more than 40 years ago, by his copious investigations of the numbers and orbits of comets, sought to remove as far as possible.
In conclusion, it remains to say that very recently, two more great and beautiful comets, namely, those of February, 1843, and May, 1845, haw appeared and been carefully examined.
61. We turn now to several interesting objects of the starry heavens, which are represented on the left and right sides of pl. 8. Fig. 1 is a crowded group of stars of irregular outline, seen in the constellation of Hercules, under a right ascension 248° 45′, and north declination of 36° 48′. Stars of the 10th to the 15th magnitude stand very close together, the diameter of the whole amounting to about 8 minutes.
We have already referred in general terms, in sections 15 and 16, to the groups or clusters of stars, as also to nebulous stars and nebulae. Fig. 2 gives a representation of a beautiful circular group of stars in Aquarius, resolvable near the centre by a good telescope, and seen under 321° 15′ right ascension, and 1° 34′ south declination. Towards the centre it is very clear and uniformly brilliant, although the stars do not stand thicker here than towards the border; the central brightest part amounts to six seconds of diameter.
Many groups of stars are fan-shaped, as in fig. 3 or fig. 4, which latter occurs in the constellation Cancer. The round nebula (fig. 5) is found in Ursa Major. In Gemini, under right ascension 109\(\frac{1}{2}\)°, and north declination 26° 26′, there is a nebula (fig. 6) whose central star has a great, irregularly oval atmosphere. In Leo Major, 167\(\frac{3}{4}\)° right ascension, and 41\(\frac{1}{2}\)° north declination, may be perceived a star (fig. 7) in the middle of an elliptical nebula, very much pointed at the ends. Two other nebulas (figs. 8 and 9) occur in Monoceros; one of them (fig. 9) of right ascension 97\(\frac{1}{2}\)°, and south declination 8° 53′, is a star of the 12th magnitude, with a luminous nebulous train of about one minute in length, not unlike the tail of a comet.
Two and even more stars are often seen enveloped in one nebulous mass, evidently belonging to them both, standing in the two foci or the two vertices of the elliptical nebula. One of this kind is to be met in Canes Venatici, under right ascension 192\(\frac{3}{4}\)°, and north declination 35° 47′, where the two stars (fig. 10) are of the 10th magnitude; in Sagittarius there is a bright elliptical nebula (fig. 11), with a star in each of the foci. In the constellation Auriga, a nebula with three stars is observable, which is round (fig. 12) according to some, but triangular (fig. 13) according to others. Fig. 14 represents the great nebula in Andromeda, figured also from another view on pl. 13, fig. 10.
The Aurora. Mock Suns and Mock Moons.
62. Although the phenomena now to be referred to, belong more properly to the department of meteorology, to which a special section will be devoted, yet they cannot remain entirely unnoticed under the present head. The Aurora, improperly called northern light, as it appears at the south pole as well as the north, is the name of a luminous, often circular meteor, which sometimes appears in the vicinity of the magnetic pole of the earth, and shines with an indescribable hue. It is only recently that astronomers have included the Aurora or polar light within the circle of their observations, and have found in almost every case, that simultaneously with the appearance of a northern light, there are certain phenomena about the south pole, sometimes consisting only of unusual disturbance of the magnetic needle. The eighteenth century was very prolific of northern lights, particularly the middle part of it; since 1820 they have also become much more frequent. Pl. 14, fig. 57, is a view of the remarkable Aurora Borealis which was seen at Christiania in Norway, at 6 o’clock in the evening of January 7, 1831. Fig. 58 represents an Aurora Australis or south polar light.
The mock suns and mock moons, or parhelia and parselenia, are a result of a peculiar reflection of the light of the sun, of the moon, and even of the brighter planets and fixed stars, upon particles of condensed vapor or ice crystals. When these halos are very much complicated about the sun and moon, they appear as if composed of many circles intersecting each other, of which one is generally horizontal, encircling the whole heavens. It is in this case that they form mock suns and mock moons. Generally, only two or four are seen; Hevelius, however, in 1660, saw six at once; sometimes they have comet-like trains. Pl. 14, fig. 59, exhibits a view of two such mock suns.
The Shooting Stars
63. The shooting stars have been long and universally known, but it is only in recent times that their true character, their peculiarities, and the various circumstances under which they are perceived, have been matters of observation to astronomers and meteorologists. The periodical and abundant return of the shooting stars towards the middle of August and November, has in many places been diligently observed and investigated. We need only mention the efforts of Benzenberg, Brandes, Olbers, Bessel, Erman, Boguslawski, Quetelet, Feldt, Herrick, and Olmstead, to ascertain their direction, their height above the earth, and their velocity. The reasons for the now generally received hypothesis (of Alexander von Humboldt) are well known; his theory being that these luminous appearances are caused by innumerable small bodies revolving about the sun, which become visible by their combustion when entering the atmosphere of our earth. There are yet many difficulties in the way of the establishment of this theory, as also of the supposition of Biot, that these falling stars are the same bodies which, seen at a distance, form the zodiacal light.
Benzenberg and Brandes divide all shooting stars into three classes: 1, of the first and second magnitudes, similar to balls of fire, in which may be distinguished a ball with a luminous train; 2, of the first and second magnitudes, without the ball, and with a luminous path; 3, from the third to the sixth magnitudes, the last being telescopic, and only visible through a comet seeker.
The number of shooting stars is incredibly great. Humboldt and Bonpland observed a magnificent fall of these bodies in 1799, and Brandes counted during one night, in a fifth part of the horizon, 480 shooting stars, from which he estimated the whole number, during the same time, at some thousands. Every one is familiar with the extraordinary showers which have appeared in America at various times. Benzenberg estimates the mean number appearing every night to be 30, 50, and even more. The train appearing behind the greater shooting stars deserves particular attention. Brandes has accurately observed and described the remarkable appearances presented by the last.
The height of these bodies is very various; some of them seem tolerably near the earth, while others are beyond the outer layers of the atmosphere, assuming this at 80 to 120 geographical miles from the surface of the earth.
The velocity of these meteors amounts, according to calculation based on observation, to between 16 and 32 miles in a second, thus reaching sometimes twice the velocity of the motion of our earth in space. Olbers has first shown how the shape of their orbit can be determined.
With regard to the substance of which the shooting stars are composed, nothing satisfactory is known.
The Antipodes of our Earth; the Habitableness of the Worlds of the Solar System
64. The inhabitants of our earth may be considered, astronomically, under two points of view, namely, in respect to the degrees of latitude and longitude under which they live, and also in respect to the direction in which their shadow falls. By Antipodes is meant the inhabitants of that place on the earth’s surface lying the distance of a complete diameter of the globe from some other place, as, for instance, Leipzig. The antipodes have an opposite geographical latitude, and a geographical longitude differing by 180 degrees; consequently, with the exception of those near the equator, an opposite time of year, and a time of day differing by 12 hours. Leipzig, for instance, has a north latitude of 51°, 20′, 20″, and a longitude 30°, 1′, 52″ east of Ferro; the antipodes of Leipzig, therefore, must dwell on a part of the earth’s surface having a south latitude of 51°, 20′, 20″, and a longitude of 210°, 1′, 52″ east of Ferro. This point, however, lies in the great southern ocean, and, consequently, there are no proper antipodes to Leipzig.
Antæci (αυτιοικοι) are the inhabitants of two places on the earth’s surface, lying under the same meridian and at the same distance from the equator, but on opposite hemispheres. These have noon at the same time, but of course opposite seasons. At the two poles the antæci are also antipodes.
Periaeci (πεζιοικοι) are those persons, who, living under the same latitude, differ in longitude by 180°. They have consequently the same seasons, but their days differ by twelve hours. At the equator, antipodes and periæci are synonymous.
65. Heteroscii (ἑτεζοκοι), or one-shadowed, are those inhabitants of the earth whose shadows among themselves always fall in the same direction; in an opposite direction, however, to the inhabitants of the opposite hemisphere. Consequently, the inhabitants of the temperate zones are one-shadowed; the shadows in the north temperate zone falling north, those in the south temperate zone, south.
The inhabitants of the frigid zones acquire the name of Periscii (πεζι-σικοι), at the time during which the sun remaining above their horizon causes their shadows to move in a circle around them in the space of 24 hours.
Amphiscii (αμφ-σικοι), or double-shadowed, are those inhabitants of the tropics who for one half of the year have their shadows directed towards the south, and for the other half towards the north. The cause of this lies in the fact of the latitude being less than the obliquity of the ecliptic. At any place whose latitude is, for instance, 17° north or south, a body will cast no shadow at all at noon of the day, when the declination of the sun is likewise 17° north or south. For this reason the Amphiscii are then termed Ascii (α-σικοι), or shadowless. The inhabitants of the equatorial line itself will be shadowless on the 21st of March and 23d of September, since on these days the sun stands in the celestial equator. It has, consequently, then no declination, and the inhabitants of the line have no latitude.
66. It is not absolutely impossible that the sun may be habitable, as the black places which are seen in the middle of the sun’s spots represent, perhaps, not the true nucleus of the sun, but only an obscure atmosphere similar to our own. The inhabitants of the sun, therefore, undazzled by the piercing light of the external solar surface or photosphere, and protected from its excessive heat, may live, ignorant, however, of the alternation of day and night. Neither can they know anything of seasons, since they are surrounded on all sides, and at all times, by the sources of heat and light. They can thus know nothing of the existence of the planets, moons, and comets; and can perceive the starry heavens in their beauty only through the openings which those violent agitations in the sun’s photosphere sometimes produce.
67. Although Mercury receives an illumination from the sun almost seven times greater than that of our earth, the heat thus produced may be very greatly tempered by the numerous high mountains with their long shadows, the rapid alternation of the seasons, and the probably very rare atmosphere. In this manner an alleviation of temperature may result, which will without difficulty admit of this planet’s being habitable.
Certain phenomena must take place in the climate and seasons of Venus which hardly admit of a comparison with ours. A day of Venus is very nearly equal to one of the earth, but it is very different with respect to the seasons, if we assume, as established, that the axis about which Venus rotates daily is inclined to its orbit at an angle of nearly 72°, and that thus the obliquity of her ecliptic is nearly three times that of the earth. It is well known that the seasons are determined by the obliquity of the ecliptic, and that, consequently, a much greater obliquity than that of our earth must necessarily involve a corresponding influence upon the temperature, and especially upon the alternation of the seasons: it may, therefore, be assumed for Venus, that when the given circumstances take place, the torrid zone, whose inhabitants have the sun in their zenith, must cover a space of 144 degrees in breadth, while the breadth of this zone on our earth is but 47°. The frigid zone will lie at the two poles, extending 18 degrees towards the equator. The inhabitants of this zone will never see the sun in their zenith. In the temperate zone, occupying a space of 54 degrees from the frigid zone towards the equator, the inhabitants will not see the sun at all during one part of the year, and during another will have him in their zenith, thus resembling the inhabitants of both frigid and torrid zones on our earth. Hence it happens that the dwellers on Venus must experience such sudden alternations of season and climate as our imagination can hardly comprehend.
68. With respect to our moon, the curious arrangement of day and night, the want of an atmosphere similar to ours, of great bodies of water, and of seasons, as also the universal sterility and drought which seem to reign upon its surface, must undoubtedly exert an influence upon vegetable as well as animal life, of which we can have no adequate idea. The inhabitants of the moon, therefore, should such exist, must be very different from those of the earth. Even the view of the starry firmament from the moon must be very peculiar, since to its inhabitants the earth never sets. They who live in the centre of her visible disk always have the earth in the zenith, while those living on the border see us in their horizon. Sun. planets, and all other celestial objects, complete their paths in 29\(\frac{1}{2}\) days, and thus rise and set, to the moon, every 14–15 days. The difference of seasons vanishes almost entirely on the moon, on account of the slight inclination of the equator to its orbit ; and while the inhabitants of her equator have the sun always in the zenith, those of the poles see him always in the horizon. In the former part, therefore, there reigns an eternal summer; in the latter, an eternal winter; while intermediate between the two. a perpetual spring prevails. Days and nights are ever almost equal in length.
69. The physical condition of Mars most nearly resembles that of the earth; it is impossible, however, to offer any plausible hypothesis with regard to the asteroids, Vesta, Iris, Astræa, Juno, Ceres, and Pallas, as their distance and diminutive size conceal from us the peculiarities of their surface.
70. Since the various alternations of Jupiter follow each other with great rapidity, his hypothetical inhabitants must possess great quickness of mind and body. If their size bears any proportion to that of the planet, their height must be about 70 feet.
The inhabitants of Saturn, if any, must be entirely different from ourselves, and we have no cause to envy them. The nights of Saturn, as also the winters, last 15 years; there are total eclipses of the sun which last whole years; the sun appears ninety times less to them than to us; and, for years, total darkness and general torpidity, in all probability, reign supreme.
Whether the ring and the seven moons of Saturn, and whether Uranus and Neptune with their moons, are habitable, are questions which must be left unanswered, as these planets, although little smaller than Saturn, are so remote as to render it impossible for us to ascertain the peculiarities of their physical condition by means of our telescopes.
As it is hardly supposable that all the planets and moons revolve about the sun as uninhabited worlds, and that only the earth has the prerogative of being peopled with any kind of created beings, so it seems not impossible, yea, rather entirely suited to the omnipotence of the Deity, to assume a certain habitableness of the comets. Shall these heavenly bodies, which are by far the most numerous of all the worlds belonging to our solar system, and in proportion to which the numbers of primary and secondary planets vanish away—shall these be entirely uninhabited, simply because man cannot comprehend of what sort the beings dwelling on the comets must be? In fact, it is a sentiment completely recognising the all-wise beneficence of the Creator, to presuppose that, upon those worlds wandering through such an immense extent of the heavens, certain beings may exist, as comfortable and happy as man, who so complacently considers himself as lord of the earth.
The Calendar in General; the Greek, Julian, Gregorian, Russo-Grecian, Jewish, Turkish, and French Republican Calendars in particular
71. The Calendar belongs, from its nature and particular application, to the department of Chronology. Chronology, however, forms a part of astronomy, and, indeed, is a part of the greatest importance and most material value to the sciences, particularly the historical and political. For this reason it will not be superfluous to present here the most important features of the different calendars.
72. Calendar means partly the division of time employed by any people into definite years, months, &c, and partly the register of single days answering to a certain year of such a division. The word calendar is derived from the Latin calendar (καλεω, Lat. calo, to call), by which name the Romans indicated the first day of every month, whose name and new moon were proclaimed by the priests, the calendar of any given year containing not only the religious and political festivals, but also the most important celestial events of that year. Among the latter are to be reckoned especially, the rise and setting of the sun and moon, the length of days and nights, the quarters of the moon, the eclipses of the sun and moon, the appearance of the planets, &c. We distinguish also, not only the calendars of different nations, but also special calendars, according to purport or object. Thus, for instance, we have astronomical, civic, centennial, economical, people, and states’ calendars. We shall, now hurry over the calendars of the most important nations in order.
Calendar of the Ancient Greeks
73. The ancient Greeks assumed a lunar year of 354, later of 360 days, or 12 months of 30 days each, which they then sought to accommodate to the true solar year by intercalations. In honor of the Olympic games, the beginning of the year was placed at the first new moon after the summer solstice. Nevertheless, this did not always fall in July, as the Olympiads themselves consisted sometimes of 49, sometimes of 50 months. This Greek calendar was as complicated as the Macedono-Grecian calendar, introduced at a later period by Philip of Macedon, which commenced its year at the autumnal equinox, and which was employed for the names of the months, but not in their order, by the Greeks, Phoenicians, Babylonians, Medes, &c. The months of 30 days were called full; those of 29 days deficient; and each of these fell into three decades. By the gradual introduction of the Roman calendar among the nations subjected to that power, the Grecian fell into disuse.
Calendar of the Romans; the Julian Calendar
74. The Roman calendar, improved by Numa Pompilius, was based on a lunar year, having one more day than a solar year. The first day of every month (the new moon) was called the calend, and besides this, two others were distinguished, the 18th before every new moon the Ide, and the 9th before the Ide the None. According to the reckoning of Numa, four months (Martius, Mai us, Quintilis, and October) contained 31 days, and the rest 29 days, except February with 28, and the Macedonian month which was intercalated every two years with 22–23. There were therefore nones of seven and of nine days ; with later arrangements the Ides also happened differently. The intermediate days were counted backwards from the Ides of the same, or the calends of the next month, as also from the nones of the same month. The Romans had besides periods of nine days, called nundinæ, which were indicated by the letters A to I. The dies fasti and nefasti were days of good and bad omen. Through the irregularity of distribution, and the then low state of astronomical science, it came to pass that about 46 years b.c. the Roman calendar varied about 59 days from the true day (that is, from the true place of the sun in the ecliptic). This induced Julius Caesar, by the advice of the Alexandrian mathematician, Sosigenes, to adopt the solar year of 365 days, 6 hours, and so arrange the calendar that every year divisible without remainder by 4, should consist of 366 days, the rest consisting of 365. With respect to the subdivisions of the calendar, Julius Caesar retained the old terms of calends, nones, and ides. This calendar is called the Julian.
Gregorian Calendar
75. The Christians retained the astronomical arrangement of the Julian calendar in general, but established weeks of several days; January was the first month, December the last: January, March, May, July, August, October, and December, had 31 days, while April, June, September, and November, had 30. February had generally 28 days, except during the intercalary or leap year, when it had 29. At a later period, however, the length of the year was altered. Julius Caesar had originally assumed too great a length for the year. This required, even in the time of Augustus, a correction of three days, and in 1581 the error had again amounted to ten days. The then reigning pope decreed on the 24th of February, 1581, an improvement of the calendar, by which ten days should be omitted from October of that year (counting 4, 10, 15 October), and in four centuries three leap years should be omitted, by which the years 1700, 1800, 1900, 2100, &c., were not leap years. This Gregorian calendar was soon introduced into all Catholic countries, while the Protestants retained the old system until 1699. In the year 1700, in February of the new improved calendar of the German Protestants, ten days were omitted, so that March 1st came immediately after February 18th. With respect to Easter, which in the Gregorian calendar of the Catholics was counted after the Epact, the Protestants assumed a purely astronomical mode of calculation, so that this always came on the Sunday after the first full moon succeeding the vernal equinox (thus between March 22 and April 25). This improved calendar agreed for the most part with the Gregorian, but with respect to the different determinations of Easter, cases soon occurred in which one calculation made Saturday, and the other Sunday, the day which determined the celebration of Easter on the Sunday following. According to the latter calculation, therefore, this festival would happen eight days later than as determined by the former, which produced great confusion among those Catholics and Protestants living near each other. When, in 1778, this was about occurring, Frederick II. of Prussia succeeded in persuading the Protestants of Germany to adopt the determination of Easter by the Epact. To this arrangement the other Protestant states of Europe have also conformed.
It will be necessary to add a few explanations of certain expressions which are connected with the determination of single days and festivals in our calendar. The determination of Sundays and week days depends upon the Sunday or Dominical Letter, and the Solar Cycle. The Sunday letter is that which falls upon the first Sunday, when we call the first day of the year A, and count from A to G. Should the year be leap year, count the Sundays after February 24th one further. It is necessary to know these letters to understand the construction of the perpetual calendar.
The number of years after which the same week days fall upon the same date again, is determined by the solar cycle. Were there no leap years, then, as the date annually advances one on the days of the week, the same date would fall every seven years upon the same day of the week; since, however, every fourth year is leap year this coincidence takes place every 28 years, which form one solar cycle, the series beginning the ninth year b.c.; thus, in 1847, the solar cycle is VIII., that is, it is the eighth year of a sun cycle in the nineteenth century.
The Lunar Cycle, the golden number, and the Epacts, serve to determine the phases of the moon, and occurrence of Easter. The lunar cycle is the series of years after which the new and full moons again fall upon the same day of the year. This cycle amounts to 19 years of 365\(\frac{1}{4}\) days, and the number of any year indicating its place in the cycle, is called the golden number. This cycle was discovered by Meton, 430 b.c., and the golden number is the remainder after adding one to the number of years, and dividing by 19. The quotient indicates the number of lunar cycles which have elapsed since a.d. up to the given time. Should the golden number be one, then the new moon falls on Jan. 1. For the determination of the new moon of any other years, the Epacts are employed, or the number which, for every year, determines the age of the moon on New Year’s day, or gives the number of days by which the last new moon of the previous year preceded New Year’s day. Should the new moon fall on Jan. 1, then the Epact = 0.
As the lunar year is 10 days, 15 hours, 11 minutes, 25 seconds, or, in round numbers, 11 days shorter than the solar, it follows that the Epacts increase annually by 11; so that if, in one year, the Epact was 23, in the following it would be 3, as the series commences with 1 after 30. The passage from the last year of a lunar cycle to the first of the following, amounts, not to 11, but to 12 days, and is called the leap of the Epacts. This intercalary day is necessary, from the fact that the lunar year is not quite 11 days shorter than the solar year. For the year 1847 the golden number is 5, and the Epact 14. Knowing the Epacts, it is possible in a perpetual calendar to determine immediately every day upon which new moon falls. Thus, for the Epact 14, of 1847, the first new moon falls on the 16th of January; nevertheless, small errors cannot always be avoided, as, for instance, is the case in the year mentioned, when the first new moon actually occurs early on the 17th January, at 1 hour, 34 minutes. After the occurrence of the new moon, we can readily determine the remaining phases of the moon.
Russo-Grecian Calendar
76. The calendar of the Russians and Greeks has, in respect to the months, weeks, main festivals, &c., the same arrangement as the Gregorian calendar; nevertheless, these nations have retained the Julian in its essential features, that is, with respect to Easter and the festivals dependent upon it. They are, therefore, about. 13 days behind the Gregorian date now, and will, in 1900: be 14 days; so that in the present century, for example, when they have March 1st according to their calendar, it will be March 13th according to the Gregorian. The Greeks and Russians have, thus, the old style reckoning; the other Christians, the new style.
Jewish Calendar
77. The Jewish years are lunar years, counted from Oct. 7th of 3761 b.c. The Jews have, according to the improvement of Rabbi Hillel Hanaffi, a cycle of 19 years, among which 12 are common, and 7 intercalary years. One of the former has 354 days, 21 hours, 48 minutes; one of the latter, 383 days, 21 hours, 48 minutes. To satisfy the priestly arrangement there are six different years, namely, three common years of 12 months each, the short year having 353, the mean year 354, and the long year 355 days; and three intercalary or leap years, of 13 months each, the short year having 383, the mean 384, and the long 385 days. The beginning of the year can fall neither on Sunday, Wednesday, nor Friday. The months of the civil year are in order as follows: Tischri, Machesvan, Kislev, Tebeth, Schewat, Adar, W’Adar (intercalary month), Nisan, Jjar, Sivan, Thamuz, Ab, and Elul. The religious year begins with the month Nisan, in which the principal festival, the Passover (Easter), falls, and, indeed, always on the 15th Nisan. This Passover, which can never fall on a Monday, Wednesday, or Friday, is of the greatest importance in the arrangement of the Jewish calendar, and generally occurs in our Passion week. In conclusion, it may be stated, that our Saturday is kept under the name of Sabbath (day of rest) just as Sunday is with us.
Turkish Calendar
78. The Turks and almost all adherents of Mohammedanism count their years from Hedschra, or Hegira (July 15, 622 a.d.). They have a cycle of 30 years, each consisting of 354 days, except 11, which are leap years of 355 days. Their year, whose mean length amounts to 354 days, 8 hours, 48 minutes, is divided into 12 months of 30 and 29 days: Moharem, Sepher, Rabi el Auwal, Rabi el Achar, Dsjommada el Auwal, Dsjommada el Achar, Radsjeb, Schaban, Ramauan, Schauwal, Dsulkade, and Sulhadsje. In the leap year, the last month, Sulhadsje, instead of 29, has 30 days, the latter being the intercalary day. The festivals of the Turkish calendar occur unchangeably on the same day of the month.
Calendar of the French Republic
79. By a decree of the French National Convention of Oct. 5th, 1793, a new reckoning of time was adopted, dating from September 22d, 1792, on which day, previously fixed upon, the establishment of the Republic was decreed. As this was also the date of the equinox (at 9h 18′ 13″ of the morning) there was an allusion given to equality both of days and rights. The following years were also to begin with the midnight preceding the true autumnal equinox. This new French year was divided into 12 months of 30 days, and to complete the number of days, five, or in leap year six supplementary days (jours complementaires), were added. Instead of weeks, the months were divided into three decades of 10 days each. These ten days were called Primidi, Duodi, Tridi, Quartidi, Quintidi, Sextidi, Septidi, Octidi, Nonidi, and Decadi. The nomenclature of the months was derived from the characteristics of the seasons, as follows:—
For Autumn: Vendemiaire, or vintage month (October); Brumaire, or cloud month (November); Frimaire, or frost month (December).
For Winter: Nivôse, or snow month (January); Ventose, or wind month (February); Pluviose, or rain month (March).
For Spring: Germinal, or growth month (April) ; Floréal, or bloom month (May); Prairéal, or meadow month (June).
For Summer: Messidor, or harvest month (July); Thermidor, or heat month (August); Fructidor, or fruit month (September).
The additional days are attached to this last month, and have the following appellations:—1st, Fête du genie; 2d, Fête du travail; 3d, Fête des actions; 4th, Fête des recompenses; 5th, Fête de l’opinion.
In addition to what has already been said, every day of the year had its especial name, which, instead of being. taken from some saint, was derived from objects of agriculture appropriate to the time on which the days fell. This calendar, however, lasted only 12 years, for Napoleon abolished it by a Senate decree of September 9, 1805.
Astronomical Instruments; Observatories
80. Astronomical instruments embrace all the apparatus which the practical astronomer needs in his observations of celestial phenomena, to impart to them that accuracy and certainty so necessary as the basis of delicate calculations, as also to find objects in the heavens invisible to the naked eye. Astronomical instruments have two purposes: the one is to afford a clear understanding of those objects and phenomena of the heavens, which, on account of their distance or minuteness, are either imperfectly or not at all visible to the naked eye; the other purpose is the accurate measurement of various angles and spaces. The following may therefore be considered as the most important astronomical instruments:—Transit Instrument, Equatorial, Refractor, Meridian Circle, Universal Instrument, Comet Seeker, Heliometer, Simple Circle, Theodolite, Multiplication Circle, Reflecting Sextant, Barometer, Thermometer, Pendulum Clock, Chronometer, &c. Of the more ancient instruments, only the Zenith Sector and Mural Quadrant are retained at the present day; all the rest, as, for example, the Octants, Quadrants, Telescopes without tubes, &c., are consigned to deserved oblivion.
The following are the names of some artists distinguished for the excellence of the astronomical instruments constructed by them. Those marked + are deceased. Baumann (in Stuttgart); Breithaupt (in Cassel); Cauchoix (in Paris); Dollond+ (in London); Douve+ (in Berlin); Emery+, Ertel (in Munich); Fraunhofer+ (in Munich); W. Herschel+, Jürgensen (in Copenhagen); Kessels (in Altona); Lerebours (in Paris); Merz and Mahler (in Munich); Oertling and Pistor (in Berlin); Plössl (in Vienna); Ramsden+ (in London); Repsold, sen.,+ and Repsold Bro’s (in Hamburg); Reichenbach+ (in Munich); Lord Rosse (in Ireland); Troughton+ (in London); Voigtländer (in Vienna); and others.

The Telescope; its Different Constructions
The Dorpat Refractor
81. The Telescope is that optical instrument which represents distant objects more distinctly and of larger size than they appear to the naked eye. There are two principal kinds of telescopes, dioptric or refractors, and catoptric (or more properly catadioptric) or reflectors. In refractors, observations are conducted by means of glasses alone, as, for example, the eye glass and object glass; in reflectors a concave mirror is used instead of the object glass. Both were invented in the sixteenth and seventeenth centuries; the refractor in 1590, by Jansen of Middleburg, and the reflector in 1644, by Mersenne.
Refractors consist of a cylindrical tube at whose two extremities are placed the lenses employed. The lens receiving the rays of light from the object, is called the object glass or objective. The one through which the image produced is seen by the eye is called the eye-glass or ocular. Eye-glasses are simple when but one lens is used, compound when several lenses are combined together. Besides the magnifying power of the telescope, reference must be had to the diameter of the field of vision, the illumination or amount of light, and the degree of distinctness of vision.
There are three kinds of refracting telescopes; the astronomical, invented by Kepler; the terrestrial, invented by De Rheita, 1665 ; and the Galilean. The astronomical telescope is formed by the combination of two convex lenses ; the one, the eye-glass, can be made to approach to or recede from the object glass. This form of telescope, although it represents objects inverted, exhibits them very clearly and much magnified; having also a large field, it is on this account principally used by astronomers.
The second kind, or the terrestrial telescope, is a combination of four convex lenses; three of them, fixed immovably in one tube, can be made to vary their position with respect to the fourth—the object glass. This telescope, which exhibits objects erect, may be considered as a combination of two astronomical telescopes, of which the one represents the inverted image of the other again inverted, consequently actually erect. Nevertheless, it is more advantageous to furnish the terrestrial telescope with four eye-glasses, as is generally done. The eye-glass nearest the eye thus obtains (as also happens in astronomical telescopes) a second eye-glass viz. the so called field glass, for the purpose of enlarging the field of vision.
The Galilean telescope is the simplest of all, consisting of but two lenses—a convex object glass, and a concave eye-glass ; this represents objects erect. It has. however, the inconvenience of possessing a very small field of vision, especially when the eye is not exceedingly near the eye-glass.
The common telescopes, however, do not exhibit any very great degree of clearness of vision, as all images produced by them are surrounded by a colored border, and a considerable magnifying power can only be obtained with a length of 5 or 6 feet. Dollond remedied this defect in 1757 by his achromatic (colorless) object glasses. An achromatic object glass consists of two highly polished lenses, combined so as to be everywhere in absolute contact, the one convex, made of crown glass, the other concave, of flint glass. The two kinds of glass have different refractive powers, so that chromatic aberration is reduced almost to a minimum. Telescopes with such object glasses, and of a moderate length, afford with a considerable magnifying power, and great brightness and distinctness, images almost entirely without colored borders. Very large instruments of this kind are known pre-eminently as refractors. The preparation of the glass required, so as to be everywhere uniform and without bubbles and streaks, presented great difficulties, until they were surmounted by Fraunhofer and Uzschneider.
On account of the differences in eyes, and the varying distances of objects, a special adjustment is required for the eye-piece. In small telescopes this is done by moving the tube in or out with the hand alone; in larger instruments a screw adjustment is necessary, by which the eye-piece (ocular) can be moved almost insensibly. The larger telescopes are set up either on a three-legged frame or upon a pyramidal support, and their motions are either horizontal and vertical, or for astronomical purposes parallactic, i. e. applicable to any direction.
As an illustration of the mode of constructing and setting up a great telescope, we have selected the giant achromatic refractor constructed by Fraunhofer for the observatory of Dorpat. The instrument arrived there November 10th, 1824, and the first glance was directed by Struve, six days afterwards, towards the moon and some double stars. The principal parts of the instrument (pl. 15, fig. 2) are—1, the stand A, A, A; 2, the axes F and I, with their circles d and k; 3, the telescope B, B; 4, the counter-poises E, E′, K, M, H; 5, the clock-work, e, f, g, with the weights. The stand is parallactic; upon it rests the hour axis F, parallel to the polar axis, with its hour circle, d, at the lower end. A second axis, I, stands perpendicular to the first, and consequently in a rotation of the instrument about the latter, describes the plane of the equator. At one end of this second axis is the declination circle, k; at the other, the bed of the wooden tube, B, B, of the telescope, with brass caps at the two ends for the lenses, and the finder, D, D, at the upper side. The counterpoises are five; two, E and E′ on the telescope, to balance the greater weight of the anterior half of the instrument; two, M and K, in the direction of the declination axis; and one, H, to diminish the friction of the hour axis. The clockwork, e, f, g, lies on the left side of the hour circle, d, and acts upon an endless screw which catches in it, and even without the clock-work, may be employed to produce a gentle motion about the hour circle. A second micrometer screw, i, is attached to the declination circle, k, to produce the adjustment in the declination. In a perpendicular position of the telescope, the height of the whole instrument amounts to 16 Paris feet, and the weight to about 4000 Russian pounds. The steel hour axis, 39 inches in length, carries the hour circle of 13 inches diameter, with a graduation on silver on its lower face; each of the two verniers reads to within 4 seconds of time. The declination circle is 20 inches in diameter, and its motion is regulated by a clamp and micrometer screw. The circle itself has a graduation on silver, and the vernier reads to 10″. The length of the telescope is 13\(\frac{7}{12}\) Paris feet, with a diameter of 10 inches at the upper end, and 7\(\frac{3}{4}\) at the lower. The object glass has a free aperture of 9 inches, and a focal length of 160. The four free oculars of 1420, 210, 320, and 480 magnifying power, as also the various micrometer apparatus with 14 oculars, can be screwed into the end of the draw tube. The aperture of the objective of 30 inch focus, belonging to the brass finder, amounts to 29 Paris lines. This finder has two oculars of 18 and 26 magnifying power. The clock-work intended to give to the telescope a motion on its hour axis, uniform with that of the fixed stars, and represented on a larger scale fig. 20, consists of two principal parts; the clock proper and the wheelwork connecting this with the hour circle. Both are fastened to the bearing piece at the lower end of the hour axis. This wheel consists of an axis to which are attached the two wheels d and e; on d the disk f (the latter is omitted on the figure) is screwed; a smaller disk, g, is attached anteriorly by the screw h. An endless thread with the weights runs over f and g. At i is seen the spring and trigger catching in the teeth of the disk g; d is in connexion with the little wheel k; l and m are apertures. The clock drives an axle, n, with a double-motioned endless screw, working in the wheel, e. The motion of the clock is regulated by a centrifugal balance wheel which is connected with the weights by means of three wheels and pinions; p and q are cog-wheels, r a crown wheel acting on the pinion of the perpendicular axis t. The centrifugal balance wheel works within the box u; the parts, w, x, y, z, serve to regulate the motion of the clock, which, as well as that of the friction weight, continues to move more than an hour. Both the clock and the friction weight may be removed without disturbing the motion of the telescope. The micrometer arrangements inside the telescope are adjusted with great accuracy, but their enumeration and explanation here would carry us too far out of our way.
The value of this great refractor consists in its optical completeness, in the great accuracy of its adjustments, in the regularity of rotation about the hour axis by means of the clock, as well as in the perfectly unalterable micrometrical apparatus. In defining power and intensity of illumination, this refractor leaves all known reflecting telescopes far behind. Struve saw the multiple star τ Orion certainly 16-foid, while Schroter with his 25 foot refractor only saw it 12-fold; the little companion of the star β Orion (Rigel) was seen through the Dorpat refractor very distinctly just before sunset; and even ω2 Leonis, one of the most difficult double stars, in this instrument, was recognised without any difficulty as a double star. In conclusion, it remains to be mentioned, that this telescope is placed in a building specially arranged for rotation. The cost of the instrument amounted to 10,500 florins ($5000).
More recently the observatory at Pulkowa has received a somewhat larger refractor from Munich, whose object glass has an aperture of 14\(\frac{9}{10}\) Paris inches. The new Berlin observatory also possesses a large refractor of remarkable excellence from this same celebrated manufactory at Munich. The observatories of Cambridge, Washington, and Cincinnati, likewise possess refractors of great power.
When in use, the telescope is directed to the object to be investigated, whose motion is followed by changing the position of the instrument. If the telescope be arranged as in the Dorpat refractor, all the clamps are to be loosened, the object found with the seeker, and the instrument then fixed; upon which, by means of the clock-work, it is moved in such a manner as always to have the object in the field of vision.
The Reflecting Telescope; Herschel’s Giant Telescope
82. Catoptric (catadioptric) telescopes, commonly called reflectors, form the second grand division of these instruments.
The reflector is a telescope which, instead of an object glass, has two mirrors, an objective and a reflecting mirror. New r ton constructed the first reflecting telescope of the form now bearing his name. This consists of a hollow cylinder, so placed upon a frame as to be readily directed to any point of the heavens. The one end of this cylinder is closed by a spherically concave metallic mirror or speculum, whose focus lies in the common axis of the cylinder and mirror. At a little distance from the focus of the speculum is placed a plane mirror inclined to the axis of the cylinder at an angle of 45°. A beam of light impinging upon the concave mirror, is reflected in a cone upon the small plane mirror, and thence into the ocular placed in the side of the instrument and at right angles to it. This arrangement, therefore, represents objects inverted, unless, as in the terrestrial telescope, erecting lenses be placed in the eye-piece. After Newton’s death another form, the Gregorian, with the smaller reflector concave, came into use; this represented objects erect. A third kind, the Cassegrainian, was also introduced. This last has the small anterior reflector convex instead of plane, as in the Newtonian, or of concave, as in the Gregorian; objects are represented in it inverted. Herschel improved the Newtonian telescope by omitting the small reflector, fixing the large concave speculum at a slight angle to the axis. The focus consequently was formed at the anterior edge of the instrument, where it was received by the ocular. The observer sat directly in front of the open tube looking through the ocular.
In this manner Herschel constructed his 20 and 30 foot telescopes; the 20 foot with a speculum of 10 inches diameter. A seven foot reflector finished by Herschel in 1780 was of great excellence; with it he discovered Uranus on the 18th of March, 1781. The magnifying powers were 230, 460, and 930; but to his greater reflector Herschel could apply powers of 500–2000, without overtasking them for strongly illuminated objects. The giant 40 foot telescope completed in 1789, is represented in pl. 15, fig. 1. The tube, DD, constructed of sheet-iron, was 40 feet long, 4 feet 10 inches in diameter, and the whole telescope weighed about 5100 pounds; the great speculum alone weighed 2148 pounds. The magnifying powers of the instrument were, for the planets, 250 and 500; for the fixed stars, 1000–6400. The distinctness of the objects seen is said to have been astonishingly great. The cost of the whole apparatus amounted to about £2000 sterling. During observations with this colossal instrument, Herschel sat at the side of the tube at its upper end, in a frame H, fixed to the ladders, G, G, which accompanied the tube in its movements. He thus looked into the instrument, with his back to the star, and examined this latter directly with the eye-glass. Unfortunately the mirror, during a single damp night, lost its polish, and the whole instrument in a few years after its construction was entirely useless. The figure gives, without the necessity of further explanation, an idea of the strong scaffolding between which the telescope could be moved in a perpendicular direction by means of several ropes, AE, FE; the horizontal motion of the whole apparatus, scaffolding and tube, was produced by a rotation by means of rollers running upon the periphery of a horizontal circular railway. ABAB. Around and above the whole was built a round tower with a revolving roof, whose opening could be brought towards the part of the heavens to be observed. More recently Lord Rosse has constructed a gigantic telescope, more than 12 feet longer than that of Herschel, having a speculum of 6 feet in diameter.
The Mural Quadrant
83. As long as astronomical observations did not possess that degree of accuracy now exhibited, the mural quadrant was, of all instruments used in measuring altitudes, the most useful. Pl. 15, fig. 19, represents the celebrated mural quadrant of Tycho. This had a radius, DC, of eight feet, by means of which, aided by a vernier, E, very small arcs could be read off on the limb CC. The iron grating, DCC, which formed the body of the quadrant, was fastened to a wall, GAA, placed in the meridian, and the rule DD, with the telescope, moved up and down on this grating. In this manner it was possible to observe not only the passage of the meridian by a star, but also its altitude or zenith distance. The depending plumb-line, DA, served to fix the quadrant in its proper position in the vertical plane.
Movable quadrants were also used; and the constructions of Dollond and Troughton (fig. 18) were the most convenient. The principal part consisted of the quarter circle. EF, and two attached radii, IE and IF, perpendicular to each other, all of metal. Through the centre of gravity of the movable part of the whole instrument, passed a cylindrical tube, fastened to the quadrant IFKE, and including the axis of rotation; this gave off a vertical post resting on a solid base, AAD, adjustable in a horizontal plane by the screws B, B, B. This post was received in such a manner into a tube, C, fastened to the base, as always, in rotation, to preserve a vertical position. The body of the quadrant was united in such a manner to this part containing the axis of rotation, as to have its plane constantly vertical, and parallel to the axis of rotation. Upon the part containing the axis of rotation was attached the azimuth circle, DD′, graduated to ten minutes, readable to ten seconds by means of a vernier. The quadrant, divided to five minutes, was readable to single seconds by the micrometer, G. The quadrant, with the movable telescope, KL, was so placed that one of the above mentioned metal radii was rendered perfectly horizontal by means of an attached level. H was a lens for reading off the graduation. Finally, as another means of determining the vertical position, a plumb-line was suspended in the above mentioned tube of the axis of rotation, whose proper position was given by four microscopes. K was the position occupied by the observer when looking at the stars through the telescope KL.
The Transit Instrument, or Meridian Telescope
84. The transit instrument, one of the most important instruments of practical astronomy, was invented by Roemer in 1706. It is intended to obtain with greater accuracy the right ascension of a star, and consequently the solar time. It consists (pl. 15, fig. 13) of an astronomical telescope, FD, fastened at right angles to a horizontal axis, B, and movable up and down in such a manner that the plane described always lies in the plane of the meridian of the place of observation. For the sake of the greatest possible firmness, the pillars, A A, upon which the two pivots of the horizontal axes rest, must be fixed separately, each one consisting of a single block of granite, and going deep into the earth, without any communication with the masonry of the building.
Portable transit instruments have also been constructed, differing, however, from the fixed only in their smaller size and their being adjustable to any point. Pl. 15, fig. 22, represents such a portable transit instrument. Although the transit instrument is not usually employed to obtain the meridian altitude of a star, yet for the approximate attainment of this end, a circle graduated to numbers is fastened to one side of the instrument in a vertical plane, as at I in fig. 13, and D, fig. 22.
In the fixed, heavy transit instruments, it is absolutely necessary, for the purpose of lessening the friction, and the wearing of the pivots, to diminish as much as possible the weight resting on the beds of the horizontal axis: this is done by counterpoises, as seen at H, H (fig. 13), L, L (fig. 11), and G, G (fig. 3). These act on one arm of levers whose fulcra are supported by the solid parts of the instrument, the other arms carrying stirrups through which the axis is received, so that this latter just touches the socket in which its pivots turn.
In the interior of the telescope, at the focus of the eye-glass, is the wire plate of fine threads of wire or other material, of which two are horizontal and an indefinite number vertical. The object here is to give greater precision to observation, by dividing the field of view into a certain number of subdivisions. This wire plate can be so moved as to be brought accurately into focus, and there regulated; to render it visible, however, it must be illuminated from without. This is done by making one half of the axis hollow, and reflecting the light of a lamp through this cavity into a hole in the side of the tube of the telescope. By this means, the cross lines are dark on a light ground. The illumination employed by Fraunhofer is, however, much more convenient; this is applied between the eye of the observer and the focus. Here the whole field of the telescope remains dark, the cross lines alone being illuminated, so that object and cross lines can be distinctly seen at the same time. As much depends upon the perfectly horizontal position of the axis of the instrument, it becomes necessary to apply frequently a test of this, which is done by a tubular level placed above or below, as in pl. 15, fig. 13, L. In the portable transit instrument (pl. 15, fig. 22), the stand, AABBCC, consists of a cast iron crown, upon which the two parts for the axis are immovably fastened. The horizontal position of the instrument is controlled in one direction by a level placed upon the axis; in the other, by a level, F, placed upon the declination circle, D.
The rectification of an astronomical instrument, or the determination of its faults, must precede its use. Three principal errors may attach to the transit instrument: in the first place, it will almost always deviate from the meridian, that is, it will have a small eastern or western azimuth; in the second place, it will almost always be inclined at a small angle to the plane of the horizon, which is determined by the dependent level, L (fig. 13); thirdly, the optical axis of the telescope will deviate at a slight angle from the line drawn perpendicular to the axis of rotation: this last error is called the error of collimation. These three errors must be ascertained and rectified, partly mechanically, and partly by calculation; as also the four errors to which the diaphragm or wire plate is generally subject.
Fig. 25 is a side, and fig. 31 a back view of a small transit instrument constructed by Repsold for the observatory of St. Petersburgh. A are the pillars of the axis G, fastened to a granite block: the pieces in which the pivots of the axis turn, are shown more in detail by figs. 26 and 27. E is the declination circle with its vernier, F, and the level, I, situated above the axis. The telescope, BD, is only partly given. At D is the adjusting screw for the ocular, given more in detail by figs. 28 and 29. Its micrometer arrangement is shown in fig. 30, where the wire plate is moved in the box, b, by the screw a. Fig. 32 is one of two supports which stand in excavations of the two pillars, A, carrying friction rollers above, upon which the axis G rests. Fig. 34 is a handle for directing the telescope.
Circular Instruments
85. As the irregularities produced by changes of temperature, eccentricity, specific gravity, &c., are greater in a part of a circle than in an entire one, it follows that even the most perfect quadrants do not afford the greatest possible degree of accuracy; for this reason full circles were introduced, now used almost exclusively in the determination of altitudes, and to which the remarkable precision of the astronomical observations of the present day is owing. To the circular instruments belong: 1, the repeating circle; 2, the simple circle; 3, the meridian circle; and 4, the theodolite.
86. The repeating circle of Dollond (fig. 14), intended for observations out of the meridian, rests upon a tripod stand, A A, which, by means of the adjusting screws, and the level F, can be made perfectly level. Upon this rests the horizontal circle, B, on which the direction of the alidade, H, can be accurately read off by means of four verniers provided with lenses: of these, only D and E are visible. The alidade H, which supports the four posts, I, I, I, I, of the full circle, is adjusted by the telescope T. The posts carry the beds for the horizontal axis of rotation of the two circles, O and L, and the principal telescope, M, whose horizontal position is regulated by the level attached to the strips K, K. The main telescope, M, has an adjustable ocular, provided with a micrometer arrangement. This telescope is fastened to the vernier carrier, PQ, which then determines altitudes in the fixed circle, O. The manner in which the repetition or multiplication is effected will be understood by referring to what has been said in the part of the work relating to measuring instruments (p. 65). We will here only remark, that for this purpose the vernier carrier, PQ, is fastened to the axis by clamps, which can be loosened in repeating. Reichenbach has very much improved the repeating circle; nevertheless, as there are always defects in the instrument, attention is now turned almost exclusively to simple fixed circles.
The Meridian Circles
87. The most prominent and costly instrument of modern practice astronomy, is incontestably the meridian circle, another kind of full circle, used to determine the altitudes of stars. This instrument serves not only to observe in the most accurate manner the culmination of the stars (as in the transit instrument), but also their zenith or polar distance. The entire instrument must therefore be set up in such a manner that its horizontal axis of rotation shall lie accurately in an east and west direction. The planes also of the two circles perpendicular to this axis, as well as the optical axis of the telescope, must be in the plane of the meridian. The meridian circle has much the same construction of the individual parts that is found in the transit instrument, as also the same errors and corrections. To the latter is to be added the verification by the observed altitude or polar distance of the star. The best meridian circles of an earlier date are those of Ramsden (particularly the one at Palermo) and of Troughton (at Leipzig). Perhaps the most perfect of more modern construction are those made by Reichenbach, and especially by the brothers Repsold in Hamburg.
In the meridian circle erected at the Hamburg observatory in 1836, its constructors, A. and G. Repsold, sought to solve the problem of avoiding every error arising from flexion, by the greatest equality and counter-balancing of the individual parts. For this reason the instrument is symmetrical in all its parts, the axis, BB (pl. 15, fig. 11), being bored within as well as without; two circles, F, F, of equal weight, with the accompanying microscope carriers, burden equally the axis, BB, and require equally heavy counterpoises, L, L, on both sides. To avoid a possible alteration of the axis, the attachment is very near the telescope, and a corresponding counterpoise on the other side restores the equilibrium of the whole. The circles are of cast brass, 3 feet 2 inches (French) in diameter, graduated on silver for every 2 minutes. These circles have four verniers, by which the angles can be read off to single seconds by lenses, R, R, fastened to the microscope carrier, FF. The massive centre, B (pl. 15, fig. 12), of this microscope carrier, itself composed of hollow tubes for the purpose of measuring absolute heights, is fitted to the axis in such a manner as to move freely without great friction in the boxes. The telescope (fig. 11), CE, with a Fraunhofer object glass, C, of 5 feet focus, consists of two equally heavy conical tubes, CB, BE, of hammered brass, which, firmly united to the axis BB, admit of no bending. The illumination of the cross lines is effected through the hollow axis by a mirror in the tube, a lamp being placed in one of the tubes running out in the prolongation of the axis. The obscuration, as also the regulation of the illumination, is quickly effected by a wedge of colored glass worked by a rack. The beds of the axis, entirely independent of the other parts of the instrument, are screwed fast to blocks of brass in the pillars, A, A′, behind which are the brass plates which support the posts, M, K, for the counterpoises L, L.
88. The meridian circle at the central observatory of Pulkowa (St. Petersburg), also erected by the brothers Repsold, is very similar to the preceding, though on a larger scale. Fig. 3, pl. 15, represents it in perspective. The two pillars, A and A′, are of grey granite, 7\(\frac{3}{5}\) feet high, and 18 inches broad each way at the upper end. The telescope, CB, has a focal length of 83\(\frac{1}{5}\) inches, 5\(\frac{4}{5}\) inch aperture of objective, and possesses magnifying powers of 170, 238, and 245. The wire plate in the focus at C, consists of two horizontal and nine vertical wires. Each of the two circles, BKEK and BK′E′, has a diameter of 48 inches, and is divided on silver to two minutes. For the counterbalancing, the counterpoises, G and G′, are attached to special metal posts, I, H and I′, H′. The whole instrument can be raised at F and F′. The level N rests on the cross piece M. Fig. 4 exhibits the microscope carrier on a larger scale. This consists of the hoop EE; the four microscopes themselves are at K, K, K, K; LL and L′L′ are the two levels, whose end views are given immediately to the left hand, with their mode of attachment; d, d, d, d, e, e, e, e, are the spokes; c, c and T, T are hollow tubes. Fig. 5a is a front view of the eye-piece of the telescope, CB (fig. 3); the letters a, b, c, f, g, h, in figs. 5a, 5b, indicate the separate parts of the wire micrometer, and d the pin for its adjustment; c (fig. 5b) is the separate tube of the ocular. Fig. 6 shows the construction of one of the four microscopes, K, attached to the microscope carrier; figs. 7, 8, 9, and 10, represent particular parts of the micrometer arrangement. Fig. 7 is the inner, fig. 8 the outer plate; fig. 9 the spindle of the micrometer screw h; and fig. 10 the external view of the whole micrometer arrangement from above.
The Equatorial
89. The Equatorial is an instrument by means of which, not only the declination, but also the difference of right ascension of a star and the zenith can be ascertained. Some idea of the instrument may be obtained by supposing an altitude circle so arranged, that the axis of rotation, previously vertical or perpendicular to the plane of the horizon, shall be perpendicular to the equator; in other words, that this axis placed in the meridian shall form an angle with the horizon equal to the height of the pole at the place of observation. Thus, in the altitude and azimuth instrument, the axis of rotation moves towards the zenith; in the equatorial, towards the pole of the equator. Its axis thus becomes parallel to that of the earth, and the azimuth circle of the simple circle becomes an hour circle, and the altitude circle a circle of declination. This instrument, when very accurately constructed and adjusted, possesses the exceedingly important advantage of giving, out of the meridian, the same determinations which the meridian circle affords at the moment of culmination alone.
The equatorial, as at present constructed, rests upon a prismatic stand. In the smaller portable instruments, however, the middle of the polar axis, I (fig. 15, which represents the one constructed by Repsold for the Hamburg observatory), rests upon a vertical brass pillar, A, with three feet; LMN is the hour circle, figured more intelligibly in fig. 17, with its micrometer arrangement, N, and the counterpoise, K. GHF (fig. 15) is the declination circle; C, D, K, the counterpoises for diminishing the friction; and OP the movable telescope. A very minute division of the hour circle is, strictly speaking, not necessary, as the exact determination of the right ascension is obtained in another manner. Fig. 16 shows the external and internal construction of the axis, EH, of the declination circle, GHF. In a well constructed equatorial—1, the axis of rotation must lie in the plane of the meridian, and 2. must form an angle with the horizon equal to the altitude of the pole at the place; 3, the plane of the declination circle must be parallel both to the axis of rotation and to the optical axis of the telescope.
The stands of the greater equatorials consist of a solid pyramidical base similar to that of the Dorpat refractor. One of this character, for example, is to be found in Munich, with a telescope of 8 feet focus and 6 inches aperture; the hour circle has a diameter of 9 inches, graduated to 4 seconds of time; and the declination circle, a diameter of 12 inches, divided to arcs of 10 seconds. The telescope, admitting a magnifying power of 400, follows, by means of a clock with a centrifugal pendulum, the diurnal motion of the stars.
The Theodolite
90. Another instrument to be noticed in this place is the Theodolite. Fig. 35 represents a lateral, fig. 36 an edge, and fig. 37 a superior view of a Theodolite constructed by Ertel of Munich. In the three views the same letters refer to the same parts. It rests upon a tripod stand, A A, with three adjusting screws, of which only two, B, B, are represented. On this tripod is a short column, C, and upon this column is placed the horizontal circle E, graduated to degrees, &c. Upon this, and turning on its centre, the standards, H, H, rotate. These carry at their extremities, pivot holes for the horizontal axis of the telescope, N, whose optical axis moves in a vertical plane. The whole arrangement is similar to that of a transit instrument, with this difference, that the Theodolite has a very finely graduated vertical circle for measuring altitudes, while the horizontal circle, E, is intended to measure horizontal angles, which are read oft' by the lenses, G. This horizontal circle, E, can be fastened or loosened at pleasure by the clamp arrangement, Fabb. K, K, are lenses or microscopes for reading off the vertical angles measured on the circle L, and M is the level required for rectifying the station of the instrument.
Theodolites are divided into two principal kinds — Compensating and Repeating Theodolites; they are also provided sometimes with a so-called rectifying telescope. As regards the use of the instrument, we would refer to what has been said of it in the mathematical portion of the work.
The errors and rectifications of the Theodolite are much the same as those of the meridian and transit instruments (sections 84 and 87). In conclusion, it may be remarked, that for the Theodolite may be substituted a repeating circle, a simple circle, or an universal instrument, as constructed by Ertel of Munich, and A. and G. Repsold in Hamburg. These instruments fulfil the aim of the Theodolite just as well, and even more completely; at least this is the case as far as regards astronomical observations.
The Reflecting Sextant; the Reflecting Sector; the Triquetrum
91. All the instruments already mentioned, as used for measuring angles, require an immovably vertical or horizontal position. This, however, cannot always be attained, in which case reflecting instruments are employed, which, by their constructions, compensate for the want of a fixed station. Among these be long first the reflecting sextant. This consists of a circular sector, amounting to from 60–65 degrees, and is an instrument of great value on land, but absolutely indispensable at sea. As, however, from the theory of the instrument, the angle indicated on the sextant is exactly half the true angular distance, every degree of the sector indicates two degrees of angular distance. The instrument, therefore, measures angles of 120° to 130°, on which account every half degree of graduation is marked as a whole degree. About the centre of the sector rotates an alidade, which carries a large plane mirror, passing through the centre of the sector; another somewhat smaller plane mirror is fixed perpendicularly to the plane of the sextant, and so adjusted, that when the alidade is brought to the zero point of the graduation, the planes of the two mirrors are parallel. This plane mirror is uncovered in its upper half, and in practice, the signal of one leg of the angle to be measured is seen by direct light, that of the other immediately under it by reflection. At the back part of the sextant, a handle of wood is attached, by which it is held during observation. Between the two mirrors are hinged variously colored glasses for the protection of the eyes when observing in a bright light. The astronomical telescope is screwed in such a manner into the frame that the objective end lies next to the mirror. The alidade carries a vernier with a lens for reading off the degrees. The sextant must not be too heavy, as it is to be held in the hand when in use. Sextants of greater dimensions, as of 8 inches radius and more, have stands specially adapted to them.
The errors of such an instrument must be ascertained before using it. The first of these is the error of collimation; the second, a want of parallelism of the axis of the telescope with the plane of the instrument; the third consists in an unequal distinctness of the direct and reflected image of the same object. The fourth error is when the sides of the mirrors are not accurately plane and parallel to each other; and the fifth has reference to the same circumstance in the colored glasses. All these errors must therefore be rectified before the instrument can be used.
The first application of the sextant is in measuring the angle between two objects at any direction with respect to the horizon. Here the least illuminated object is selected as the one to be seen by direct light. The second application is to the measurement of altitudes. To determine the altitude of an object by means of the sextant, look directly through the telescope at the image of the object in the horizon, which may either be a natural or an artificial one ; bring the plane of the sextant into the vertical position, and move the alidade until the reflected image of the object covers its direct image: the angular position of the alidade will indicate double the altitude desired.
Pl. 15, fig. 23, gives a perspective view of another form of sextant with a glass prism, of simpler form and less expensive construction. ABB is the body, BB the graduated limb, C the movable alidade with the vernier, D the lens for reading off the graduation, GF the telescope, E the box containing the prism, in which the two images must be brought in contact; the index will then give the angular distance of the two objects at the station of the observer. In this instrument the colored glasses are wanting.
92. Another kind of reflecting instrument formerly used in measuring angles of moderate value, is the Reflecting Sector (fig. 24), whose limb, DD, only contains somewhere from 10–15 degrees. The alidade carries the vernier E, with the double tangent screw, FF, for fine adjustment; I and K are the mirrors, GH the telescope with the bent ocular, H, so that the observer at H looks downwards into the telescope. At the present time the instrument is no longer used, owing to the difficulty of rectifying it. Even the reflecting sextant is but rarely employed on land, theodolites having taken its place, being equally convenient to carry when of small size, and giving angles with much greater precision. At sea, however, the sextant retains full sway, as there no other observing instrument can supplant it.
93. This is the appropriate place to refer to the triquetrum (fig. 21), an ancient instrument, supposed to have been invented by Ptolemy, for determining altitudes and amplitudes of the heavenly bodies. It consisted of a staff, A, placed vertically by the assistance of a plummet, D. Attached to this staff were two others, B and C, movable on hinges, and thus capable of forming various triangles with the first. On one of them, namely on B, were placed the sight vanes, a and b. The construction and use of the triquetrum (so called from its triangular shape) depended upon correct geometrical principles, although, as is very evident, observations made with it could be of but very superficial character.
The Sun-Dial; the Gnomon
94. Sun-dials are instruments by means of which the true solar time can be determined, when the sun is above the horizon and not obscured by clouds. Before the invention of wheel clocks, they formed the only means for an accurate determination of time. Gnomonics, a special department of applied mathematics, teaches the mode of constructing sun-dials on any plane or curved surface. Even the Egyptians were acquainted with the sun-dial; at least, Josephus expressly asserts that the obelisks served for astronomical observations; and Augustus caused an Egyptian obelisk to be erected in Rome for the same purpose. The Jews had them 732 b.c.; and as to their existence among the Greeks, they are to be found in the choragic monument of Andronicus Cyrrhestes in Athens. Papirius Cursor constructed the first sun-dial at Rome 290 b.c. Portable sun-dials were invented by Pope Sylvester in the tenth century.
Sun-dials consist generally of a face of proper form—the dial surface—upon which is an hour ring; on this latter, the shadow of a style or gnomon indicates the hours.
There are various constructions of dials, depending upon the position and character of the dial face. The simplest form, and the one most usually employed, is the equinoctial or equatorial dial, whose plane is parallel to the plane of the equator. In this form the hour ring forms a circle divided into 24 hours. The shadow of a style erected perpendicularly to the centre of the dial face, indicates the hours whenever the twelve o’clock line of the dial is fixed in the meridian of the place, and the style rendered parallel to the axis of the earth. This equatorial dial can of course be employed to determine the 24 hours in those countries only where the sphere is parallel, or which have the pole in their zenith. In our latitude only the half circle can be used, and that only from vernal to autumnal equinox.
When the plane of the dial is parallel to the plane of the horizon, it becomes a horizontal dial. The meridian line of this dial must be in the meridian of the place, and the index in the direction of the pole. To construct a horizontal dial, draw the line of six o’clock, and, perpendicular to this and bisecting it, the meridian, or twelve o'clock line. At the point of intersection draw a line, forming, with the six o’clock line, an angle equal to the altitude of the pole, or the latitude of the place. Taking a moderate length on this line as hypothenuse, complete the right-angled triangle, by letting fall from its extremity a perpendicular on the six o’clock line. From the intersections of the first mentioned lines as centres, and with the hypothenuse, and that part of the six o’clock line belonging to this right-angled triangle, as radii, describe two semicircles on the six o’clock line. Divide each into twelve equal parts, and from each point of division of the inner semicircle, draw lines parallel to the meridian ; and from each point of the outer semicircle, lines parallel to the six o'clock line. Through the intersection of these two sets of parallels, prolong radii of the semicircles. These latter radii, twelve in number, will be the lines of shadow cast by the edge of the style for the 12 hours intervening between 6 a.m. and 6 p.m.: when produced on the other side of the centre, they will indicate the hours from 6 p.m. to 6 a.m. Thus, 7 a.m. produced, will indicate 7 p.m., &c. The outline of the dial plane may be square or circular. The style of the dial must form, with its plane, an angle equal to the altitude of the pole at the place of erection. If the style have an appreciable thickness of material, it will be necessary in the construction to suppose the semicircle divided into quadrants, and these separated by a parallel-sided space, equal in breadth to the thickness of the style. Since a simple index post is easily bent and moved from the required angle, it is preferable to employ a right-angled triangle, whose hypothenuse forms with the base an angle equal to the altitude of the pole.
95. When the surface of the dial is in a vertical plane, it becomes a vertical dial, of which there are four forms, named after and corresponding to the four principal regions of the heavens: morning (oriental), noon (azimuthal), evening (occidental), and midnight dials, as the vertical planes are turned towards the east, south, west, or north. These dials may be constructed mechanically by means of an equatorial dial and the rays of the sun.
The surface of the dial need not necessarily be turned to any particular part of the heavens, nor be exactly horizontal or perpendicular, although the construction of these declining dials becomes more difficult, and requires a greater knowledge of mathematics. Polar dials are those traced on a plane perpendicular to the meridian, and passing through the poles; the index is here parallel to the equator. There are also cylindrical dials where the surface is a cylinder; and annular, where the hour circle is marked on the inside of a ring. The rays of the sun falling through a hole in a hoop upon this circle, determine the hours. The portable dials are principally horizontal, and must be set up by means of a compass.
It remains to remark, in conclusion, that as the sun-dials indicate only the true, and watches the mean time alone, the two can only agree exactly twice in the year.
96. The Gnomon was a contrivance of the ancients, to determine the altitude of a luminous body above the horizon, by the shadow cast by a vertical style upon a horizontal plane. Anaximander made use of the gnomon to determine approximately the obliquity of the ecliptic at 24°; and after that, Pythias and Hipparchus calculated the solstices and altitudes of the sun. In all probability the obelisks of the Egyptians were nothing else than such gnomons, by means of which they obtained the culmination of the sun. and consequently the true noon, for the purpose of regulating their water clocks. An improvement of this apparatus is presented by the Thread Gnomon, in which the solar rays are received on a vertical wall perpendicular to the plane of the meridian, and the precise position of the meridian plane, passing through the centre of a circular aperture in the wall, indicated by a depending thread. It will be readily understood that the meridian lines required for each gnomon must be previously determined with the greatest possible degree of accuracy.
The Wheel Clock
97. By the word clock, without further qualification, is meant every machine which, by means of the perfectly uniform motion of wheelwork, is intended to divide mean, solar, or sidereal time, into a certain number of equal parts; the minuteness and accuracy of these latter depending on the more or less complete elaboration of the component parts of the apparatus.
It is an ascertained fact that the first clocks were moved by weights. Galileo and Huyghens first applied the pendulum to regulate the motion of the clock by its regular oscillations. In the sixteenth century a spiral spring was used as a motive power instead of the weights, and the pendulum was replaced by the balance wheel. By means of these two substitutions, it became possible to reduce the mechanism of the clock within so small a compass, as to render it sufficiently portable for pocket use; and although the honor may be contested against him, Peter Hele of Nürnberg is to be considered as the inventor of watches.
98. This is not the place to go into a minute description of the mechanism of a clock; it must be remarked, however, that the motive power, whether bent spring or weight, acts upon a wheel with a certain number of teeth, and that by a proper arrangement of wheels and pinions, the indices are moved in such a manner that the one (the minute hand) makes twelve rotations while the other (the hour hand) makes but one. There is often a third index (the second hand) which makes one rotation in a minute. In the better clocks the second hand springs from one second to another, thus showing each one separately; and as in astronomical clocks minute divisions of time are desirable, in these the division of seconds has sometimes been brought to thirds.
As the motive power can never act uniformly, every clock requires a regulator, which may compensate for the irregularities of the power. The whole wheelwork is consequently in such connexion with a single wheel—the escapement, that when the latter is checked the motion of the whole stops. This escapement, in the pendulum clock, is connected with the pendulum, which vibrates either whole or half seconds; the motion ceases, therefore, between every swing of the pendulum. It is thus seen that the proper motion of the clock depends upon the accurate length of the pendulum, and that as pendulums swing in proportion to their lengths, a clock may be regulated by lengthening or shortening the pendulum. The pendulum itself, however, needs regulating; for, being lengthened by heat and shortened by cold, the correctness of the clock’s motion is impaired. As it is not possible always to determine this variation of length, and the variation is often very sudden, it cannot be provided for by any manual regulation. To meet this difficulty Harrison invented a compensation pendulum which regulates itself. In this pendulum, rods of brass and steel alternate in such a manner, that the elongation of the steel rods, and consequently of the pendulum, is counteracted by that of the brass rods, which in this manner shorten the pendulum as much as it is lengthened by the steel rods. Its length thus remains unchanged in all temperatures. Graham’s mercurial pendulum is intended to accomplish the same end. (For further details see the article, Compensation Pendulum, under the head of Physics.)
In the second kind of regulators, all the wheels are connected with the balance wheel by means of the escapement, so that this produces the necessary check to the motion. Of escapements there are various forms, all, however, being in connexion with a balance, which is a flat wheel, on whose pallets the scape wheel catches, endeavoring to move it forwards. The pallets are so fixed on the verge of the balance wheel, that the scape wheel must leave them free after a certain time, and then the spiral spring acts upon the balance, bringing it back to the former position to meet a new tooth of the escapement. It will be readily seen that the quicker or slower motion of a clock will depend upon the time in which the balance makes its movement, and that this time depends upon the length or shortness of the spiral spring. There is for this reason a regulator on the watch whose motion alters the length of the spring.
As in the pendulum isochronism of oscillation is effected by the principle of compensation, so in the balance there must also be a compensation, since both it and the spiral spring change their dimensions, and consequently their times of vibration, with change of temperature. Compensation is brought about in the balance by the bending of thermometric metal springs, steel and brass, or platina plates, being so combined that their changes through temperature counterbalance those which, for the same reason, take place in the balance.
99. Clocks for astronomical purposes must be very carefully constructed, and every tendency to inaccuracy must be specially counteracted. They may be pendulum clocks, as used in observatories, or balance clocks—chronometers—as employed at sea to assist in the astronomical determinations there necessary. The English, to whom the perfection of chronometers is due, set great value upon the best of them, and Harrison furnished instruments which, in a voyage round the world, did not vary three seconds. Such chronometers are little different in construction from the best watches, except in having a peculiar escapement; all their parts are, however, very carefully constructed, many precautions taken against accidental injury, and throughout, compensations for the effects of temperature and other physical agents (as magnetism) introduced. Longitude or marine time keepers (box chronometers) for nautical and astronomical purposes, are constructed just like the pocket chronometers ; they are, however, larger, and inclosed in a special box.
The Planetarium
100. Among the numerous helps to the study of astronomy and mathematical geography, must be mentioned those artificial models and contrivances known under the names of Lunarium, Tellurium, and Planetarium. The lunarium is an apparatus by which the motions of the moon about the earth, her phases, &c., can be readily illustrated and explained. It is usually combined with the tellurium. The tellurium, called sometimes geocyclic machine, is a particular form of planetarium, which exhibits the motion of the earth round the sun, the course of the moon about the earth, and with her about the sun, as also all attendant phenomena, such as the seasons, quarters of the moon, &c. Finally, the planetarium is a model, intended to render perceptible to the senses the motions of the planets and all resulting phenomena, on which account it has received various constructions. Common planetaria are moved by hand; the better and more complicated have a wheelwork, which, like a watch, is set in motion by a spiral spring, and causes the planets to revolve with their respective velocities around a globe or lamp placed in the centre. As Lord Orrery was the first to construct a planetarium of this character, they are sometimes known as Orreries.
Henderson, formerly director of the Edinburgh observatory, has published the description of a simplified planetarium (pl. 15, fig. 38), whose construction will be here briefly mentioned. In a circular box standing on four feet, the clockwork is set in motion by the handle D. Upon the upper surface of the box are marked the ecliptic, the perpetual calendar, and other items relating to the planets. In the centre is a large sphere representing the sun, about which the planets revolve on vertical posts fastened to horizontal rods, with their proportional velocities, and at their proportional distances—Mercury, H; Venus, G; Earth, F, with the moon, c; Mars, I; Jupiter, M, with four moons, e, e, e, e; Saturn, N, with the ring, and the seven satellites, f, f, f, f, f, f, f; as also Uranus, K, with the six moons, d, d, d, d, d, d. Fig. 39 represents a contrivance, which, attached to this planetarium, serves to give the earth’s axis a parallel motion, and to exhibit the cause of the seasons and their succession. It consists of the small globe, F, to whose equator the hollow brass tube, E, is fastened, which carries the weight, C, and the carrier, D. If now the planetarium be hung to the wall by the ring E (fig. 38), and set in motion, C being held fast, the earth will revolve, her axis remaining constantly parallel, and thus representing the courses of the seasons, which are indicated on the fixed disk, A.
The best Planetaria and Telluria are those of Riedig and Schulze in Leipzig, and Seifert of Hohenstein near Chemnitz in Saxony.
101. It remains to mention, in conclusion, that there are still other pieces of apparatus, some of them ancient, and others more modern, which are used with excellent results both by the practical astronomer and the teacher. Among these may be mentioned the circle micrometer, as also the differential micrometer (invented by Boguslawski) for determining the difference of right ascension and declination of two stars: the dipleidoscope (invented by Dent of London), an apparatus which replaces the transit instrument; the beautiful model by Möbius of Leipzig, for representing the orbits of the asteroids, Ceres, Pallas, Juno, and Vesta, with respect to their magnitudes, inclinations, and eccentricities; finally, the mercurial clock of Kater, and the astrograph of Steinheil.
Observatories
102. The place where astronomical observations are conducted and the necessary apparatus erected, is called an observatory. The choice of such a place is sometimes very much restricted; where this is not the case, it should, be established in a dry locality, where, remote from all motion which might produce vibrations, the foundations and lower stones of the buildings and the instruments may be protected from the influences of weather and temperature. The building itself must be constructed in the most solid manner, and, if possible, facing the four quarters of the heavens. It is desirable to have an elevated station from which the horizon can be surveyed in every direction; where this is impossible, the parts of the building in which are placed the principal instruments must be much elevated. The foundations of the edifice must be very solid, and each principal instrument must have an isolated base, or must be connected with the ground by special foundations, not touching any part of the edifice, in order that all shaking of the instrument may be avoided. A free view in all directions must be had, and for the meridian there must be a vertical slit passing through the whole height of the building. The place also where the refractor, or other instrument supplying its place, stands, must be so arranged that the whole of a vertical plane can be seen in any direction, for which reason there is generally a roof attached which turns on a railroad, or can be entirely removed. In the first case, the roof is divided by a vertical section of four feet in breadth, into two halves; the aperture, however, can be closed by trap-doors. Such an arrangement, for example, is to be found in the building for the great refractor at Dorpat, and in the turning cupola of the observatory at Washington.
The best observatories are those at Altona, Berlin, Dorpat, Göttingen, Greenwich, Königsburg, Mailand, Munich, Ofen, Pulkowa near St. Petersburg, Seeberg near Gotha, Vienna, &c. In the other parts of the world, those at the Cape of Good Hope, Paramatta in New South Wales, and in the United States, are the best known. In the United States, the principal observatories and instruments are at Cambridge, Philadelphia, Washington, Cincinnati, Hudson (O.), &c.
Practical Astrognosy
103. The finding of particular stars and constellations is effected by means of the celestial globe and star maps; as also by the method of alignments already mentioned (sec. 26). This latter method will now be detailed a little more at length. It was there seen that from the position of the Great Wain, or the Great Bear, the polar star could be determined; and in the same manner other stars are identified. For this the star maps (pl. 12) are employed, on which the alignments of the principal fixed stars are given. Produce the direction of the stars ζ and η towards the wain, it will strike a star of the first magnitude, Arcturus in Bootes, which, with the polar star and Vega in Lyra, forms an isosceles triangle, Arcturus being at the vertex. The polar star, which, by its almost unchangeable position, is very well calculated for the purpose, serves as a point of departure for the rest of the heavens; the altitude of the polar star above the horizon being nearly equal to the geographical latitude of the place. Twice the length of a straight line from Vega to Arcturus strikes Spica, a star of the first magnitude in Virgo. Spica forms, with Denebola (in Leo) and Arcturus, and also with Arcturus and the star α Libræ, triangles nearly isosceles. Spica forms the vertex of the first of these; Arcturus of the second. The star α Libræ lies almost in the continuation of the connecting line between the polar star and Arcturus. Furthermore, the alignments of Vega, the polar star, Capella, and Aldebaran, form a large flat arc. Aldebaran, a star of reddish light, is one of five stars lying near to each other, which form a V, and are called Hyades. Aldebaran and Capella form an almost right-angled triangle with Castor, a star in Gemini. A line drawn from Denebola to the polar star, and produced some distance beyond, strikes a bright star, which, with three others, forms a large almost regular quadrilateral, the greater part of Pegasus. A line from Perseus to Aldebaran, and sufficiently prolonged, strikes three bright stars, the belt of Orion. Produce the line indicated by this belt to the left, and it will meet the brightest star in the sky, Sirius (the Dog star). In this manner, straight lines may in succession be drawn from two known stars to others, and the triangles thus formed, constructed in the heavens.
104. With the help of a celestial globe, the same end may be attained more readily, by setting up the sphere for the place of observation, as also for the day and hour of observation. It is then only necessary to look in what direction and at what elevation above the horizon any star is found on the globe, and then direct the eye towards the corresponding part of the heavens, to be able to identify them on both spheres. In this way, for instance, it might be observed by means of the celestial globe, that at 7\(\frac{1}{2}\) o’clock of Jan. 18, a star of the first magnitude, Capella, stands a little to the south-east of zenith, outside of the milky way. It is then only necessary at that time to look a little to the south-east, out of the milky way, actually to see Capella.
105. Knowing the twelve constellations of the zodiac, it will not be difficult to find the visible planets, Mercury, Venus, Mars, Jupiter, Saturn, and even Uranus, in these constellations, distinguishing them with certainty from the fixed stars by their peculiar appearance and their varying position with respect to the neighboring stars.